Weak temporal signals can synchronize and accelerate the transition dynamics of biopolymers under tension
- PMID: 22908254
- PMCID: PMC3437832
- DOI: 10.1073/pnas.1202952109
Weak temporal signals can synchronize and accelerate the transition dynamics of biopolymers under tension
Abstract
In addition to thermal noise, which is essential to promote conformational transitions in biopolymers, the cellular environment is replete with a spectrum of athermal fluctuations that are produced from a plethora of active processes. To understand the effect of athermal noise on biological processes, we studied how a small oscillatory force affects the thermally induced folding and unfolding transition of an RNA hairpin, whose response to constant tension had been investigated extensively in both theory and experiments. Strikingly, our molecular simulations performed under overdamped condition show that even at a high (low) tension that renders the hairpin (un)folding improbable, a weak external oscillatory force at a certain frequency can synchronously enhance the transition dynamics of RNA hairpin and increase the mean transition rate. Furthermore, the RNA dynamics can still discriminate a signal with resonance frequency even when the signal is mixed among other signals with nonresonant frequencies. In fact, our computational demonstration of thermally induced resonance in RNA hairpin dynamics is a direct realization of the phenomena called stochastic resonance and resonant activation. Our study, amenable to experimental tests using optical tweezers, is of great significance to the folding of biopolymers in vivo that are subject to the broad spectrum of cellular noises.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 [or
[or  ] calculated from the tilted 1D free energy profile interpolated from results of the SOP model displays a good agreement with other results. (C) Mean folding time [τF(f)] and unfolding time [τU(f)] at varying tensions, obtained from the SOP simulation (circles),
] calculated from the tilted 1D free energy profile interpolated from results of the SOP model displays a good agreement with other results. (C) Mean folding time [τF(f)] and unfolding time [τU(f)] at varying tensions, obtained from the SOP simulation (circles), and
and  obtained from the 1D simulation on the tilted free energy profile (squares), and mean first passage times (
obtained from the 1D simulation on the tilted free energy profile (squares), and mean first passage times ( ,
,  calculated using the tilted free energy profile (solidcurves) are in a good agreement. The transition midforce determined at the intersection between τF(f) and τU(f) and is fm = 14.7 pN.
calculated using the tilted free energy profile (solidcurves) are in a good agreement. The transition midforce determined at the intersection between τF(f) and τU(f) and is fm = 14.7 pN.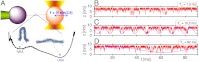
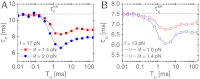
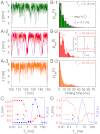
 , as shown in (A- 2). The inset in (B- 2) depicts the power spectrum S(ν), showing the sharpest peak at ν = 1/TSR ≈ 0.1 ms-1. (C) Mean folding time τF and measure of coherence P1 as a function of TΩ. (D) Mean unfolding time τU and measure of coherence P1 as a function of TΩ with f = 13 pN and δf = 1.4 pN. Note that the SR and RA conditions are made at different TΩs in C and D.
, as shown in (A- 2). The inset in (B- 2) depicts the power spectrum S(ν), showing the sharpest peak at ν = 1/TSR ≈ 0.1 ms-1. (C) Mean folding time τF and measure of coherence P1 as a function of TΩ. (D) Mean unfolding time τU and measure of coherence P1 as a function of TΩ with f = 13 pN and δf = 1.4 pN. Note that the SR and RA conditions are made at different TΩs in C and D.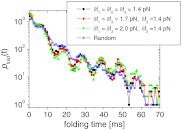
 at varying combinations of δfi with Ω1 = 2π/0.1 ms-1, Ω2 = 2π/10 ms-1, Ω3 = 2π/100 ms-1, and f = 17 pN. For filled symbols, we fix δf2 = 1.4 pN, corresponding to the amplitude for the optimal frequency Ω2 for SR, and vary the other amplitudes to be δf1 = δf3 = 1.4 pN (filled squares), 1.7 pN (filled circles), and 2.0 pN (filled triangles), respectively. The starred symbols represent the cases where δf1, δf2 and δf3 are taken randomly between 0 and 2 pN every time step to make a nonequilibrium noise δf(t). Notably, the folding transition filters the optimal driving period despite other drivings with larger or transient amplitudes.
at varying combinations of δfi with Ω1 = 2π/0.1 ms-1, Ω2 = 2π/10 ms-1, Ω3 = 2π/100 ms-1, and f = 17 pN. For filled symbols, we fix δf2 = 1.4 pN, corresponding to the amplitude for the optimal frequency Ω2 for SR, and vary the other amplitudes to be δf1 = δf3 = 1.4 pN (filled squares), 1.7 pN (filled circles), and 2.0 pN (filled triangles), respectively. The starred symbols represent the cases where δf1, δf2 and δf3 are taken randomly between 0 and 2 pN every time step to make a nonequilibrium noise δf(t). Notably, the folding transition filters the optimal driving period despite other drivings with larger or transient amplitudes.Similar articles
-
Refolding dynamics of stretched biopolymers upon force quench.Proc Natl Acad Sci U S A. 2009 Dec 1;106(48):20288-93. doi: 10.1073/pnas.0905764106. Epub 2009 Nov 13. Proc Natl Acad Sci U S A. 2009. PMID: 19915145 Free PMC article.
-
Temperature-driven coherence resonance and stochastic resonance in a thermochemical system.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Feb;89(2):022916. doi: 10.1103/PhysRevE.89.022916. Epub 2014 Feb 18. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25353554
-
Stretching dynamics of semiflexible polymers.Eur Phys J E Soft Matter. 2007 Aug;23(4):375-88. doi: 10.1140/epje/i2006-10221-y. Epub 2007 Aug 29. Eur Phys J E Soft Matter. 2007. PMID: 17728980
-
Using photoinduced charge transfer reactions to study conformational dynamics of biopolymers at the single-molecule level.Curr Pharm Biotechnol. 2004 Jun;5(3):285-98. doi: 10.2174/1389201043376896. Curr Pharm Biotechnol. 2004. PMID: 15180550 Review.
-
Probing conformational dynamics in biomolecules via chemical exchange saturation transfer: a primer.J Biomol NMR. 2017 Apr;67(4):243-271. doi: 10.1007/s10858-017-0099-4. Epub 2017 Mar 19. J Biomol NMR. 2017. PMID: 28317074 Review.
Cited by
-
Talin folding as the tuning fork of cellular mechanotransduction.Proc Natl Acad Sci U S A. 2020 Sep 1;117(35):21346-21353. doi: 10.1073/pnas.2004091117. Epub 2020 Aug 17. Proc Natl Acad Sci U S A. 2020. PMID: 32817549 Free PMC article.
-
Stochastic resonance during a polymer translocation process.J Chem Phys. 2016 Apr 14;144(14):144901. doi: 10.1063/1.4945559. J Chem Phys. 2016. PMID: 27083746 Free PMC article.
-
Thermal and inertial resonances in DNA unzipping.Eur Phys J E Soft Matter. 2015 May;38(5):126. doi: 10.1140/epje/i2015-15041-4. Epub 2015 May 22. Eur Phys J E Soft Matter. 2015. PMID: 25990632
-
T-cell Receptor Is a Threshold Detector: Sub- and Supra-Threshold Stochastic Resonance in TCR-MHC Clusters on the Cell Surface.Entropy (Basel). 2022 Mar 10;24(3):389. doi: 10.3390/e24030389. Entropy (Basel). 2022. PMID: 35327900 Free PMC article. Review.
References
-
- Alberts B, et al. Molecular Biology of the Cell. 5th Ed. New York: Garland Science; 2008.
-
- Kim JS, Backman V, Szleifer I. Crowding-induced structural alterations of random-loop chromosome model. Phys Rev Lett. 2011;106:168102. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

