Bifurcations of Periodic Solutions of a Hamiltonian System with a Discrete Symmetry Group | Programming and Computer Software
Skip to main content
Springer Nature Link
Log in

Bifurcations of Periodic Solutions of a Hamiltonian System with a Discrete Symmetry Group

  • Published:
Programming and Computer Software Aims and scope Submit manuscript

Abstract

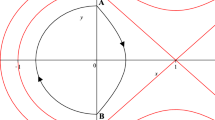
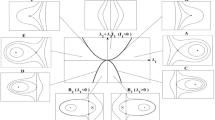
An autonomous Hamiltonian system with two degrees of freedom that is invariant under the Klein four-group of linear canonical automorphisms of the extended phase space of the system is studied. A sequence of symplectic transformations of the monodromy matrix of the symmetric periodic solution of this system is constructed. Using these transformations, the structure and bifurcation of the phase flow in the vicinity of this solution is investigated. It is shown that the bifurcations corresponding to the multiple period increase are different for the solutions with double symmetry and the solutions with a single symmetry. An example of critical periodic solutions of the family of doubly symmetric orbits of the plane circular Hill problem is discussed. The majority of tedious analytical calculations are performed using packages for the computation of Gröbner bases and for the work with polynomial ideals in the computer algebra system Maple.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

REFERENCES

  1. Barrio, R. and Blesa, F., Systematic search of symmetric periodic orbits in 2DOF Hamiltonian systems, Chaos, Solitons Fractals, 2009, vol. 41, no 2, pp. 560–582.

    Article  MathSciNet  Google Scholar 

  2. Jorba, A. and Zou, M., A software package for the numerical integration of ODE by means of high order Taylor methods, Preprint, 2004, p. 32.

  3. Abad, A., Barrio, R., Blesa, F., and Rodríguez, M., Algorithm 924: TIDES, a Taylor series integrator for differential equations, ACM Trans. Math. Software, 2012. vol. 39, no. 1, Article No. 5.

    Article  MathSciNet  Google Scholar 

  4. Thompson, I., Understanding Maple, Cambridge Univ. Press, 2016.

    MATH  Google Scholar 

  5. Meurer, A, Smith, C.P., Paprocki, M., et al., SymPy: Symbolic computing in Python, Peer J. Comput. Sci., 2017, vol. 3, p. e103. https://doi.org/10.7717/peerjcs.103

    Article  Google Scholar 

  6. Wolfram, S., The Mathematica Book, Wolfram Media, Inc., 2003.

    MATH  Google Scholar 

  7. Batkhin, A.B., Some properties of doubly symmetric periodic solutions to Hamiltonian system, Int. Conf. on Polynomial Computer Algebra, St. Petersburg, 2019, Vassiliev, N.N., Ed., St. Petersburg: Euler International Mathematical Institute., 2019, pp. 25–28.

  8. Batkhin, A.B., Bifurcations of periodic solutions to the Hamilton system with discrete symmetries, Proc. of the Int. Conf. on Computer Algebra, Moscow, 2019, Abramov, S.A. and Sevast’yanov, L.A., Eds., Moscow: Ross. Univ. Druzhby Narodov, 2019, pp. 90–97.

  9. Batkhin, A.B., On the structure of phase flow in the neighborhood of the symmetric periodic solution of the Hamilton system, Preprint of the Keldysh Inst. of Applied Mathematics, Russ. Acad. Sci., Moscow, 2019, no. 69.

  10. Lamb, J.S.W. and Roberts, J.A.G. Time-reversal symmetry in dynamical systems: A survey, Physica D, 1998, vol. 112, pp. 1–39.

    Article  MathSciNet  Google Scholar 

  11. Meyer, K.R., Periodic Solutions of the N-body Problem, Lecture Notes in Mathematics, vol. 1719, Berlin: Springer, 1999.

  12. Hénon, M., Generating Families in the Restricted Three-Body Problem, Lecture Note in Physics, Monograph no. 52, Berlin: Springer, 1997.

  13. Wintner, A. The Analytical Foundations of Celestial Mechanics, Princeton N.J.: Princeton Univ. Press, 1941.

    MATH  Google Scholar 

  14. Yakubovich, V.A. and Starzhinskii, V.M., Linear Differential Equations with Periodic Coefficients, Nauka: Moscow, 1972 [in Russian].

    Google Scholar 

  15. Markeev, A.P., Libration Points in Celestial Mechanics and Astrodynamics, Nauka: Moscow, 1978 [in Russian].

    Google Scholar 

  16. Poincaré, H., Les métods nouvelles de la mécanique céleste, Paris: Gauthier-Villars, 1893, vol. 1.

    Google Scholar 

  17. Kreisman, B.B., Families of periodic solutions to Hamiltonian systems: nonsymmetrical periodic solutions for a planar restricted three-body problem, Cosmic Res., 2005, vol. 43, no. 2, pp. 84–106.

    Article  Google Scholar 

  18. Holodniok, M, Klič, A., Kubiček, M., and Marek, M., Methods for the Analysis of Nonlinear Dynamical Models, Mir: Moscow, 1991 [in Russian].

  19. Gantmakher, F.R., The Theory of Matrices, New York: Chelsea, 1959).

  20. Williamson, J., On the normal forms of linear canonical transformations in dynamics, Am. J. Math., 1937, vol. 59, no. 3, pp. 599–617.

    Article  MathSciNet  Google Scholar 

  21. Bruno, A.D., The Restricted 3-Body Problem: Plane Periodic Orbits, Moscow: Nauka, 1990; New York: de Gruyter, 1994.

  22. Karimov, S.R. and Solo’skii, A.G. Parametric continuation method for natural families of periodic motions of Hamiltonian systems, Preprint of the Inst. of Theoretical Astronomy, Russ. Acad. Sci., Moscow, 1990, no. 9.

  23. Meyer, K.R. and Offin, D.C., Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, Applied Mathematical Sciences, vol. 90, 3rd ed., New York: Springer, 2017.

  24. Theory of Bifurcations, Arnold, V.I., Afraimovich, V.S., and Shil’nikov, L.P., Eds., Modern Problems of Mathematics. Fundamental Trends, vol. 5, VINITI Akad. Nauk SSSR, 1985.

  25. Batkhin, A.B. and Batkhina, N.V., Hill’s Problem, Volgograd: Volgogradskoe nauchnoe Izdatel’stvo, 2009 [in Russian].

  26. Szebehely, V., Theory of Orbits, the Restricted Problem of Three Bodies, New York: Academic, 1967.

    MATH  Google Scholar 

  27. Morales-Ruiz, J., Simó, C., and Simon, S. Algebraic proof of the non–integrability of Hill’s problem, Ergodic Theory Dynam. Syst., 2005, vol. 25, no. 4, pp. 1237–1256.

    Article  MathSciNet  Google Scholar 

  28. Batkhin, A.B., Symmetric periodic solutions of the Hill’s problem, Cosmic Res., 2013, vol. 51, no. 6, 452–464.

    Article  Google Scholar 

  29. Batkhin, A.B., Web of families of periodic orbits of the generalized Hill problem, Doklady Math., 2014, vol. 90, no. 2, pp. 539–544.

    Article  MathSciNet  Google Scholar 

  30. Hénon, M., Numerical exploration of the restricted problem. V. Hill’s case: Periodic orbits and their stability, Astron. & Astrophys., 1969, vol. 1, pp. 223–238.

    MATH  Google Scholar 

  31. Hénon, M., Numerical exploration of the restricted problem. VI. Hill’s case: Non-periodic orbits, Astron. & Astr., 1970, no. 9, pp. 24–36.

  32. Hénon, M., New families of periodic orbits in Hill’s problem of three bodies, Celest. Mech. Dyn. Astr., 2003, vol. 85, pp. 223–246.

    Article  MathSciNet  Google Scholar 

  33. Hénon, M., Families of asymmetric periodic orbits in Hill’s problem of three bodies, Celest. Mech. Dyn. Astr., 2005, vol. 93, pp. 87–100.

    Article  MathSciNet  Google Scholar 

Download references

ACKNOWLEDGMENTS

I am grateful to Prof. A.D. Bruno for his support and fruitful discussion of this work.

Author information

Authors and Affiliations

  1. Keldysh Institute of Applied Mathematics, Russian Academy of Sciences, 125047, Moscow, Russia

    A. B. Batkhin

  2. Moscow Institute of Physics and Technology, 141700, Dolgoprudnyi, Moscow oblast, Russia

    A. B. Batkhin

Authors
  1. A. B. Batkhin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. B. Batkhin.

Additional information

Translated by A. Klimontovich

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Batkhin, A.B. Bifurcations of Periodic Solutions of a Hamiltonian System with a Discrete Symmetry Group. Program Comput Soft 46, 84–97 (2020). https://doi.org/10.1134/S0361768820020036

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0361768820020036

Search

Navigation