Carotid Plaque Fibrous Cap Thickness Measurement by ARFI Variance of Acceleration: In Vivo Human Results - PMC Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Dec 1.
Published in final edited form as: IEEE Trans Med Imaging. 2020 Nov 30;39(12):4383–4390. doi: 10.1109/TMI.2020.3019184

Carotid Plaque Fibrous Cap Thickness Measurement by ARFI Variance of Acceleration: In Vivo Human Results

Gabriela Torres 1, Tomasz J Czernuszewicz 2, Jonathon W Homeister 3, Mark A Farber 4, Melissa C Caughey 5, Caterina M Gallippi 6
PMCID: PMC7725192  NIHMSID: NIHMS1650680  PMID: 32833633

Abstract

This study evaluates the performance of an acoustic radiation force impulse (ARFI)-based outcome parameter, the decadic logarithm of the variance of acceleration, or log(VoA), for measuring carotid fibrous cap thickness. Carotid plaque fibrous cap thickness measurement by log(VoA) was compared to that by ARFI peak displacement (PD) in patients undergoing clinically indicated carotid endarterectomy using a spatially-matched histological validation standard. Fibrous caps in parametric log(VoA) and PD images were automatically segmented using a custom clustering algorithm, and a pathologist with expertise in atherosclerosis hand-delineated fibrous caps in histology. Over 10 fibrous caps, log(VoA)-derived thickness was more strongly correlated to histological thickness than PD-derived thickness, with Pearson correlation values of 0.98 for log(VoA) compared to 0.89 for PD. The log(VoA)-derived cap thickness also had better agreement with histology-measured thickness, as assessed by the concordance correlation coefficient (0.95 versus 0.62), and, by Bland-Altman analysis, was more consistent than PD-derived fibrous cap thickness. These results suggest that ARFI log(VoA) enables improved discrimination of fibrous cap thickness relative to ARFI PD and further contributes to the growing body of evidence demonstrating ARFI’s overall relevance to delineating the structure and composition of carotid atherosclerotic plaque for stroke risk prediction.

Index Terms—: Atherosclerosis, carotid endarterectomy (CEA), carotid plaque, acoustic radiation force impulse (ARFI) imaging

I. Introduction

STROKE, a leading cause of morbidity and mortality in the United States and around the world, is predominantly ischemic secondary to a thromboembolic event [1]. Ischemic stroke often occurs subsequent to carotid atherosclerotic plaque rupture, so properly identifying rupture-prone carotid plaque is vitally important to stratifying stroke risk [2]. The features of rupture-prone, or ‘vulnerable’, plaques are well described and include thin fibrous cap, large lipid-rich necrotic core, increased vasa-vasorum neovascularization, inflammation, and intra-plaque hemorrhage [3–6]. Among these features, thin fibrous cap conveys the highest hazard ratio (HR) for stroke (intraplaque hemorrhage HR = 4.59 versus necrotic core HR = 3.00) [4]. Therefore, technologies that support accurate measurement of fibrous cap thickness could substantially improve stroke risk assessment and facilitate optimal disease management.

While the relevance of fibrous cap thickness to stroke risk prediction is well known, it is absent from current clinical diagnostic algorithms. The conventional method for evaluating carotid plaque is duplex ultrasound, which estimates stroke risk by Doppler-derived blood flow velocity and degree of stenosis [7]. Because its assessment of stroke risk is based on degree of stenosis, duplex underestimates risk in the case of positive vascular remodeling. Moreover, it is incapable of determining plaque composition and structure, including fibrous cap thickness [8].

Alternatives to duplex are emerging, including MRI [9–11], optical techniques based on optical coherence tomography [12, 13] and optical spectroscopy [14, 15], virtual histology [16, 17], and elastographic methods, all of which aim to evaluate the composition and structure of carotid atherosclerotic plaque. Elastographic approaches evaluate plaque composition and structure by interrogating mechanical properties deduced from tissue displacement in response to intrinsic or extrinsic mechanical excitations. For example, in response to intrinsic arterial pulsation, Roy-Cardinal et al developed a plaque component classification scheme that uses homodyned-K parametric maps and elastograms to identify ruptured fibrous cap with an AUC of 0.97 [18, 19]. Further, Hansen et al demonstrated compound ultrasound strain imaging methods for identifying fibrous plaques [20] and Schaar et al and de Korte et al demonstrated intravascular elastography for characterizing plaque components [21, 22]. In addition, Nayek et al have developed methods for estimating carotid artery strain using synthetic aperture imaging [23, 24].

Using Acoustic Radiation Force Impulse (ARFI) imaging, Czernuszewicz et al demonstrated ARFI-induced peak displacement (PD) for measuring fibrous cap thickness [25]. In 25 patients undergoing clinically indicated carotid endarterectomy, carotid plaques were imaged in vivo immediately prior to surgery. Imaging results were interpreted by three trained, blinded readers, and the assessments were compared to an expert pathologist’s interpretation of the spatially matched histology of the extracted plaque specimens. The best reader outcomes for average fibrous cap thickness were in close correlation with the histologically measured thickness (R = 0.89), but Bland Altman analysis revealed a statistically significant positive bias of 0.12 ± 0.30 mm. Further, in silico studies by Czernuszewicz et al indicated that for the employed system parameters, the minimum measurable fibrous cap thickness was 0.2 mm, suggesting in vivo overestimation of fibrous cap thicknesses smaller than this level [26].

A likely cause of fibrous cap thickness overestimation by ARFI PD assessment is improper delineation of the boundaries between the lumen and the fibrous cap and between the fibrous cap and the underlying lipid-rich necrotic core (LRNC) or intraplaque hemorrhage (IPH). Therefore, a method for improving differentiation of fibrous cap boundaries could improve cap thickness measurement to support more accurate carotid plaque risk assessment. Rather than ARFI PD, a potential strategy is to employ an alternative ARFI-derived parameter, Variance of Acceleration (VoA), which has been demonstrated for differentiating subcutaneous hemorrhage from surrounding soft tissue [27] and for identifying carotid plaque composition and structure [28].

As its name implies, VoA is calculated as the variance of the second time-derivative of ARFI induced tissue displacement. The second time-derivative is a high-pass filtering operation that amplifies variance, or “jitter”, in the displacement estimate. Therefore, VoA is directly related to jitter magnitude (σ), which is derived from the Cramer-Rao lower bound [29] as,

σ≥32f3π2T(B3+12B)[1ρ2(1+1SNR2)2−1], (1)

where f is the center frequency, T is the tracking kernel size, B is the bandwidth, ρ is the correlation coefficient, and SNR is the signal to noise ratio. When the first three parameters, f, T, and B, are maintained constant, jitter magnitude varies specifically due to SNR and signal decorrelation in the region of analysis. Considering that signals will be more decorrelated and have lower SNR when they originate from luminal blood than from plaque fibrous cap, VoA is relevant to differentiating lumen-cap boundaries. Similarly, considering that signals will be more decorrelated and have lower SNR when they originate from soft, hypoechoic LRNC and IPH, VoA is relevant to discriminating cap-underlying plaque boundaries. In this study, we present the novel application of ARFI VoA to supporting more accurate and precise fibrous cap thickness measurement in human carotid plaque, in vivo, relative to ARFI PD. This hypothesis is herein tested using ARFI data previously acquired from patients undergoing clinically indicated carotid endarterectomy (CEA), with histological validation [25].

II. Methods

A. Patient Recruitment

Patient recruitment and imaging protocol are described in detail on our prior work [25]. A total of 25 patients undergoing clinically indicated CEA were recruited from UNC Hospitals. Inclusion criteria included either asymptomatic carotid artery disease with >60% Doppler-indicated stenosis and unresponsive to medical management or symptomatic carotid artery disease with a stenosis suspected to be the source of emboli. All procedures were approved by the institutional review board (IRB), and informed written consent was given from each study participant.

B. ARFI Imaging

A Siemens Acuson Antares research imaging system (Siemens Healthcare, Ultrasound Division) was used for in vivo imaging with a VF7–3 linear array transducer. ARFI excitation pulses were 300-cycles at 4.21 MHz, tracking pulses were 2-cycles at 6.15 MHz, and acquisitions were timed to diastole using electrocardiogram gating. From the acquired radio frequency data, ARFI-induced displacements were measured using normalized cross correlation (NCC) with a 1.5λ (376-μm) kernel, two-stage interpolation, and linear motion filtering [30].

A registered sonographer (M.C.C.) acquired all imaging data before patient sedation, on the same day of surgery. The time interval between imaging and specimen extraction was approximately four hours. The plaque to be removed by CEA was identified from prior ultrasound imaging sessions archived in the patient’s medical record and was typically the plaque with the greatest stenosis. Before completing the imaging session, the transducer was rotated 90°, and transverse B-modes and CINE loops of the carotid bifurcation were obtained to aid in sample alignment (see Section II-D below).

C. ARFI-Derived Parameter Estimation

ARFI PD and VoA parameters were calculated from ARFI-induced displacement versus time profiles. From the displacement profiles, which were obtained using one-dimensional (axial) normalized cross correlation [30], PD was calculated as the maximum displacement per pixel, as described in [31]. VoA was calculated as the unbiased variance of the second time derivative through the total ensemble time per pixel:

VoA(x,y,ti)=1k−1∑j=1i+(k−1)|Acc(x,y,tj)−μA(x,y,ti)|2, (2)

where x and y are axial and lateral pixel coordinates, respectively, t is ensemble time, k is the total number of ensemble time samples, Acc is acceleration, and μAcc is the mean of Acc.

D. Histology

CEA specimens were harvested, μCT imaged (Scanco 40, Scanco Medical AG, Bassersdorf, Switzerland), and processed for spatially-matched histological validation. Spatial alignment was performed by matching the histological cutting plane with the imaging frame using the μCT image as reference for orientation before paraffin embedding. The orientation and alignment process were performed by a separate reviewer, before and independent of the quantitative analysis described below. A more detailed description of the process for aligning ARFI and histology data is contained in Czernuszewicz et al [25].

The aligned microscopy images were divided into four laterally adjacent, equally sized subsections spatially corresponding to four laterally adjacent, equally sized quarters in the ARFI images. The histology subsections were read by a pathologist with expertise in atherosclerosis (J.W.H.), who hand-delineated fibrous caps using a custom graphical user interface (GUI) developed in Matlab (Mathworks Inc., Natick, MA, USA) for the previous blinded-reader study [25]. In the parametric ARFI image subsections, fibrous caps were segmented using a semiautomatic k-means clustering method [28, 32]. Centroids from each fibrous cap were calculated from the parametric images aligned with histology, and these centroids were input to the k-means algorithm for segmenting k regions, where k is the number of fibrous cap areas identified by the pathologist on each histology slide. A more detailed description of this clustering method is contained in Torres et al [28].

E. Data Analysis

Exclusion criteria were applied to the data collected from the 25 patients to ensure high-quality and well-matched histology and ARFI data. First, plaque specimens that were damaged or fractured during surgery were excluded. Second, plaques imaged with the lumen-plaque boundary outside the axial range of ARFI imaging (spanning ± 5 mm from the focal depth) were excluded. Third, carotid plaques without the presence of a fibrous cap in histology were excluded. After data exclusions, 14 fibrous caps were retained for comparison of fibrous cap thickness measurement by ARFI PD and VoA parameters.

ARFI PD and VoA outcomes were rendered into two-dimensional parametric images, with VoA depicted as its decadic logarithm, denoted log(VoA), to increase dynamic range. For display purposes, both PD and log(VoA) images were normalized to the mean value within the plaque ± two median absolute deviations (MAD). The linear relationship between histology-derived fibrous cap thickness measurements and imaging-derived thickness from PD and log(VoA) images were visually assessed in scatterplots and tested by Pearson correlation. Bland-Altman analysis was performed to evaluate the agreement between fibrous cap thicknesses derived from ARFI and histology. Finally, the concordance correlation coefficient (CCC), a measure of both the precision and accuracy of imaging-derived thickness compared to histology-derived thickness, was calculated for both ARFI PD and ARFI log(VoA), with the CCC closest to 1 considered to be the most accurate and precise measurement [33]. All statistical analyses were performed using Matlab (Mathworks Inc., Natick, MA, USA).

III. Results

For a representative plaque from a 53 year-old symptomatic female, B-Mode, ARFI PD, and ARFI log(VoA) images are shown in Figure 1, without (left column) and with (right column) the automatically segmented fibrous cap regions shown in white. The fibrous cap thicknesses derived from the segmented regions in PD and log(VoA) images were 0.93 and 0.90 mm, respectively, while the thickness of the fibrous cap hand-delineated by the pathologist was 0.84 mm. For reference, the plaque boundary hand-delineated from ARFI PD images by the best-performing radiologist reader in [25] is shown in black.

Fig. 1.

Fig. 1.

Open in a new tab

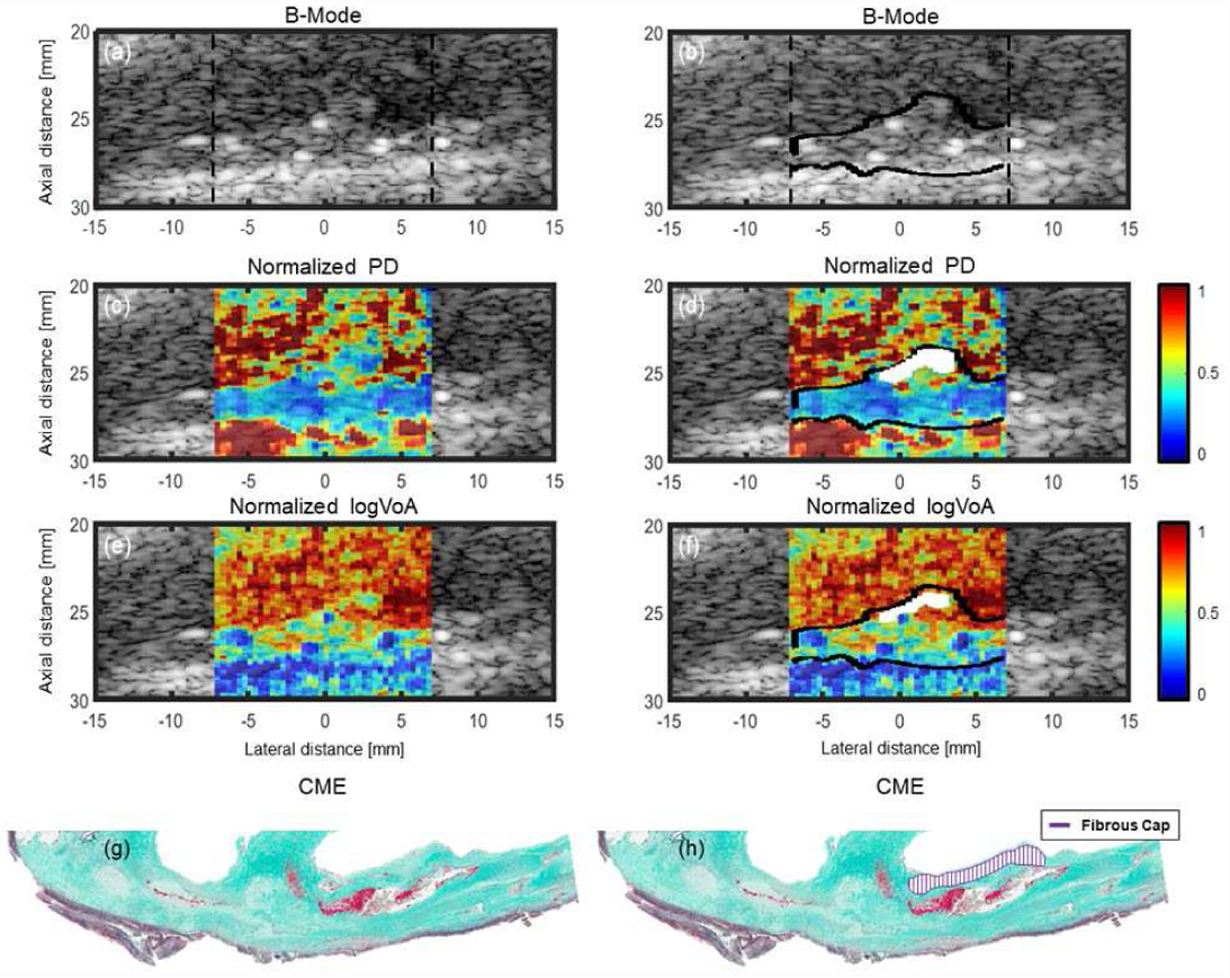
Carotid plaque ARFI images with matched histology in a symptomatic 53-year-old female. From top to bottom: B-mode (a, b), normalized ARFI PD image (c, d), and normalized ARFI log(VoA) image, (e, f), and CME stains (g, h). In (b), (d), and (f), the plaque boundary hand-delineated from ARFI PD images by the best performing radiologist reader in [25] is shown in black, and the fibrous caps automatically segmented from PD and log(VoA) images are shown in white. In (h), the fibrous cap outline hand-delineated by the pathologist is shown.

Figure 2 shows another carotid plaque example from a symptomatic 45-year-old female. Again, the automatically segmented fibrous caps are shown in white in the right column. These segmentations yielded fibrous cap thickness measures of 0.99 and 0.90 mm for ARFI PD and log(VoA), respectively, while the histology-derived thickness was 0.91 mm.

Fig. 2.

Fig. 2.

Open in a new tab

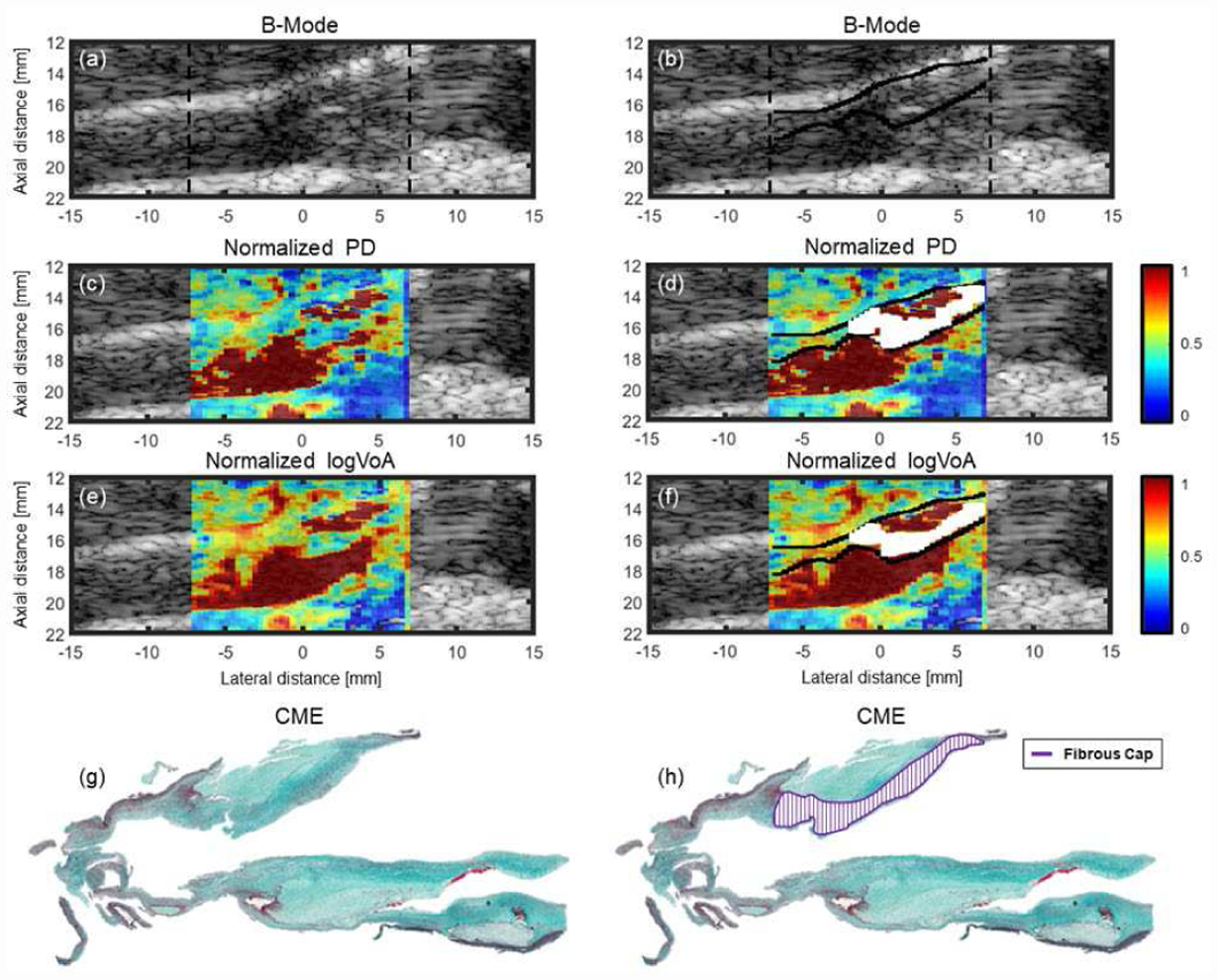
Carotid plaque ARFI images with matched histology in a symptomatic 45-year-old female. From top to bottom: B-mode (a, b), normalized ARFI PD image (c, d), and normalized ARFI log(VoA) image (e, f), and CME stains (g, h). In (b), (d), and (f), the plaque boundary hand-delineated from ARFI PD images by the best performing radiologist reader in [25] is shown in black, and the fibrous caps automatically segmented from PD and log(VoA) images are shown in white. In (h), the fibrous cap outline hand-delineated by the pathologist is shown.

Figure 3 shows a third plaque example from a symptomatic 59-year-old male. In this case, the fibrous cap thicknesses derived from automatic segmentation of PD and log(VoA) images were 1.40 and 1.35 mm, respectively, while the fibrous cap thickness measured from the spatially matched histology was 1.26 mm.

Fig. 3.

Fig. 3.

Open in a new tab

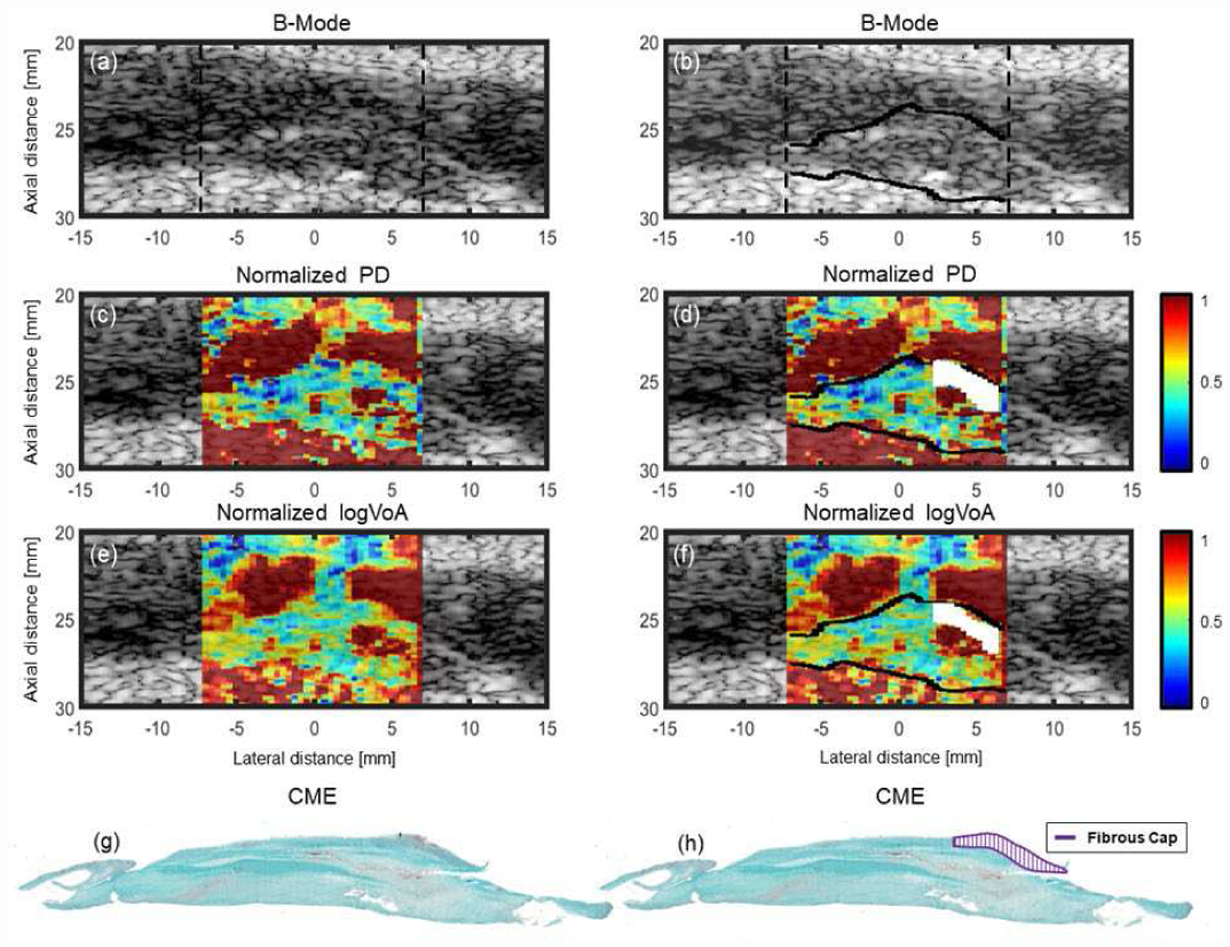
Carotid plaque ARFI images with matched histology in a symptomatic 59-year-old male. From top to bottom: B-mode (a, b), normalized ARFI PD image (c, d), and normalized ARFI log(VoA) image (e, f), and CME stains (g, h). In (b), (d), and (f), the plaque boundary hand-delineated from ARFI PD images by the best performing radiologist reader in [25] is shown in black, and the fibrous caps automatically segmented from PD and log(VoA) images are shown in white. In (h), the fibrous cap outline hand-delineated by the pathologist is shown.

Figure 4 illustrates median ARFI PD (a) and log(VoA) (b) fibrous cap thickness measurements plotted versus the histological validation standard for the evaluated plaques. It can be observed that median PD-derived fibrous cap thickness measurements correlated more weakly with the validation standard than corresponding log(VoA) measures. The R2, sum squared error (SSE) values were (0.79, 0.19) for PD and (0.97, 0.03) for log(VoA). The concordance correlation coefficient (CCC) was 0.62 for PD and 0.95 for log(VoA), which indicates more precision and agreement between log(VoA) and histology than PD and histology. Additionally, the correlation between histology with PD was 0.88 (95% CI: 0.38 to 0.90; P = 0.001), while the correlation with log(VoA) was stronger, at 0.98 (95% CI: 0.94 to 0.99, P<0.0001). In figure 5, Bland-Altman results indicate that the coefficient of variation was 16% for PD-derived median fibrous cap thickness versus 6.3% for log(VoA)-derived median fibrous cap thickness. The bias in PD-derived median fibrous cap thickness, 0.10 mm, was statistically significant, while the 0.05 mm bias in log(VoA)-derived median fibrous cap thickness was not statistically significant (p<0.05).

Fig. 4.

Fig. 4.

Open in a new tab

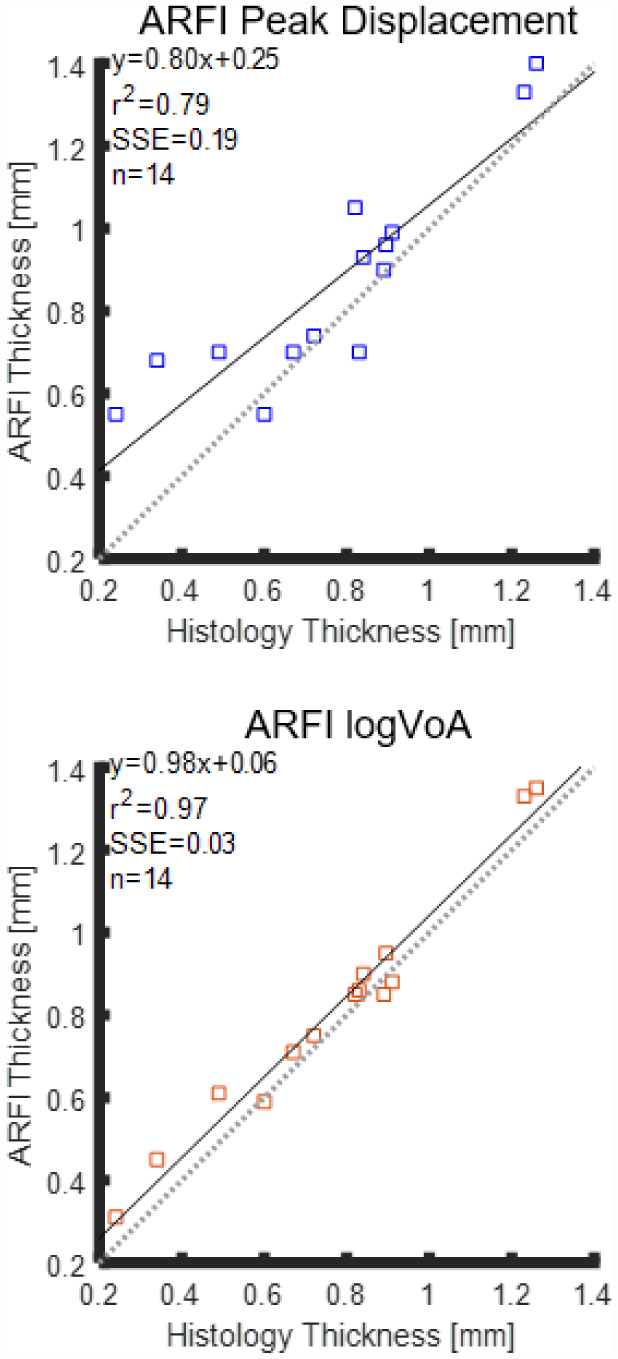
Linear regressions of ARFI PD- (top) and log(VoA)- (bottom) derived median fibrous cap thicknesses versus median histological standard over fourteen human carotid plaques, in vivo (black lines). Median values per plaque are shown as circular scatters. R2: coefficient of determination. SSE: Sum of squares error.

Fig. 5.

Fig. 5.

Open in a new tab

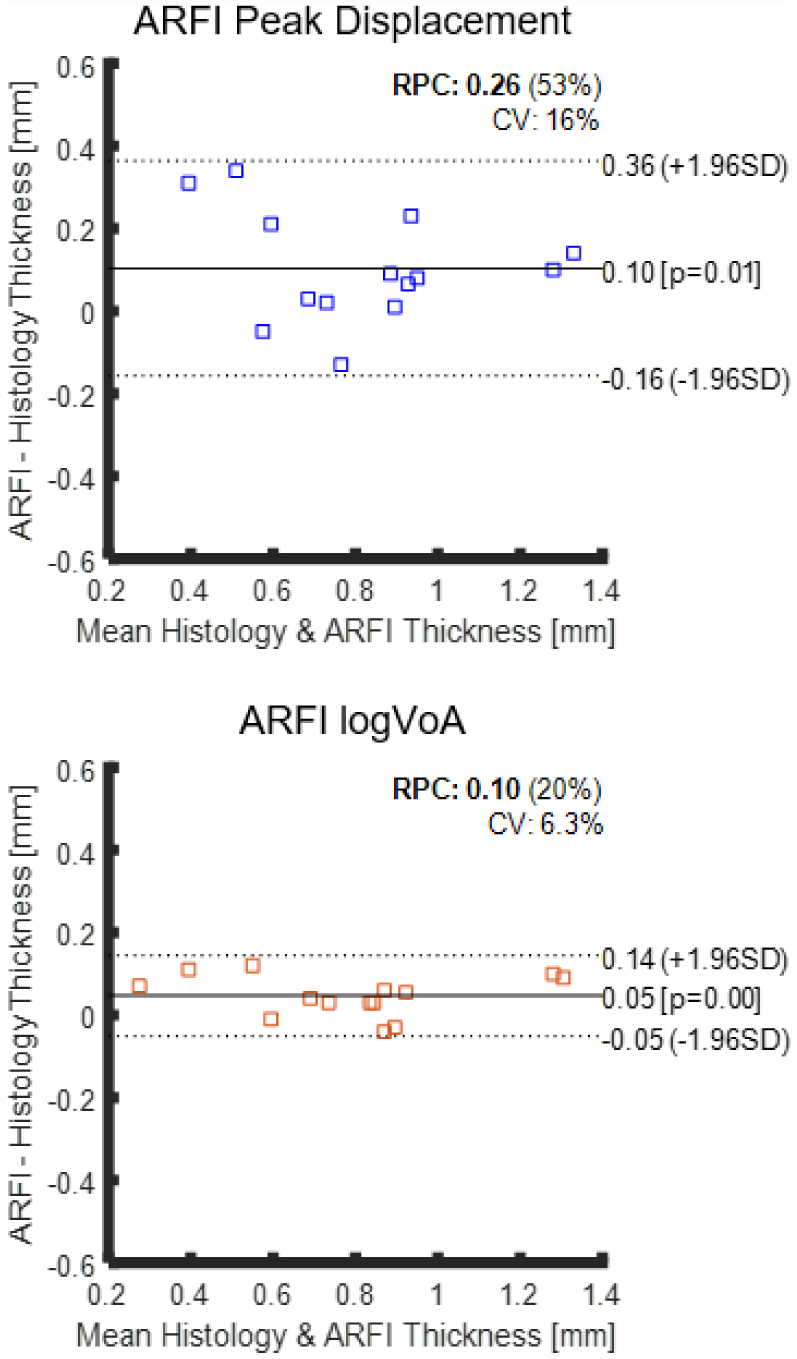
Bland-Altman plots assessing the reproducibility of median plaque thickness results derived from ARFI PD (top) and ARFI logVoA (bottom). RPC: Reproducibility coefficient, CV: Coefficient of variation.

Figure 6 illustrates minimum (a) PD and (b) log(VoA) fibrous cap thickness measurements plotted versus the histological validation standard. The (R2, SSE) values were (0.74, 0.22) for PD and (0.95, 0.05) for log(VoA). The concordance correlation coefficient (CCC) was 0.61 for PD and 0.87 for log(VoA). Figure 7 shows Bland-Altman results for the minimum fibrous cap thickness measurements. The coefficient of variation for minimum fibrous cap thickness measurement was 20% for PD versus 8.6% for log(VoA).

Fig. 6.

Fig. 6.

Open in a new tab

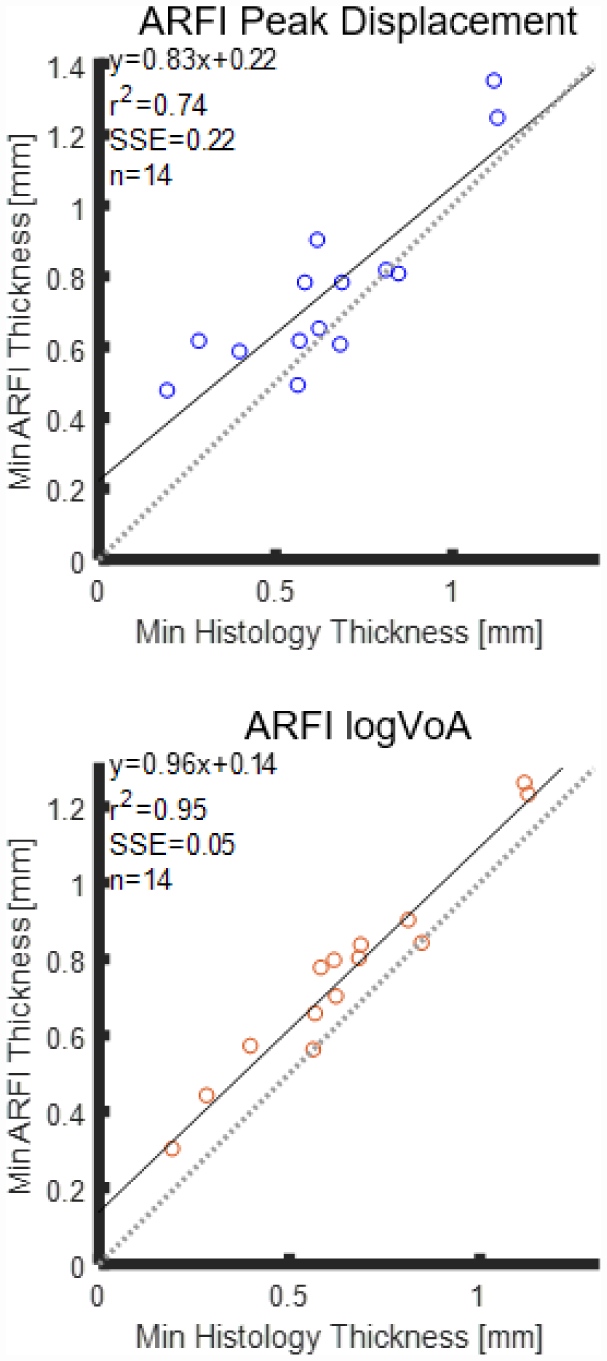
Linear regressions of ARFI PD- (top) and log(VoA)- (bottom) derived minimum fibrous cap thicknesses versus minimum histological standard over fourteen human carotid plaques, in vivo (black lines). Minimum values per plaque are shown as circular scatters. R2: coefficient of determination. SSE: Sum of squares error.

Fig. 7.

Fig. 7.

Open in a new tab

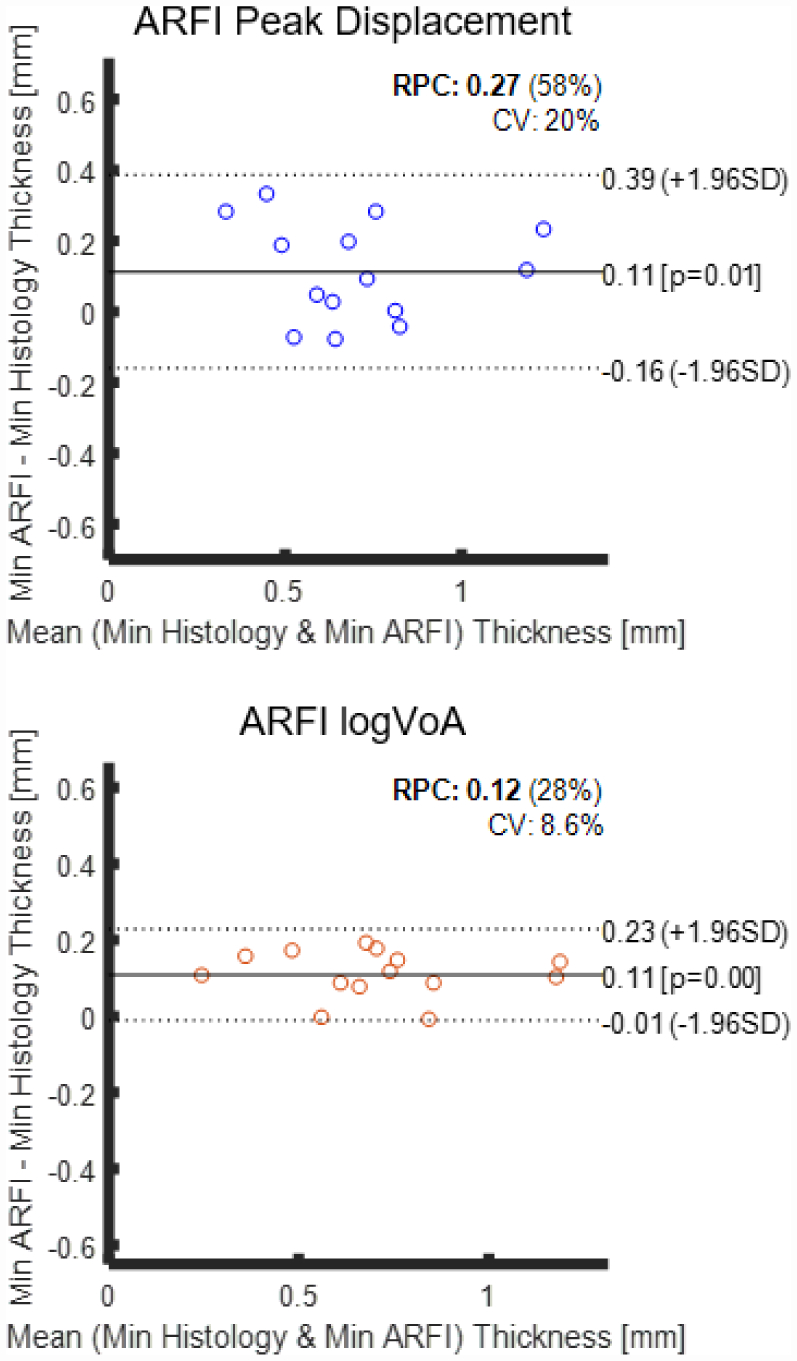
Bland-Altman plots assessing the reproducibility of minimum plaque thickness results derived from ARFI PD (top) and ARFI logVoA (bottom). RPC: Reproducibility coefficient, CV: Coefficient of variation.

Figure 8 illustrates maximum (a) PD (a) and (b) log(VoA) fibrous cap thickness measurements plotted versus the histological validation standard. For the maximum fibrous cap thickness measurements, the (R2, SSE) values were (0.67, 0.35) for PD and (0.84, 0.23) for log(VoA). The concordance correlation coefficient (CCC) was 0.55 for PD and 0.89 for log(VoA). Figures 9 shows Bland-Altman results for maximum fibrous cap thickness measurements. The coefficient of variation for maximum fibrous cap thickness measurement was 21% for PD versus 16% for log(VoA).

Fig. 8.

Fig. 8.

Open in a new tab

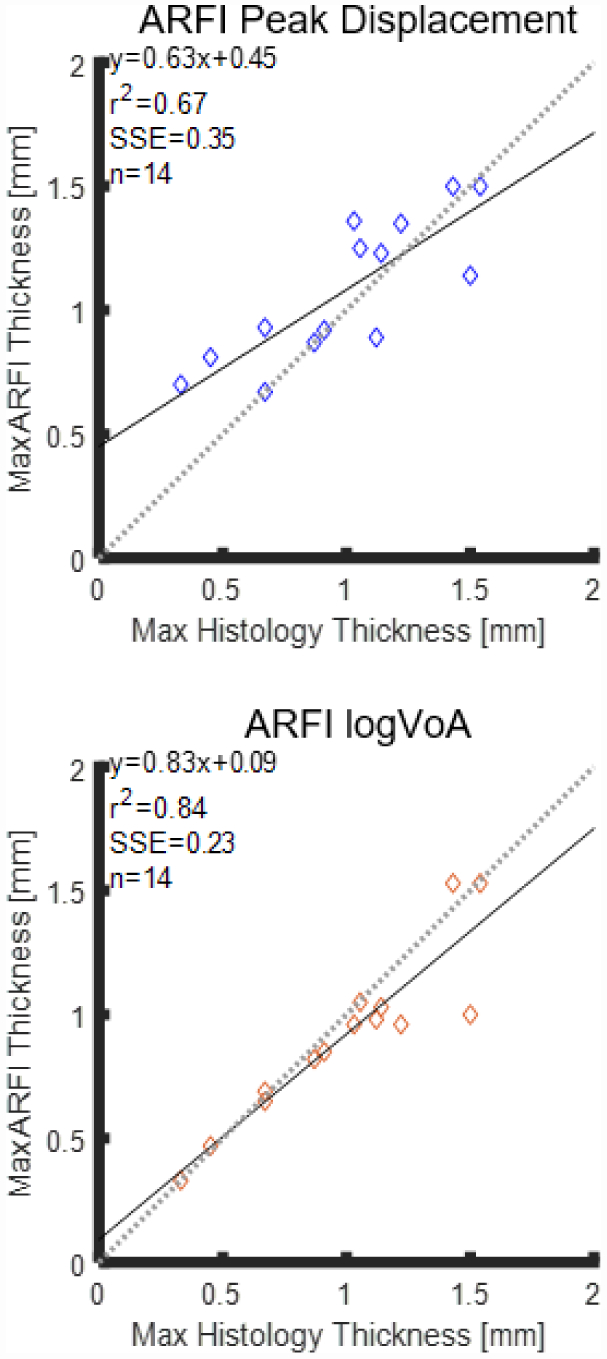
Linear regressions of ARFI PD- (top) and log(VoA)- (bottom) derived maximum fibrous cap thicknesses versus maximum histological standard over fourteen human carotid plaques, in vivo (black lines). Maximum values per plaque are shown as circular scatters. R2: coefficient of determination. SSE: Sum of squares error.

Fig. 9.

Fig. 9.

Open in a new tab

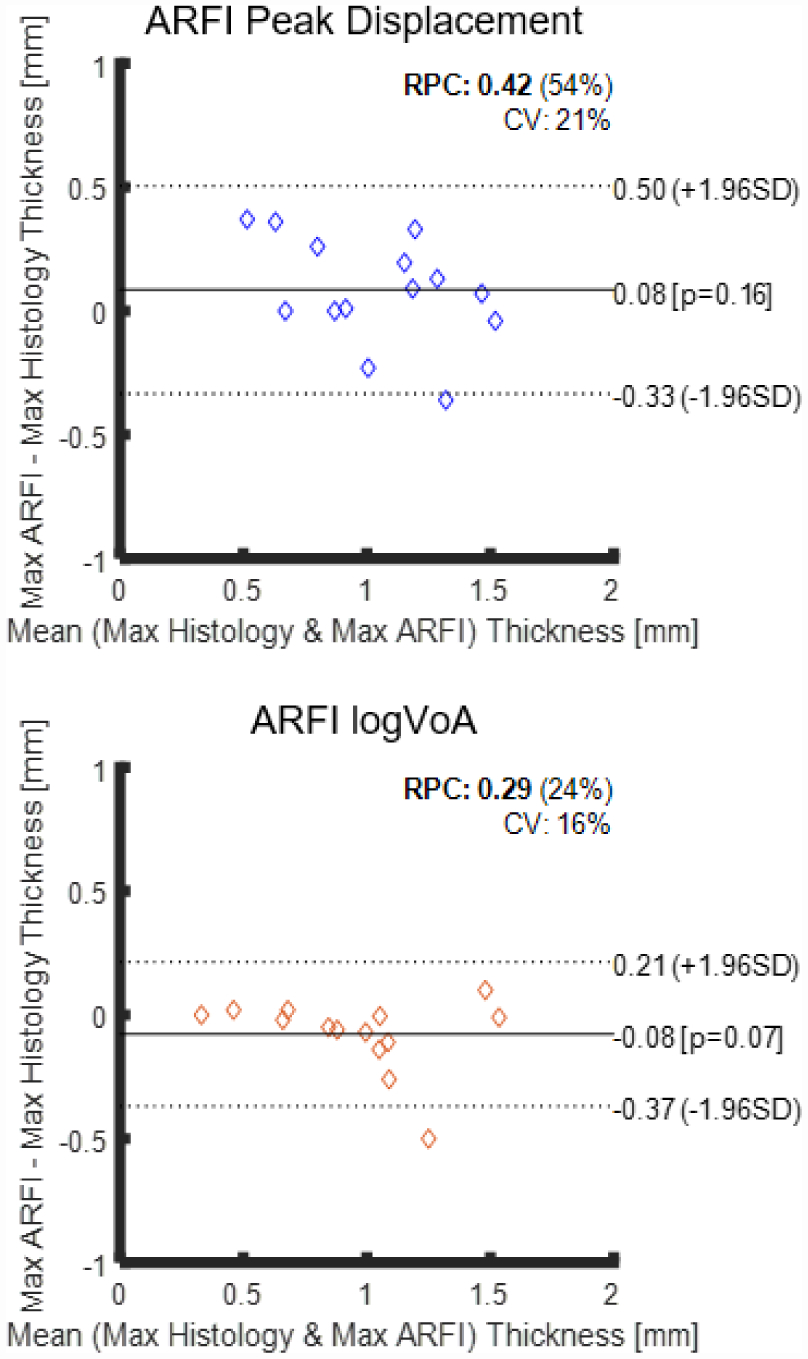
Bland-Altman plots assessing the reproducibility of maximum plaque thickness results derived from ARFI PD (top) and ARFI logVoA (bottom). RPC: Reproducibility coefficient, CV: Coefficient of variation.

The axial locations of PD- and log(VoA)-derived lumen-cap and cap-LRNC boundaries were compared. The median difference in {PD – log(VoA)} lumen-cap boundary position was −0.33 ± 0.21 mm. The median difference in {PD −log(VoA)} cap-LRNC boundary position was +0.21 ± 0.10 mm.

IV. Discussion

In Figure 1, the boundary using the ARFI PD image yields a median fibrous cap thickness measurement that is 10.71% larger than the histological validation standard, while the thickness derived using log(VoA) is 7.14% larger. These data, suggesting that median fibrous cap thickness measurement by log(VoA) is in better agreement with the histological validation standard than that by PD, are consistent with the results observed in Figure 2 (relative to histology, 8.79% larger median fibrous cap thickness by PD versus 1.10% larger by logVoA) and Figure 3 (relative to histology, 11.11% larger median fibrous cap thickness by PD versus 7.14% larger by logVoA). Over these plaques, median fibrous cap thickness measured by PD had an absolute difference of 0.10 ± 0.26 mm compared to histology, whereas fibrous cap thickness measured by log(VoA) had an absolute difference of 0.05 ± 0.09 mm compared to histology.

Figure 4 illustrates that, over all 14 examined plaques, median fibrous cap thickness measured by log(VoA) is more strongly correlated (R2 = 0.97) with the histological validation standard than that measured using PD (R2 = 0.79). Further, the CCC of 0.95 for log(VoA) versus 0.62 for PD suggests that ARFI log(VoA) enables more accurate and precise measurement of median fibrous cap thickness than ARFI PD. Figure 5 further supports that median fibrous cap thickness measurement is more accurate and precise by log(VoA) than by PD. While neither parameter’s bias was statistically significant (p<0.05), log(VoA) bias was 0.05 mm versus 0.10 mm for PD. Similarly, the reproducibility coefficient (RPC) and coefficient of variation (CV) were lower for log(VoA) (0.10 and 6.3%) than for PD (0.26 and 16%) median fibrous cap thickness measurements.

While the accuracy and precision of median fibrous cap thickness measurement suggest general utility, ability to measure minimum fibrous cap thickness indicates relevance to identify caps with high rupture potential. In figures 6 and 7, minimum fibrous cap thickness measures were more strongly correlated to the histological standard (R2 = 0.95 v. 0.74) and had lower error (SSE = 0.22 v. 0.05) when measured by log(VoA) versus PD. Moreover, log(VoA) measures of minimum fibrous cap thickness had lower RPC and CV (0.12 and 8.6%) than PD measures (0.27 and 20%). Interestingly, both log(VoA) and PD measures of minimum fibrous cap thickness had the same bias (0.11), but neither bias was statistically significant (p<0.05). These results show that log(VoA) enables more accurate and precise measures of minimum fibrous cap thickness than PD, suggesting that rupture potential is better determined by log(VoA).

Like median and minimum, log(VoA) outperforms PD in terms of accuracy and precision of maximum fibrous cap thickness measurement. Figure 8 shows that log(VoA) maximum fibrous cap thickness measures are more strongly correlated to the histological standard (R2 = 84 v. 0.67) and had lower error (SSE = 0.23 v. 0.35) than PD. Further, in fig. 9, log(VoA) had greater precision than PD (RPC = .29 v. .42; CV = 16% v. 21%). Finally, while both log(VoA) and PD measures of maximum fibrous cap thickness had statistically significant bias (p>0.05), the log(VoA) bias was −0.08 mm, while the PD bias was 0.08.

More accurate and precise median, minimum, and maximum fibrous cap thickness measurement by log(VoA) versus PD is consistent with results previously reported by Torres et al [28], which showed that contrast-to-noise ratio (CNR) for differentiating collagen from LRNC was 3.3 times greater by log(VoA) than by PD and that CNR for discriminating stiff from soft plaque features was 3.6 times greater. However, an unexpected outcome is that, for both log(VoA) and PD, maximum fibrous cap thickness measurement performance was worse than median and minimum cap thickness measurement performance. Specifically, maximum thickness measures were less correlated with the histological standard (PD R2 = 0.67 for maximum v. 0.79 for median and 0.74 for minimum, log(VoA) R2 = 0.84 for maximum v. 0.97 for median and 0.95 for minimum), had higher error (PD SSE = 0.35 for maximum v. 0.19 for median and 0.22 for minimum, log(VoA) SSE = 0.23 for maximum v. 0.03 for median and 0.05 for minimum), and had lower precision (PD RPC = 0.42 for maximum v. 0.26 for median and 0.27 for minimum, log(VoA) RPC = 0.29 for maximum v. 0.10 for median and 0.12 for minimum). The reasons for the observed poorer maximum fibrous cap thickness performance are yet to be determined.

It is interesting to consider that, relative to PD, log(VoA) yielded thinner fibrous cap delineations on both the lumen-cap (median difference of −0.33 ± 0.21 mm) and cap-LRNC (median difference of 0.21 ± 0.10 mm) interfaces. These data suggest that log(VoA) improves discrimination of fibrous cap from LRNC (which is consistent with results reported in [28]) and from luminal blood (which has not been previously shown). Future studies are needed to more comprehensively evaluate log(VoA)’s potential for discriminating plaque from blood under variable flow and clutter conditions.

Aspects of the study design may have influenced outcomes. First, fibrous cap thickness measurement performances by ARFI PD and log(VoA) were evaluated relative to histology-derived fibrous cap thickness, which was considered to be a validation standard. However, inconsistency between fibrous cap thickness in histology and ARFI images could arise due to plaque stretching and/or compression during in vivo imaging or due to sample shrinkage during histological processing. Plaque stretching and compression were minimized by acquiring in vivo data with gating to diastole, and specimens that were evidently warped were excluded from the study.

In addition, it is important to consider that the ARFI imaging focal depth could have impacted fibrous cap thickness measurement. In this study, the imaging focal depth was determined by the position of the carotid plaque and ranged from 1.8 to 2.3 cm across the examined plaques. Generally speaking, deeper focal depths experience lower radiation force magnitude [34, 35], and therefore smaller displacements, which could reduce fibrous cap contrast in PD and log(VoA) images. Further, tracking ARFI-induced displacements at deeper focal depths results in lower SNR and higher jitter, to the potential detriment of fibrous cap contrast by both PD and log(VoA). The impact of ARFI focal depth on fibrous cap thickness measurement is a topic of ongoing investigation.

Along with focal depth, the implemented tracking center frequency (6.15 MHz) and normalized axial cross-correlation displacement tracking kernel size (1.5λ) could have impacted fibrous cap thickness measurement. Czernuszewicz et al showed that for these values, the expected minimum fibrous cap thickness measurement resolution is 0.2 mm [26], which is comparable to the thickness of the thinnest fibrous cap included in this study. Notably, no caps thinner than 0.2 mm were contained in the available data set and, therefore, could not be evaluated. Using higher tracking center frequencies and/or smaller displacement tracking kernel sizes could improve thickness resolution, but at the potential cost of SNR and increases in jitter that impact fibrous cap contrast in PD and log(VoA) images. Comparing in vivo ARFI fibrous cap thickness measurement across tracking center frequencies and kernel sizes is work in progress.

Another factor impacting ARFI-based fibrous cap thickness measurement is reverberation clutter, which can be accentuated when calcium deposits are present in the plaque [25]. Clutter artifact corrupts displacement estimation as well as signal correlation and SNR and therefore diminishes fibrous cap contrast in PD and log(VoA) images. Advanced clutter filters and harmonic imaging could suppress clutter artifact and improve fibrous cap thickness measurement [36, 37].

Finally, while the results reported herein suggest that in vivo, human carotid fibrous cap thickness measurement is better supported by log(VoA) than by PD imaging, and while Bland Altman analyses and the CCC showed that performance improved when using log(VoA) in comparison to PD, the work is pilot in nature. After exclusions, only fourteen examples of fibrous caps with spatially matched histological validation were evaluated. Larger studies are needed in the future to more comprehensively compare ARFI PD and log(VoA) for fibrous cap thickness measurement.

V. Conclusions

This study demonstrates the potential of ARFI log(VoA) for improving fibrous cap thickness measurement in comparison to ARFI PD. In fourteen human carotid plaques, imaged in vivo, log(VoA)-derived fibrous cap thickness is more strongly correlated to true thickness, has a higher CCC, and is less variable than PD-derived fibrous cap thickness. Overall, these results add to the growing body of evidence that suggests that ARFI-based imaging, evaluating log(VoA) in particular, is relevant to delineating carotid plaque structure and composition for vulnerable carotid plaque detection.

Acknowledgment

The authors would like to thank Siemens Healthcare, Ultrasound Division, Issaquah, WA, USA, for technical support.

This work was supported in part by NIH grants R01HL092944, R01DK107740, R01NS074057, and T32HL069768.

Contributor Information

Gabriela Torres, Joint Department of Biomedical Engineering, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA, and North Carolina State University, Raleigh, NC 27695 USA..

Tomasz J. Czernuszewicz, Joint Department of Biomedical Engineering, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA, and North Carolina State University, Raleigh, NC 27695 USA. He is now with SonoVol, Inc., Durham, NC 27713 USA..

Jonathon W. Homeister, Department of Pathology and Laboratory Medicine, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA.

Mark A. Farber, Department of Surgery, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA.

Melissa C. Caughey, Joint Department of Biomedical Engineering, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA, and North Carolina State University, Raleigh, NC 27695 USA

Caterina M. Gallippi, Joint Department of Biomedical Engineering, University of North Carolina at Chapel Hill, Chapel Hill, NC 27514 USA, and North Carolina State University, Raleigh, NC 27695 USA..

References

  • [1].Mughal MM, Khan MK, DeMarco JK, Majid A, Shamoun F, and Abela GS, “Symptomatic and asymptomatic carotid artery plaque,” Expert Rev. Cardiovasc. Ther, vol. 9, no. 10, pp. 1315–30, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [2].Redgrave JNE, Lovett JK, Gallagher PJ, and Rothwell PM, “Histological assessment of 526 symptomatic carotid plaques in relation to the nature and timing of ischemic symptoms: the Oxford plaque study.,” Circulation, vol. 113, no. 19, pp. 2320–8, 2006. [DOI] [PubMed] [Google Scholar]
  • [3].Stary HC, “Natural history and histological classification of atherosclerotic lesions: an update,” Arterioscler. Thromb. Vasc. Biol, vol. 20, pp. 1177–8, 2000. [DOI] [PubMed] [Google Scholar]
  • [4].Shah PK, “Mechanisms of plaque vulnerability and rupture,” J. Am. Coll. Cardiol, vol. 41, pp. 15S–22S, February 2003. [DOI] [PubMed] [Google Scholar]
  • [5].Finn AV, Nakano M, Narula J, Kolodgie FD, and Virmani R, “Concept of vulnerable/unstable plaque,” Arterioscler. Thromb. Vasc. Biol, vol. 30, pp. 1282–92, 2010. [DOI] [PubMed] [Google Scholar]
  • [6].Moreno PR, “Vulnerable plaque: definition, diagnosis, and treatment,” Cardiol. Clin, vol. 28, pp. 1–30, 2010. [DOI] [PubMed] [Google Scholar]
  • [7].Saba L, Anzidei M, Sanfilippo R, Montisci R, Lucatelli P, Catalano C, Passariello R, and Mallarini G, “Imaging of the carotid artery.,” Atherosclerosis, vol. 220, no. 2, pp. 294–309, 2012. [DOI] [PubMed] [Google Scholar]
  • [8].Korshunov VA, Schwartz SM, and Berk BC, “Vascular remodeling - Hemodynamic and biochemical mechanisms underlying Glagov’s phenomenon,” Arterioscler. Thromb. Vasc. Biol, vol. 27, pp. 1722–1728, 2007. [DOI] [PubMed] [Google Scholar]
  • [9].Takaya N, Yuan C, Chu B, Saam T, Underhill H, Cai J, Tran N, Polissar NL, Isaac C, Ferguson MS, Garden GA, Cramer SC, Maravilla KR, Hashimoto B, and Hatsukami TS, “Association between carotid plaque characteristics and subsequent ischemic cerebrovascular events: a prospective assessment with MRI--initial results.,” Stroke, vol. 37, no. 3, pp. 818–23, 2006. [DOI] [PubMed] [Google Scholar]
  • [10].Dong L, Kerwin WS, Ferguson MS, Li R, Wang J, Chen H, Canton G, Hatsukami TS, and Yuan C, “Cardiovascular magnetic resonance in carotid atherosclerotic disease.,” J. Cardiovasc. Magn. Reson, vol. 11, no. 53, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [11].Watanabe Y, Nagayama M, Suga T, Yoshida K, Yamagata S, Okumura A, Amoh Y, Nakashita S, Van Cauteren M, and Dodo Y, “Characterization of atherosclerotic plaque of carotid arteries with histopathological correlation: vascular wall MR imaging vs. color Doppler ultrasonography (US).,” J. Magn. Reson. Imaging, vol. 28, no. 2, pp. 478–85, 2008. [DOI] [PubMed] [Google Scholar]
  • [12].Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Puliafito CA, et al. , “Optical coherence tomography,” Science, vol. 254, no. 5035, pp. 1178–1181, 1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Roleder T, Jąkała J, Kałuża GL, Partyka L, Proniewska K, Pociask E, Zasada W, Wojakowski W, Gąsior Z, and Dudek D, “The basics of intravascular optical coherence tomography,” Advances in Interventional Cardiology, 11(2), p.74–83, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [14].van de Poll SWE, Römer TJ, Puppels GJ, and van der Laarse A, “Imaging of atherosclerosis. Raman spectroscopy of atherosclerosis.,” J. Cardiovasc. Risk, vol. 9, no. 5, pp. 255–261, 2002. [DOI] [PubMed] [Google Scholar]
  • [15].Marcu L, Fang Q, Jo JA, Papaioannou T, Dorafshar A, Reil T, Qiao JH, Baker JD, Freischlag JA, and Fishbein MC, “In vivo detection of macrophages in a rabbit atherosclerotic model by time-resolved laser-induced fluorescence spectroscopy,” Atherosclerosis, vol. 181, no. 2, pp. 295–303, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [16].Nair A, Kuban BD, Tuzcu EM, Schoenhagen P, Nissen SE, and Vince DG, “Coronary plaque classification with intravascular ultrasound radiofrequency data analysis.,” Circulation, vol. 106, no. 17, pp. 2200–6, October 2002. [DOI] [PubMed] [Google Scholar]
  • [17].Wu X, Maehara A, Mintz GS, Kubo T, Xu K, Choi SY, He Y, Guo N, Moses JW, Leon MB, De Bruyne B, Serruys PW, and Stone GW, “Virtual Histology Intravascular Ultrasound Analysis of Non-Culprit Attenuated Plaques Detected by Grayscale Intravascular Ultrasound in Patients With Acute Coronary Syndromes,” Am. J. Cardiol, vol. 105, no. 1, pp. 48–53, 2010. [DOI] [PubMed] [Google Scholar]
  • [18].Roy-Cardinal MH, Destrempes F, Soulez G, and Cloutier G, “Assessment of carotid artery plaque components with machine learning classification using homodyned-K parametric maps and elastograms,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 66(3), pp.493–504, 2018. [DOI] [PubMed] [Google Scholar]
  • [19].Cloutier G, Cardinal MHR, Ju Y, Giroux MF, Lanthier S, and Soulez G, “Carotid plaque vulnerability assessment using ultrasound elastography and echogenicity analysis,” American Journal of Roentgenology, 211(4), pp.847–855, 2018. [DOI] [PubMed] [Google Scholar]
  • [20].Hansen HH, de Borst GJ, Bots ML, Moll FL, Pasterkamp G, and de Korte CL, “Compound ultrasound strain imaging for noninvasive detection of (fibro) atheromatous plaques: Histopathological validation in human carotid arteries,” JACC: Cardiovascular Imaging, 9(12), pp.1466–1467, 2016. [DOI] [PubMed] [Google Scholar]
  • [21].Schaar JA, de Korte CL, Mastik F, Strijder C, Pasterkamp G, Boersma E, Serruys PW, and van der Steen AF, “Characterizing vulnerable plaque features with intravascular elastography,” Circulation, 108(21), pp.2636–2641, 2003. [DOI] [PubMed] [Google Scholar]
  • [22].de Korte CL, van der Steen AF, Céspedes EI, Pasterkamp G, Carlier SG, Mastik F, Schoneveld AH, Serruys PW, and Bom N, “Characterization of plaque components and vulnerability with intravascular ultrasound elastography,” Physics in Medicine & Biology, 45(6), pp.1465–1475, 2000. [DOI] [PubMed] [Google Scholar]
  • [23].Nayak R, Korukonda S, and Doyley MM, “Strain estimation of carotid artery using virtual element based synthetic aperture imaging,” Medical Imaging: Ultrasonic Imaging, Tomography, and Therapy. Vol. 8675, p. 86750I, 2013. [Google Scholar]
  • [24].Korukonda S, Nayak R, Carson N, Schifitto G, Dogra V, and Doyley MM, “Noninvasive vascular elastography using plane-wave and sparse-array imaging,” IEEE transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 60(2), pp.332–342, 2013. [DOI] [PubMed] [Google Scholar]
  • [25].Czernuszewicz TJ, Homeister JW, Caughey MC, Wang Y, Zhu H, Huang BY, Lee ER, Zamora CA, Farber MA, Fulton JJ, Ford PF, and Gallippi CM, “Performance of acoustic radiation force impulse ultrasound imaging for carotid plaque characterization with histologic validation,” Journal of vascular surgery, 66(6), pp.1749–1757, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [26].Czernuszewicz TJ, and Gallippi CM, “On the feasibility of quantifying fibrous cap thickness with acoustic radiation force impulse (ARFI) ultrasound,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 63(9), pp.1262–1275, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [27].Geist RE, DuBois CH, Nichols TC, Caughey MC, Merricks EP, Raymer R, and Gallippi CM, “Experimental Validation of ARFI Surveillance of Subcutaneous Hemorrhage (ASSH) Using Calibrated Infusions in a Tissue-Mimicking Model and Dogs,” Ultrasonic imaging, 38(5), pp.346–358, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [28].Torres G, Czernuszewicz TJ, Homeister JW, Caughey MC, Huang BY, Lee ER, Zamora CA, Farber MA, Marston WA, Huang DY, and Nichols TC, “Delineation of Human Carotid Plaque Features in Vivo by Exploiting Displacement Variance,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 66(3), pp.481–492, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [29].Walker WF and Trahey GE, “A Fundamental Limit on Delay Estimation Using Partially Correlated Speckle Signals,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 42, pp. 301–308, 1995. [Google Scholar]
  • [30].Pinton GF, Dahl JJ, and Trahey GE, “Rapid tracking of small displacements with ultrasound,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 53, pp. 1103–1117, 2006. [DOI] [PubMed] [Google Scholar]
  • [31].Czernuszewicz TJ, Homeister JW, Caughey MC, Farber MA, Fulton JJ, Ford PF, and Gallippi CM, “Non-invasive in vivo characterization of human carotid plaques with acoustic radiation force impulse ultrasound: comparison with histology after endarterectomy,” Ultrasound Med Biol, vol. 41, pp.685–97, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [32].Lloyd S, “Least squares quantization in PCM,” IEEE Trans. Inf. Theory, vol. IT-28, no. 2, pp. 129–137, 1982. [Google Scholar]
  • [33].Lin L, and Torbeck LD, “Coefficient of accuracy and concordance correlation coefficient: new statistics for methods comparison,” PDA journal of pharmaceutical science and technology, 52(2), pp.55–59, 1998. [PubMed] [Google Scholar]
  • [34].Palmeri ML, McAleavey SA, Trahey GE, and Nightingale KR, “Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 53, pp.1300–1313, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [35].Czernuszewicz TJ, Streeter JE, Dayton PA, and Gallippi CM, “Experimental validation of displacement underestimation in ARFI ultrasound,” Ultrasonic imaging, 35(3), pp.196–213, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [36].Dahl JJ, Dumont DM, Allen JD, Miller EM, and Trahey GE, “Acoustic radiation force impulse imaging for noninvasive characterization of carotid artery atherosclerotic plaques: a feasibility study,” Ultrasound in Medicine & Biology, vol. 35, pp. 707–716, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [37].Trahey GE, Palmeri ML, Bentley RC, and Nightingale KR, “Acoustic radiation force impulse imaging of the mechanical properties of arteries: In vivo and ex vivo results,” Ultrasound in Medicine & Biology, vol. 30, pp. 1163–1171, 2004. [DOI] [PubMed] [Google Scholar]

RESOURCES