Abstract
Precise delineation of target tumor is a key factor to ensure the effectiveness of radiation therapy. While hybrid positron emission tomography-computed tomography (PET-CT) has become a standard imaging tool in the practice of radiation oncology, many existing automatic/semi-automatic methods still perform tumor segmentation on mono-modal images. In this paper, a co-clustering algorithm is proposed to concurrently segment 3D tumors in PET-CT images, considering that the two complementary imaging modalities can combine functional and anatomical information to improve segmentation performance. The theory of belief functions is adopted in the proposed method to model, fuse, and reason with uncertain and imprecise knowledge from noisy and blurry PET-CT images. To ensure reliable segmentation for each modality, the distance metric for the quantification of clustering distortions and spatial smoothness is iteratively adapted during the clustering procedure. On the other hand, to encourage consistent segmentation between different modalities, a specific context term is proposed in the clustering objective function. Moreover, during the iterative optimization process, clustering results for the two distinct modalities are further adjusted via a belief-functions-based information fusion strategy. The proposed method has been evaluated on a data set consisting of 21 paired PET-CT images for non-small cell lung cancer patients. The quantitative and qualitative evaluations show that our proposed method performs well compared with the state-of-the-art methods.
Index Terms—: Tumor co-segmentation, co-clustering, context information, information fusion, adaptive distance metric, spatial regularization, belief functions, PET-CT
I. Introduction
Precise segmentation of target tumor is indispensable in the practical process of radiation therapy. It assists in maximizing dose delivery in tumor tissues while minimizing side effects in organs at risk (OARs). Also, it is the basis for developing robust radiomic approaches for the prediction of therapy outcomes [1]–[3]. Positron emission tomography (PET), with the radio-tracer fluoro-2-deoxy-Dglucose (FDG), is a functional imaging modality that can non-invasively monitor metabolic activities of tumor cells. Target tumor usually demonstrates high standardized uptake values (SUVs) in FDG-PET images, which facilitates its differentiation from adjacent OARs (e.g. Fig. 1(a)). However, due to imprecise acquisition system and limited spatial resolution, positive tissues in PET images are blurry and noisy, which make it a challenging work for clinicians to precisely delineate tumors using solely PET images. Compared with PET, computed tomography (CT) is poor in contrast for the discrimination between tumor tissues and OARs, but it have relatively high spatial resolution, and can provide detailed anatomical information as well (e.g. Fig. 1(b)). In addition, the calculation of radiation dose depends on knowledge from CT images. The development of hybrid PET-CT scanner effectively combines the complementary information from the two distinct imaging modalities. While PET-CT has become a standard imaging technique in radiation oncology, many existing automatic/semi-automatic methods still delineate tumor volumes in mono-modal images.
Fig. 1.
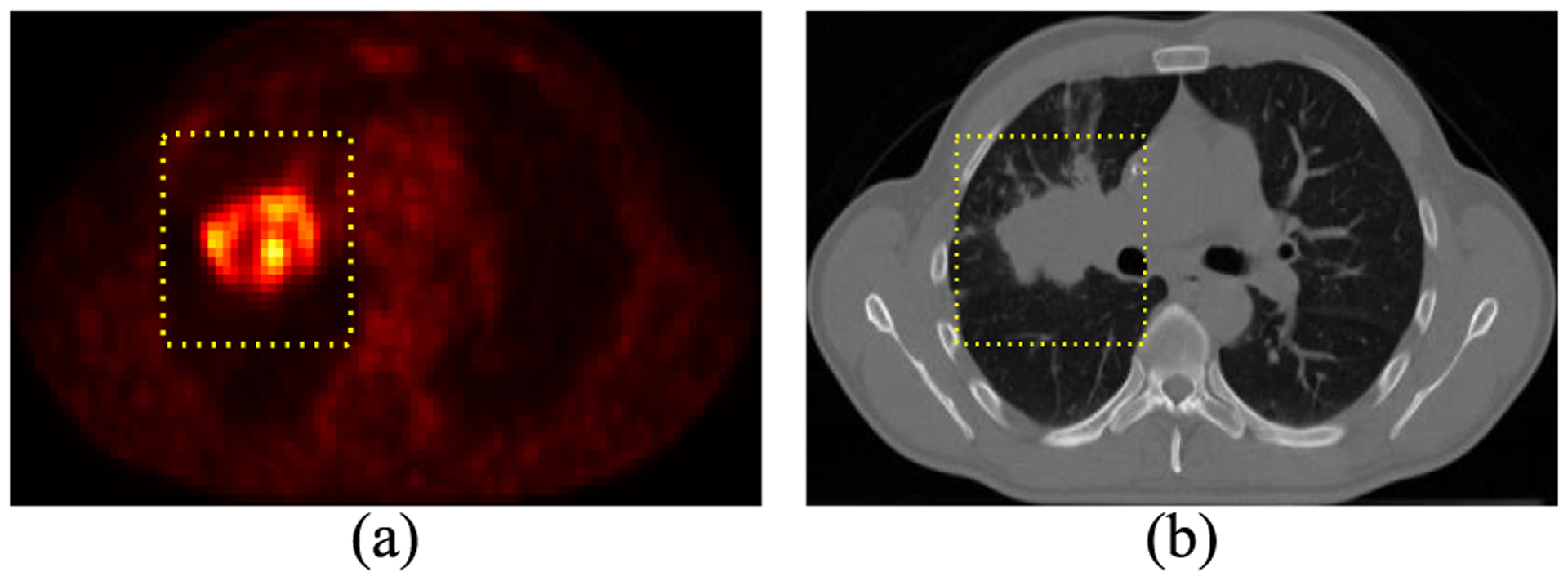
A tumor shown in integrated PET-CT images: (a) FDG-PET image in the axial plane and (b) the corresponding CT. The yellow dotted box indicates the volume of interest (VOI).
Diverse mono-modal methods for automatic/semi-automatic segmentation of target tumor in PET images have been proposed [4], [5], which include thresholding methods [6], [7], region growing methods [8], [9], methods based on level set/active contours [10], [11], graph-based methods [12]–[14], gradient-based methods [15], [16], statistical methods [17]–[19], supervised learning methods [20], [21], and clustering methods [22]–[26]. Deep convolutional neural networks (CNN) [27] have also been applied to segmenting PET tumors [28]. It is worth noting that clustering methods have shown competitive performance in tumor delineation, especially considering that tumor tissues of different patients usually present heterogenous uptakes and irregular contours [4]. For example, an improved FCM (i.e., FCM-SW) method was proposed in [23] for the segmentation of heterogeneous PET tumors. A generalized FCM (i.e., SPEQTACLE) method was proposed in [25], where the fuzzy distributions of PET images were taken into account during tumor delineation. A spatial evidential clustering (i.e., SECM) method was proposed in [24] for the segmentation of lung tumors in multi-tracer PET images. More recently, a novel evidential clustering method (i.e., ECM-MS) was proposed in our previous study [26] to delineate target tumor using solely PET images, where the most informative imaging features were automatically selected to reliably quantify clustering distortions and spatial smoothness.
Some other methods use information from one modality to guide the delineation of target tumor in another modality [29]–[31]. For example, Mu et al. [31] proposed an improved level set method to segment tumor in FDG-PET images, where knowledge from corresponding CT images was adopted to guide the initialization of zero level set. In [30], Wojak et al. proposed a joint variational segmentation method, in which PET information is regarded as a local constraint to adjust the segmentation results in CT images. These methods attempted to delineate a unique contour in PET and CT images, without considering that the two distinct imaging modalities actually demonstrate complementary while distinct characteristics of the same target.
Up to now, most existing methods for tumor cosegmentation in PET-CT images are graph-based [32]–[37]. In [34], by constructing a hyper graph, a random walk method was proposed for automatic co-segmentation of multimodal medical images (e.g. PET-CT and PET-MRI). In [33], an extension of [32], the co-segmentation was formulated as a binary labeling problem of Markov random field (MRF) on a graph consisting of two sub-graphs. The two sub-graphs correspond to PET and CT images, respectively; the interaction between them was modeled by an adaptive context energy. A maximum flow graph cut algorithm was then adopted to solve the formulated MRF optimization problem for consistent co-segmentation. In [36], the random walk and graph cut methods were effectively combined, where the random walk was performed on PET images as a stable initialization to improve the co-segmentation performance of the subsequent maximum flow graph cut with a specific energy function. In [37], a topology graph was combined with an intensity graph to improve graph cut with topology modeling for semiautomatic segmentation of target tumor in PET-CT images. Although these graph-based methods are efficient and intuitive for the co-segmentation task, their performance may be influenced by the quality of predefined tumor and background seeds. In addition, they make decision only according to the information provided by intensity values of image voxels, while other imaging features, e.g., texture features [38]–[40], describing the spatial context of each voxel are ignored.
Apart from these graph-based approaches, some other methodologies, e.g., active contours [41], supervised learning [42], [43], and stochastic modeling [44], [45], have also been applied to co-segmenting multi-modal medical images. For example, in [42] and [43], textural features were extracted from PET-CT images to train classification models for the identification of tumor voxels. A statistical method based on hidden Markov tree (HMT) was proposed in [44] for tumor co-segmentation in PET-CT images preprocessed by wavelet/contourlet enhancement. A hidden Markov fields (HMF) based method was proposed in [45] for joint tumor segmentation in multi-modal medical images, where a copula-based fusion strategy was adopted to model dependency between different modalities. One critical challenge for the application of such statistical methods on PET-CT co-segmentation is how to conjointly define stochastic distributions of PET and CT voxels that could be very different. CNN-based approaches have also shown promising performance for multi-source medical image segmentation. For example, a multi-scale CNN method was proposed in [46] to segment tumor in multi-modal MRI. More recently, a multi-channel multi-scale encoder-decoder network (i.e., M2EDN) method was proposed in [47] to learn task-oriented fusion of multi-source information for brain structure segmentation in MRI. These deep learning methods are also applicable in PET-CT tumor co-segmentation, while limited number of training samples (i.e., PET-CT images) may potentially hamper the segmentation performance. Also, similar to [29]–[31], the above active contour-based, statistical, and learning-based co-segmentation methods [41]–[47] tend to yield a unique contour in both PET and CT images, ignoring the specificity of each modality.
Effectively modeling uncertainty and imprecision inherent in PET and PET-CT images is of great concern for accurate segmentation of blurry and inhomogeneous targets [19]. In our study, this critical issue is addressed via the theory of belief functions (BFT) [48]. As a powerful tool for representing and reasoning with partial (imprecise, uncertain) knowledge, BFT can provide reliable ways to fuse information from different sources, turning out to be effective for joint tumor delineation in PET-CT images. Based on BFT, we propose a co-clustering method to concurrently segment volumetric PET and CT images in a unified framework. Diverse imaging features are extracted for the comprehensive characterization of PET and CT voxels, while without prior knowledge concerning the most informative ones. As an extension of our previous mono-modal method [26], a joint feature selection and distance metric adaptation procedure is included in the proposed co-clustering method to ensure reliable quantification of clustering distortions for both PET and CT images. In addition, a specific spatial regularization is also included to protect local homogeneity in each mono-modality. To encourage consistency between PET and CT, a special context term is proposed to softly penalize conflicting segmentation in the two distinct but also complementary modalities. During the iterative process of clustering, results in PET and CT are further adjusted by fusing them via the Dempster’s combination rule [48], considering that knowledge from one modality could be regarded as additional evidence to assist the segmentation in the other one.
The rest of this paper is organized as follows. BFT is briefly recalled in Section II. The proposed co-segmentation method is then introduced in Section III. In Section IV, the proposed method is evaluated by a cohort of real-patient PET-CT images. Some discussions and the conclusion are presented in Section V and Section VI, respectively.
II. Theory of Belief Functions
The theory of belief functions (BFT) is also known as the Dempster-Shafer theory or evidence theory [48]. It has been successfully applied in diverse fields, including image analysis [49]–[52], and data classification/clustering [53]–[59], etc. As a formal framework for modeling, fusing, and reasoning with partial (uncertain, imprecise) information, BFT extends both the set-membership approaches and probability theory, and has strong connections with other theories of uncertainty, e.g., possibility theory and imprecise probability. BFT has two main components, i.e., the quantification of pieces of evidence, and the combination of quantified evidence.
A. Evidence Quantification
In the framework of belief functions, we reason under uncertainty based on the modeling of evidence [48]. Let ω be a variable taking values in a finite domain Ω = {ω1,·…, ωc}, called the frame of discernment. An item of uncertain evidence regarding the actual value of ω can be represented by a mass function m on Ω, defined from the powerset 2Ω to the interval [0, 1], such that
| (1) |
Each mass m(A) denotes a degree of support attached to the proposition “the true value of ω is in the subset A”, and to no more specific proposition. Function m is said to be normalized if m(∅) = 0, where the empty set denotes hypothesis beyond the finite domain Ω. Any subset A with m(A) > 0 is called a focal element. In particular, if all focal elements of a mass function are singletons, it is said to be Bayesian, and is then equivalent to a probability distribution. A mass function with only one focal element is said to be categorical, and is then equivalent to a set.
We can associate belief and plausibility functions to a normalized mass function m, from 2Ω to [0, 1], which are defined as:
| (2) |
for all A ⊆ Ω. Quantity Bel(A) can be interpreted as the degree to which the evidence supports A (also known as credibility), while Pl(A) can be interpreted as the degree to which the evidence is not contradictory to A. Functions Bel and Pl are in one-to-one correspondence with mass function m. For all A ⊆ Ω, we always have Bel(A) ≤ Pl(A), which indicates that the belief (or probability) supporting the proposition “ω ∈ A” is bounded by the corresponding credibility and plausibility.
B. Evidence Combination
A key operation in BFT is that beliefs are elaborated by fusing evidence from multiple information sources. The basic mechanism for evidence combination is Dempster’s rule [48]. Let m1 and m2 be two mass functions derived from independent items of evidence. They can be fused using Dempster’s rule to form a new mass function m1⊕2 defined as
| (3) |
for all A ⊆ Ω \ ∅, where . It is worth noting that Dempster’s rule generalizes set intersection and probabilistic conditioning, by which beliefs can be refined after information fusion.
For example, let m1 and m2 be two independent mass functions to help reasoning the actual value of an object. They are defined on a frame of discernment Ω = {ω1, ω2}, which means that all possible values of the studied object are included in Ω. Thus, large value of m1(Ω) or m2(Ω) reflects that the corresponding piece of evidence is imprecise, since m1(Ω) and m2(Ω) quantify the degree of support attached to the hypothesis “the actual value of the studied object is in Ω”, which does not provide any more specific indications. Assuming m1 and m2, and their combination via (3), i.e., m1⊕2, have the form of
| A | m1(A) | m2(A) | m1⊕2(A) |
|---|---|---|---|
| {ω1} | 0.5 | 0.2 | 0.56 |
| {ω2} | 0 | 0.2 | 0.11 |
| Ω | 0.5 | 0.6 | 0.33 |
According to m1(Ω) = 0.5 and m2(Ω) = 0.6, we can observe that both m1 and m2 are severly imprecise, while the fusion of them effectively reduces the imprecision to m1⊕2(Ω) = 0.33. In addition, we can also find that the mass function m1⊕2 after information fusion also reduces the uncertainty in both m1 and m2, as the belief associated with the proposition “the actual value of the object is ω1” has increased to 56%, i.e., m1⊕2({ω1}) = 0.56.
However, to ensure the effectiveness of Dempster’s combination rule, mass functions from distinct information sources should not contain high conflicts (which means large Q in (3)). To quantify the conflicts or inconsistence between different bodies of evidence, abounding dissimilarity measurements have been proposed, in which the metric dJ designed by Jousselme et al. [60] is a commonly used one. For any two mass functions m1 and m2, their dissimilarity dJ(m1, m2) is quantified as
| (4) |
where J is a positive definite matrix whose elements are Jaccard indexes, i.e., J(A, B) = |A ∩ B|/|A ∪ B|, ∀A, B ∈ 2Ω\∅. The quantification (4) satisfies the requirements for a valid distance metric. In addition, it effectively accounts for the interaction between the focal elements of Ω [60], thus can truthfully reflect the conflicts between different pieces of evidence.
For instance, assume that m1, m2, and m3 are three mass functions on Ω = {ω1, ω2}, with the form of
| A | m1(A) | m2(A) | m3(A) |
|---|---|---|---|
| {ω1} | 0.7 | 0.2 | 0.2 |
| {ω2} | 0 | 0 | 0.5 |
| Ω | 0.3 | 0.8 | 0.3 |
We can observe that m1 is in consistence with m2, as m1({ω2}) = m2({ω2}) = 0; while, on the other hand, both m1 and m2 contradicts with m3, since the latter piece of evidence concentrated on ω2 with m3({ω2}) = 0.5. If we use directly the Euclidean metric to quantify the dissimilarity between these three mass functions, ||m1 − m2||2 = ||m1 − m3||2 = 0.71 is inappropriate, because it does not reflect the actual situation. However, if (4) is applied with
| (5) |
to calculate the dissimilarity, the results are dJ(m1, m2) = 0.35 and dJ(m1, m3) = 0.50, which effectively reflect that m1 is more consistent with m2 than with m3.
III. Method
First of all, image features are extracted from a 3-D region of interest (ROI) in each mono-modality. The ROI is a cuboid defined by users, which fully includes the target tumor, such as the yellow dotted box shown in Fig. 1. Let be feature vectors in for n voxels in PET, while for the corresponding n voxels in CT. Using these extracted features, the proposed method co-segments tumor in the two distinct modalities via concurrently looking for matrices and , where are, respectively, the mass functions for voxel i in PET and CT. For PET (resp. CT), (resp. ) quantifies the mass of belief attached to all possible propositions with respect to its cluster. We assume that all the voxels belong either to the background (i.e. hypothesis ω1) or to the positive tissue (i.e. hypothesis ω2), without existence of outliers. Thus, the whole frame of clusters is set as Ω = {ω1, ω2}. The mass function for each voxel, both in PET and CT, obeys mi({ω1}) + mi ({ω2}) + mi(Ω) ≡ 1. As mi(Ω) measures the ambiguity regarding the clusters ω1 and ω2, blurring boundary and severe heterogeneous regions will have large mass on Ω. Finally, the crisp segmentation is obtained by making decisions based on Mpt and Mct.
As a co-clustering algorithm, the proposed method searches for a pair of Mpt and Mct via minimizing a global cost function, which is constructed by independent costs in each modality, and context cost deduced by inconsistent segmentation between the two distinct but complementary modalities.
A. Cost for Segmentation in Mono-Modality
The cost for each mono-modality is an extension of a classical evidential clustering algorithm [53], with a form similar to that in our previous mono-modal method [26]. The novelty is that a specific spatial regularization and distance metric adaptation procedure are integrated for clustering image voxels. Without loss of generality, the following discussion taking the cost for PET, i.e., , as an example:
Let cluster ω1 (resp. ω2) be represented by a center (resp. ) in . For each nonempty subset Aj ⊆ Ω \ ∅, we assume that its prototype is defined as the barycenter of the centers associated to the singletons composing Aj, i.e.,
| (6) |
where skj is binary, and it equals 1 if and only if ωk ∈ Aj; while cj = |Aj| denotes the cardinality of Aj. To learn Mpt in an unsupervised way, is then defined as
| (7) |
which consists of four terms:
1). Term 1:
Similar to the original ECM, the first term of (7) denotes the restriction between clustering distortions and mass functions.
2). Term 2:
The second term of (7) is a spatial regularization defined in the framework of belief functions for enhancing local homogeneity of neighboring voxels. According to the spatial prior of a PET volume, matrix that we want to learn can be regarded as a specific random field, matrix where each mass function is a random vector in , and its distribution depends on the mass functions of adjacent voxels. Let be a 3-D neighborhood system, where Φ(i) = {1, …, T} is the set of the T neighbors for voxel i. The corresponding mass functions of voxels in Φ(i) are , while the feature vectors of these voxels are . Then, based on the above assumption about Mpt, of (7) quantifies the smoothness around voxel i, where denotes the distance between voxel i and its neighbor t in the feature space; while, measures the independence between and , i.e., the inconsistency between the mass functions of voxel i and its neighbor t. Based on (4), we set , where matrix J is defined by (5).
3). Term 3:
To describe image voxels, we include textural features as complementary information for voxel intensities. The challenge to this end is that a large amount of textural features can be extracted, but without prior knowledge concerning the most informative features. In addition, the quantified high-dimensional feature vectors may contain unreliable variables due to noise and limited resolution of PET images. To tackle this challenge, distance metric adaptation and/or feature selection (e.g., [61]) are desirable.
In our previous work [62], a supervised method has been proposed to learn a low-rank dissimilarity metric for improving the performance of distance-based classifiers on high-dimensional datasets containing unreliable and imprecise features. Distinct from this previous work, here our goal is to adapt distance metric for given data in an unsupervised learning protocol, so as to improve the performance of clustering algorithms. Therefore, we look for a matrix during clustering, under the constraint q ≪ p, by which the dissimilarity between any two feature vectors, say and , can be quantified as
| (8) |
A desired matrix Dpt transforms the original feature space to a low-dimensional subspace, where discriminant input features play a more significant role than uninformative ones in calculating the dissimilarity. To find such a Dpt, the distortion between any and cluster centroid , i.e., in the first term of (7), is represented by (8). Moreover, the spatial regularization is also used to adapt the distance metric, where is also quantified by (8). During the iterative minimization of (7), a large dissimilarity between and will indicate that Dpt obtained as current step is unfit. Then, it should be adjusted at the next step to reduce the dissimilarity between and , so as to bring adjacent voxels closer.
To ensure the effectiveness of metric updating, the third term of (7) is defined as the sparsity regularization ||Dpt||2,1 of matrix Dpt, i.e., . It aims at selecting the most reliable input features to calculate distance d2(·, ·) in the feature space (which exists in the other three terms). By forcing rows of Dpt to be zero, the proposed method only selects reliable features for clustering, while the influence of unreliable features is controlled. Scalar λ is a tuning parameter that controls the influence of this regularization.
4). Term 4:
The last term of (7) is used to prevent the cost function being trivially solved with Dpt = 0, which collapses all the features vectors into a single point. Vectors and are two seeds for the positive tissue and the background, respectively, which can be predetermined automatically. We empirically set a constant parameter (i.e., = 1) for this term, mainly considering it serves to prevent Dpt = 0, in which case the penalty will be activated and the corresponding loss will get close to infinity. In addition, we experimentally found that this term is insensitive to changing parameters.
B. Cost for Inconsistency Between PET and CT
The proposed method encourages consistent segmentations for PET and CT images, while not force them to be identical, as the information provided by the two distinct modalities may be partially contradicts with each other. These partial conflicts are possibly caused by multiple reasons, e.g., the lowcontrast property of CT, the blurring nature of PET, and the impropriate correspondence between PET and CT voxels that are brought by the uncertainties in registration of these two distinct modalities.
According to the above assumption, the disagreement between PET and CT segmentations can be softly modeled by the dissimilarity between and . Thus, based on the metric introduced in (4), the context penalty i.e., , is defined as
| (9) |
where and are the mass functions of two corresponding voxels in PET and CT images, respectively; while, J is the matrix introduced in (5).
To sum up, according to the discussions in Section III-A and Section III-B, the proposed co-clustering method looks for a pair of and via minimizing a global cost function:
| (10) |
subject to the constraints , , and
| (11) |
for all i = 1, …, n, and Aj ⊆ Ω \ ∅. In (10), and denote, respectively, the cost in PET and CT that quantified by (7); while, is the context term (9) to quantify the inconsistence between segmentation in PET and CT; parameter γ controls the influence of this inconsistence.
C. Iterative Minimization of the Cost
To find the best pair of Mpt and Mct, we propose to minimize the global cost function (10) in an iterative scheme. The optimization procedure is summarized in Algorithm 1, which can be detailed as follows.
1). Initialization:
We initialize the mass functions (i.e. Mpt and Mct) and the singleton cluster centers (i.e. Vpt and Vct) for both PET and CT via the original ECM algorithm. Based on the initial mass functions that obtained in PET, a very limited number of tumor and background seeds are predefined. After that, the two feature vectors, i.e., (resp. ) and (resp. ), used in the last term of (7) are calculated as the barycenters of the tumor and background seeds, respectively. The output dimension, namely the number of columns in feature transformation matrix Dpt (resp. Dct), is then determined by applying principle component analysis on all the feature vectors (resp. ). The initial Dpt (resp. Dct) is constructed by the top 95% eigenvectors.
The optimization procedure alternates between three parts: the clustering in PET, the clustering in CT, and the fusion of Mpt and Mct at current step. For the clustering in each monomodality, the optimization iterates between cluster assignment (i.e. Mpt or Mct estimation) in the E-step, and both prototype determination (i.e. Vpt or Vct estimation) and distance metric adaptation (i.e. Dpt or Dct estimation) in the M-step.
2). Optimization in PET:
This procedure only relates to the minimization of the first term and the last term of (10), which is performed in an EM-like protocol.

a). E-Step:
Given Vpt, Dpt, and Mct, the minimization of (10) turns to be a quadratic problem with respect to . The derivative of (10) concerning the mass function , ∀i = 1, …, n, can be written as
| (12) |
where the matrix J is defined by (5), is measured by (8), is the mass function for the corresponding ith voxel in CT, and
| (13) |
where is determined by (6), ∀Aj ∈ {{ω1}, {ω2}, Ω}, and is calculated by (8). Based on the derivation (12), and using Mpt and Mct obtained by the last step as initializations, an efficient interior-point algorithm with a limited-memory BFGS approximation of the Hessian matrix [63] is adopted to solve the quadratic problem, so as to obtain a desired matrix Mpt at current step.
b). M-Step I:
Updating matrix Vpt of clustering centers is only influenced by the first term of (10). Let and , ∀Aj ∈ {{ω1}, {ω2}, Ω}. According to (6), the centers of clusters ω1 and ω2 are calculated, respectively and directly, as
| (14) |
c). M-Step II:
Similar to M-step I, the optimization of Dpt relates to the first term of (10), i.e., quantified by (7). The objective function (7) is only partly differentiable as a function of Dpt, where the sparsity regularization ||Dpt||2,1 has a singularity at Dpt = 0. The derivative of the differentiable part of (7) concerning Dpt can be written as
| (15) |
based on which the Beck-Teboulle proximal gradient algorithm [64] is adopted to search for a qualified Dpt at current step, using Dpt obtained at the last iteration as the initialization.
3). Optimization in CT:
The adaptation of Mct, Vct, and Dct, which relates to the last two terms of (10), is following the same way as that for Mpt, Vpt, and Dpt discussed above. To update Mct at current step, Mpt obtained by Section III-C2 is utilized in (12).
4). Fusion of PET and CT:
It is worth noting that Mpt and Mct obtained in Section III-C2 and III-C3 are in fact two independent pieces of evidence regarding the same target tumor. They are complementary, as PET and CT can provide, respectively, functional and anatomical information. In addition, they are also consistent due to the soft context term defined by (9). Therefore, in this step, Mpt is further updated by fusing it with Mct via the Dempster’s rule (i.e. (3)). The updated Mpt is then used as the initialization for the optimization (i.e. Section III-C2) in the next iteration.
The whole optimization procedure will not terminate the alternation between the steps described in Section III-C2, III-C3, and III-C4, until the value of (10) has no significant change between two consecutive iterations.
D. Decision Making
Mass functions obtained by Algorithm 1 can be further refined. Without loss of generality, for an arbitrary voxel i, we assume that {mi, 1, …, mi, T} are mass functions obtained by the clustering algorithm that correspond to voxels in its neighborhood Φ(i), i.e., adjacent voxels surrounding i. These mass functions can be regarded as T independent pieces of evidence to help reasoning the actual cluster of i. The reliability of evidence mi,t to voxel i, ∀t ∈ {1, …, T}, is inversely proportional to the spatial distance between voxel i and t. Let this spatial distance be , and based on Dempster’s discounting procedure [48], mi,t can be weighted by a coefficient to obtain a discounted mass function:
| (16) |
Then, using the Dempster’s rule of combination (3), all the T discounted mass functions are fused with the mass function mi to output a renewed mass function mi. This procedure is applied to both PET and CT. It can also be regarded as a BFT-based filtering operation in a small cubic window.
Finally, based on refined mass functions, crisp clustering of PET and CT voxels is performed via maximizing the plausibility values calculated by (2).
IV. Materials and Experiments
In this section, our proposed co-clustering algorithm was evaluated on 21 volumetric FDG-PET/CT images acquired for non-small cell lung cancer (NSCLC) patients. First, our proposed co-clustering method was compared with its mono-modal variant (i.e., ECM-MS [26]). Then, it was further compared with other sate-of-the-art segmentation methods, including four mono-modal methods, i.e., 3D-LARW [12], FCM-SW [23], SECM [24], and ECM [53], and two co-segmentation methods, i.e., HMT [44] and M2EDN [47].
A. Material and Features
Totally 21 FDG-PET-CT images of NSCLC patients were studied, which were acquired on a Biograph LSO Sensation 16 (Siemens Medical Solutions, Hoffman Estates, Knoxville, TN, USA). The PET images were smoothed with a Gaussian filter (full width at half maximum = 5 mm) after reconstruction. They had the same anisotropic resolution of 4.06 × 4.06 × 2 mm3, and the size of the axial PET slices was 168 × 168. The spatial resolution of the corresponding CT images was 0.98 × 0.98 × 3 mm3, and the size of the axial CT slices was 512 × 512. The tumor lesions were manually delineated by experienced clinicians in PET by the guidance of the corresponding CT. These tumor lesions were mostly located in or near the mediastinum, and some of them were located in the apex, without significant respiratory displacements at visual inspection of the gated images. Generally, these tumor lesions demonstrated heterogenous FDG uptake, and had various sizes ranging from 1.9 mL to 135.8 mL.
Considering that the image resolution is anisotropic, in our experiments, a 3 × 3 window in 2-D was defined to extract features both in PET and CT images; moreover, for simplicity, the same kinds of features were extracted in both of them. Using the predefined box, the average intensity value, the maximum intensity, the minimum intensity, the range of intensity value (i.e., maximum–minimum), and the standard deviation of intenstiy were calculated as features for the centering voxel. The gray level size zone matrix (GLSZM) [40] was adopted to extract seven texture features, as its effectiveness in medical image characterization has already been evaluated [1]. Similarly, the gray-level co-occurrence matrix (GLCM) [38] was also utilized to extract fifteen features. To sum up, for each PET and CT voxel, a 28-dimensional feature vector was extracted, consisting of 6 intensity-based, 7 GLSZM-based, and 15 GLCM-based features.
In consideration of computational costs, after extracting features in PET and CT independently, data in CT were downsampled to PET. Each voxel (and its feature vector) in CT corresponds to one voxel in PET.
B. Evaluation Criteria
The manual delineation by experienced clinicians was performed on PET images by the guidance of the corresponding CT images. Regarding the manual delineation as the reference, all the segmentation methods were comprehensively evaluated by five criteria, including Dice coefficient (DSC), sensitivity (SEN), positive predictive value (PPV), Hausdorff distance (HD), and mean absolute surface distance (MSD). Let TP, FP, TN, and FN denote the true positive, false positive, true negative, and false negative segmentation, respectively. We define DSC = 2TP/(2TP + FP + FN), SEN = TP/(TP + FN), and PPV = TP/(TP + FP). The HD metric quantifies the maximum distance between the boundary points of two different segmentations. Complementarily, the MSD metric measures the average difference between two segmentation surfaces.
C. Parameter Setting
The three tuning parameters utilized in the proposed method, i.e., η, λ, and γ, control, respectively, the influence of the spatial regularization, the influence of the sparsity regularization, and the consistence of the segmentation in PET and CT. In our experiments, λ and γ were empirically set to 8 and 0.001, respectively; while, to maximize the segmentation performance, the influence of the spatial penalty should be determined by taking into account the size of tumors. More specifically, η was empirically set to 0.003 and 0.2 for large and small tumors, respectively. To this end, we first roughly pre-estimated the size of the to-be-segmented tumor based on the initialization by the original ECM. Then, we empirically regarded tumors with the rough volume less than 40 mL as relatively small ones. The influence of these parameters will be further analyzed in the discussion part (i.e. Section V).
D. Results
1). Illustrative Results of Co-Segmentation:
An example to illustrate the co-segmentation performance of the proposed method is shown in Fig. 2, where each row represents a different slice in the axial plane of the same tumor. In the first and second column, contours delineated in PET (green) and CT (magenta), are compared respectively to the ground truth (blue); while, in the last column, all of them are overlaid in the fused images. As can be seen, segmentation in PET is in consistent with that in CT, while they are not identical. The 3-D tumor volumes in PET and CT are further shown in Fig. 3, where the green, magenta, and orange regions represent, respectively, true positive voxels, false positive voxels, and false negative voxels, as compared to the ground truth.
Fig. 2.
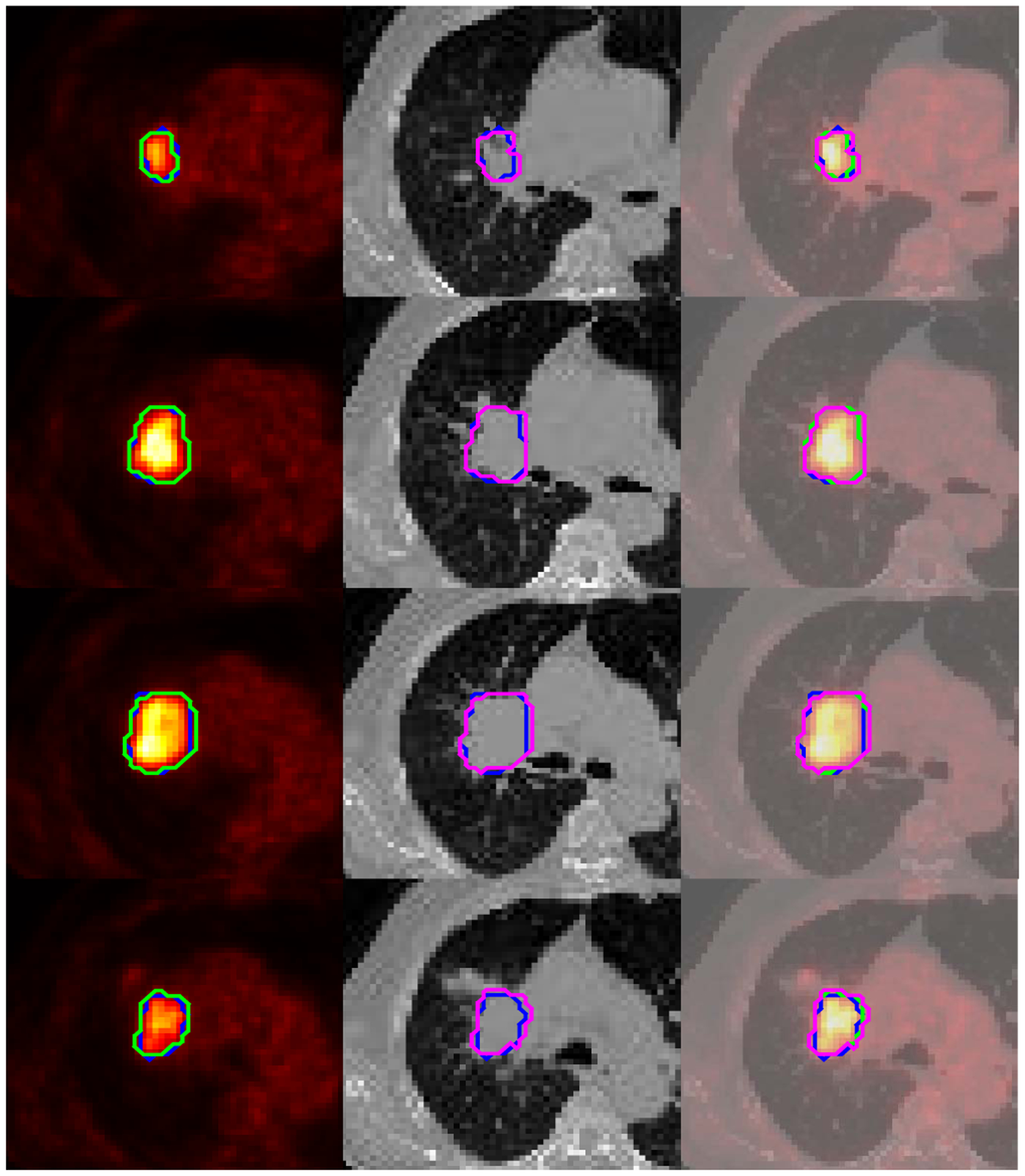
A co-segmentation example shown in the axial plane, where contours delineated in PET (green) and CT (magenta) are compared to the ground truth (blue) in the first and the second column, respectively; in the last column, all the contours are overlaid in the fused images.
Fig. 3.
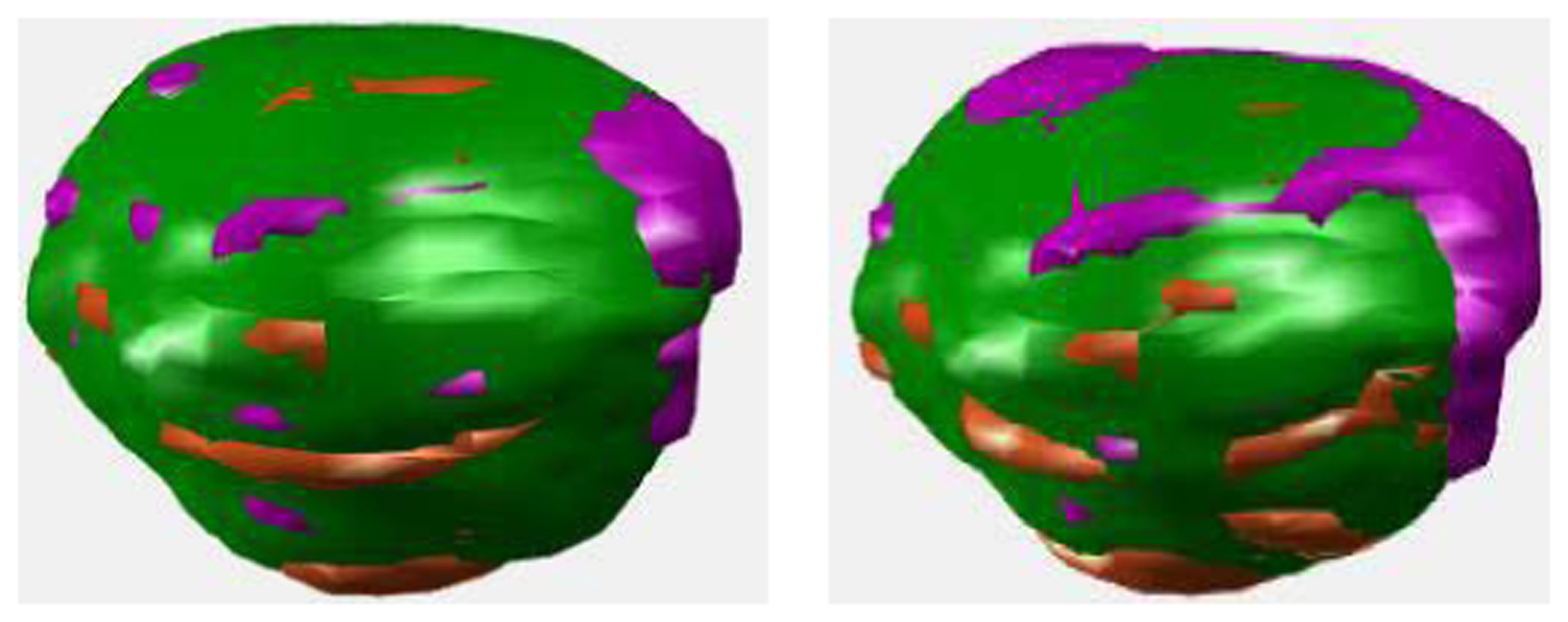
Tumor volumes segmentated in PET (first column) and CT (second column), where, as compared to the ground truth, where, the green region consists of the true positive and true negative voxels, the magenta region consists of the false positive voxels, while the orange region consists of the false negative voxels.
2). Co-Segmentation vs. Mono-Modal Segmentation:
To demonstrate the effectiveness of the proposed co-segmentation method, its performance was compared with that of monomodal segmentation in PET and CT. In our experiments, mono-modal segmentation was performed by ECM-MS [26], i.e., by setting γ in (10) to zero, and removing simultaneously the fusion procedure described in Section III-C4.
Two illustrative results are shown in Fig. 4, from which we can find that co-segmentation outperformed independent segmentation in PET and CT in both two cases. Correspondingly, the quantitative results on the 21 subjects are summarized in Table I, from which we can find that co-segmentation led to the best performance in terms of all the five metrics, compared to independent segmentation produced by our previous mono-modal method (i.e., ECM-MS [26]). More specifically, it is worth noting that our previous ECM-MS obtained good segmentation performance in segmenting PET images, which thanks to two main reasons: 1) PET images are high in contrast; 2) blur and heterogeneity inherent in them were effectively handled in the framework of belief functions, with the help of the proposed spatial regularization and distance metric adaptation procedure. The extension of ECM-MS, i.e., the proposed co-clustering algorithm, further improved the segmentation in PET images, as anatomical information from CT images was included as the complementary knowledge for more accurate tumor delineation. On the other hand, the segmentation in CT images was greatly improved by the co-segmentation strategy. It is mainly because the boundary between target and background is invisible in CT images, which was effectively tackled by co-segmentation via incorporating functional information from PET images.
Fig. 4.
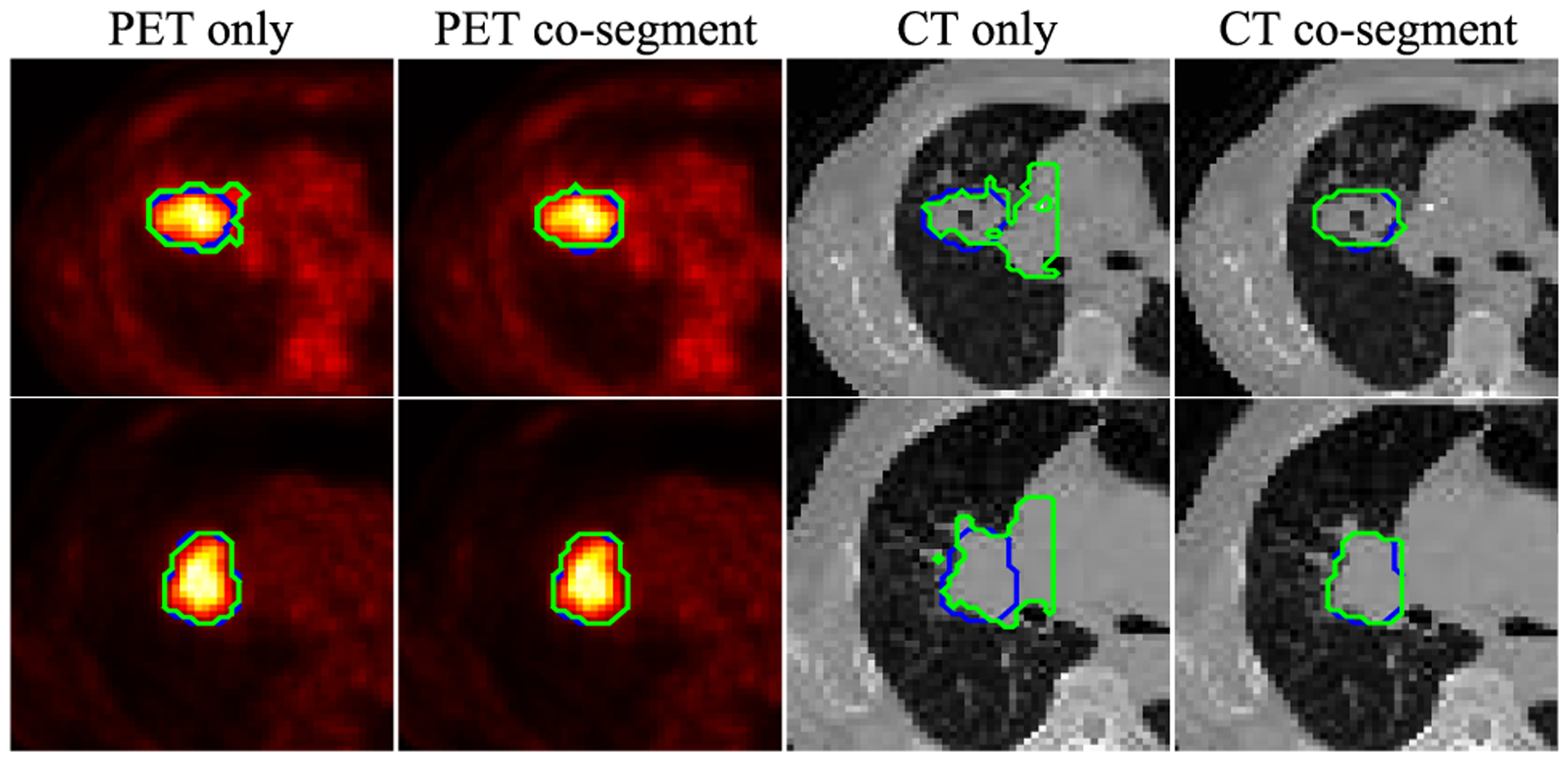
Comparing mono-modal segmentation to co-segmentation in PET. The two rows correspond to two different examples. The green and blue contours denote, respectively, the automatic segmentation and the reference.
TABLE I.
Quantitative Segmentation Results (Mean ± Standard Deviation) Obtained by the Proposed Method Based on Co-Segmentation and Mono-Modal Segmentation, Respectively
| PET only | Co-segment PET | CT only | Co-segment CT | |
|---|---|---|---|---|
| DSC | 0.86 ± 0.05 | 0.87 ± 0.04 | 0.29 ± 0.17 | 0.86 ± 0.04 |
| SEN | 0.84 ± 0.08 | 0.86 ± 0.06 | 0.73 ± 0.29 | 0.86 ± 0.06 |
| PPV | 0.88 ± 0.08 | 0.88 ± 0.06 | 0.20 ± 0.14 | 0.86 ± 0.06 |
| HD | 2.60 ± 1.34 | 2.42 ± 1.03 | 11.47 ± 2.20 | 2.51 ± 1.47 |
| MSD | 0.22 ± 0.10 | 0.19 ± 0.08 | 3.63 ± 1.14 | 0.22 ± 0.12 |
3). Comparison With the State-of-the-Art Methods:
In this group of experiments, our proposed co-clustering method was compared with four mono-modal methods: 1) 3D-LARW [12], 2) the original ECM [53], 3) SECM [24], and 4) FCM-SW [23]. In addition, it was also compared with two co-segmentation methods: 5) a statistical method using hidden Markov tree model (denoted as HMT) [44], and 6) M2EDN [47], a CNN-based method implemented via using PET and CT as multi-channel inputs. For the supervised M2EDN method, the segmentation results were quantified by 10-fold cross validation. To train a reliable network in each iteration, the training data was augmented on-the-fly via random rotations and small distortions.
The quantitative results of all competing methods are summarized in Table II, from which we can have at least two observations. First, the co-segmentation methods (i.e., HMT, M2EDN, and our proposed method) yield overall better performance than the mono-modal methods (i.e., 3D-LARW, ECM, SECM, and FCM-SW), which demonstrates that the combination of anatomical CT information and functional PET information is beneficial for more accurate tumor segmentation. Second, our proposed co-clustering method outperforms the other two co-segmentation methods (i.e., HMT and M2EDN). This is mainly due to: 1) Capitalizing on the specific context term (i.e., (9)) and fusion strategy defined in the framework of BFT, our proposed method provides an effective way to improve the delineation of target tumor. 2) The performance of HMT and M2EDN may be hampered, respectively, by the difficulty in conjointly defining the distributions of PET and CT voxels, and the limited number of training samples for the construction of a deep neural network.
TABLE II.
Quantitative Results Obtained by Different Segmentation Methods on All The 21 Sets of PET-CT Images. The DSC, SEN, PPV, HD (in Voxel), and MSD (in Voxel) Are Presented as Mean±Standard Deviation
| 3D-LARW | ECM | SECM | FCM-SW | HMT | M2EDN | Our method | |
|---|---|---|---|---|---|---|---|
| DSC | 0.80 ± 0.08 | 0.72 ± 0.14 | 0.77 ± 0.13 | 0.83 ± 0.09 | 0.84 ± 0.04 | 0.84 ± 0.07 | 0.87 ± 0.04 |
| SEN | 0.76 ± 0.15 | 0.92 ± 0.07 | 0.84 ± 0.15 | 0.83 ± 0.11 | 0.83 ± 0.11 | 0.88 ± 0.11 | 0.86 ± 0.06 |
| PPV | 0.88 ± 0.09 | 0.63 ± 0.21 | 0.78 ± 0.23 | 0.88 ± 0.15 | 0.87 ± 0.11 | 0.83 ± 0.14 | 0.88 ± 0.06 |
| HD | 5.48 ± 5.48 | 5.96 ± 4.76 | 4.99 ± 3.78 | 3.98 ± 3.42 | 2.78 ± 1.00 | 3.58 ± 2.65 | 2.42 ± 1.03 |
| MSD | 0.55 ± 0.53 | 0.71 ± 0.69 | 0.54 ± 0.35 | 0.36 ± 0.29 | 0.26 ± 0.07 | 0.33 ± 0.19 | 0.19 ± 0.08 |
To be more comprehensive, the visual examples obtained by all competing methods are also presented in Fig. 5 for comparison. The first column of Fig. 5 presents the axial slices of four different tumors, where the first row is a slice corresponds to a large tumor, the second row represents a relatively small tumor, the third row represents a smaller tumor, and the last row represents a heterogenous tumor. The second column to the last column of Fig. 5 compare the contours delineated by different methods (green line) with those delineated by clinicians (blue line). We can observe that the contours delineated by the proposed method (the last column) are more consistent with the reference contours.
Fig. 5.

Contours delineated by different methods (from the second column to the last column) for four different tumor volumes shown in the axial plane. The first column represents the input images. The contours delineated by the automatic/semi-automatic methods (green lines) are compared with those by clinicians (blue lines) in the following columns.
Furthermore, it is worth mentioning that the segmentation results presented in this paper are also comparable to previous PET-CT co-segmentation studies. For example, our method yields DSC = 0.87 ± 0.04, which is comparable to Song et al. [33] (DSC = 0.81 ± 0.08), Ju et al. [36] (DSC = 0.84±0.06), Cui et al. [37] (DSC = 0.87±0.04), and Salah et al. [44] (DSC = 0.89 ± 0.13). It potentially implies that our proposed co-clustering method is a competitive alternative compared with existing co-segmentation methods.
V. Discussion
1). Effectiveness of textural features:
Our proposed method adopts textural features in addition to intensity-based features for the characterization of image voxels, and then in an unsupervised way, informative features are automatically selected to further determine a discriminant feature transformation for the co-clustering of PET and CT voxels. To evaluate its effectiveness, we alternatively removed textural features extracted based on GLSZM and GLCM, and compared the corresponding segmentation results with those obtained by using all extracted features. The quantitative comparison in terms of DSC, SEN, and PPV is shown in Fig. 6. We can observe that including textural features could effectively improve the performance of our method, e.g., DSC and PPV were increased, respectively, from 0.83 ± 0.06 to 0.87 ± 0.04 and 0.83 ±0.15 to 0.88 ± 0.06 in this group of experiments.
Fig. 6.
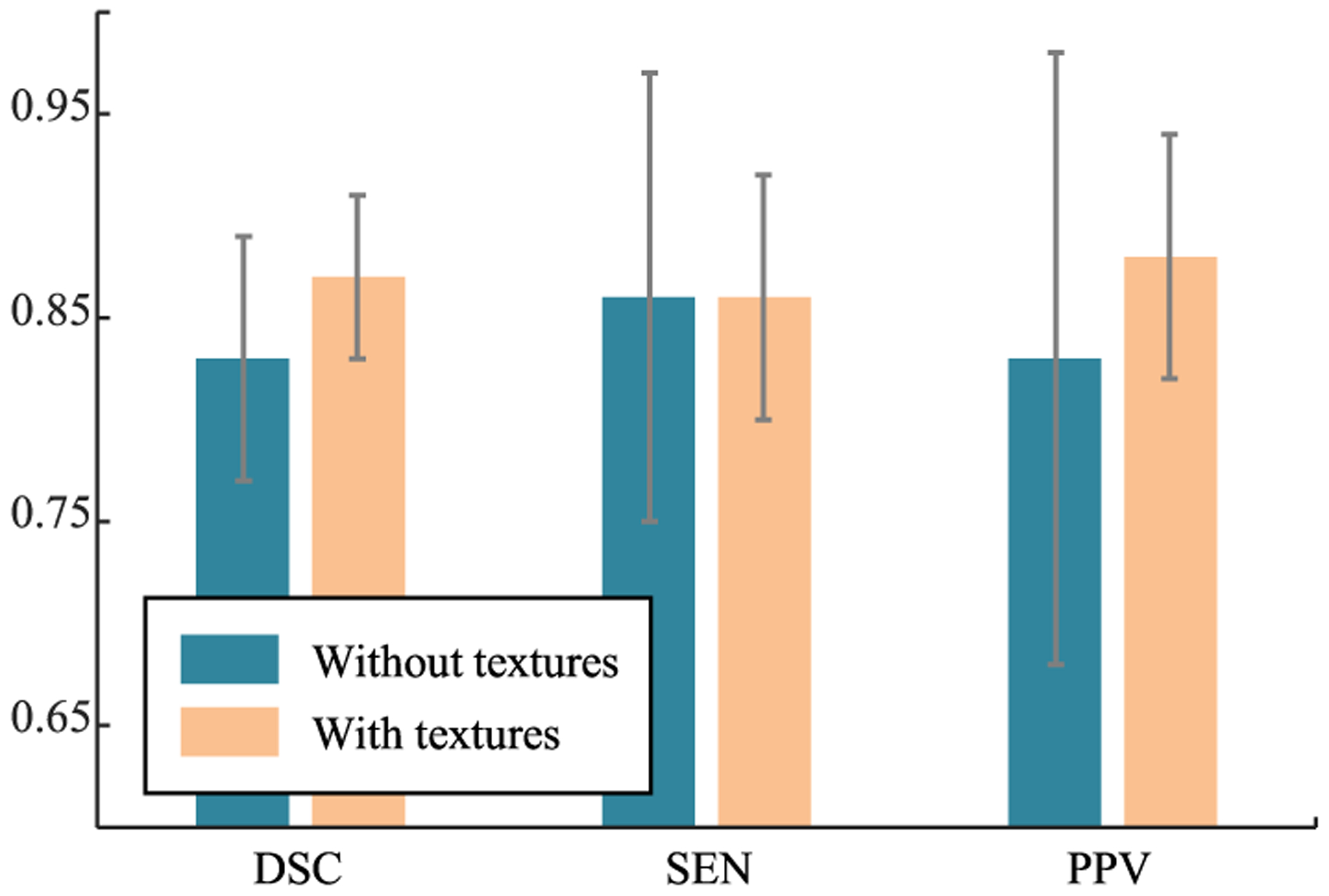
The quantitative segmentation results (in terms of DSC, SEN, and PPV) obtained by our proposed method with and without using textural features, respectively.
2). Effectiveness of information fusion based on Dempster’s rule:
To further refine the clustering results, the Dempster’s combination rule (3) was adopted in our method for the fusion of complementary knowledge from PET and CT images (i.e. Section III-C4), as well as the fusion of information from neighboring voxels (i.e. Section III-D). To evaluate the effectiveness of such fusion strategy, we excluded it from the proposed method. The corresponding segmentation results are then summarized in Table III, from which we can find that the fusion procedure could help to refine the final segmentations.
TABLE III.
Segmentation Performance of the Proposed Method, DSC and HD (in Voxel), With/Without the Fusion Procedure Based on Dempster’s Rule
| without fusion | with fusion | |
|---|---|---|
| DSC | 0.86 ± 0.04 | 0.87 ± 0.04 |
| HD | 2.62 ± 1.30 | 2.42 ± 1.03 |
3). Sensitivity to parameters:
As an illustration, we set γ to 0.001, and orderly chose a η and a λ from {0.001, …, 0.003, 0.07, 0.01, 0.03, …, 0.07, 0.1, 0.2} and {1, …, 10}, respectively. Then, the proposed method was applied to segment a relatively large tumor (volume of 135.80 mL) and a relatively small tumor (volume of 7.60 mL). The obtained DSCs are summarized in Fig. 7. We can observe that the obtained DSCs as a function of λ is relatively stable in a wide range. On the other hand, for the relatively large tumor, our method had better performance with small η; while, on the contrary, large η is better for the relatively small tumor.
Fig. 7.
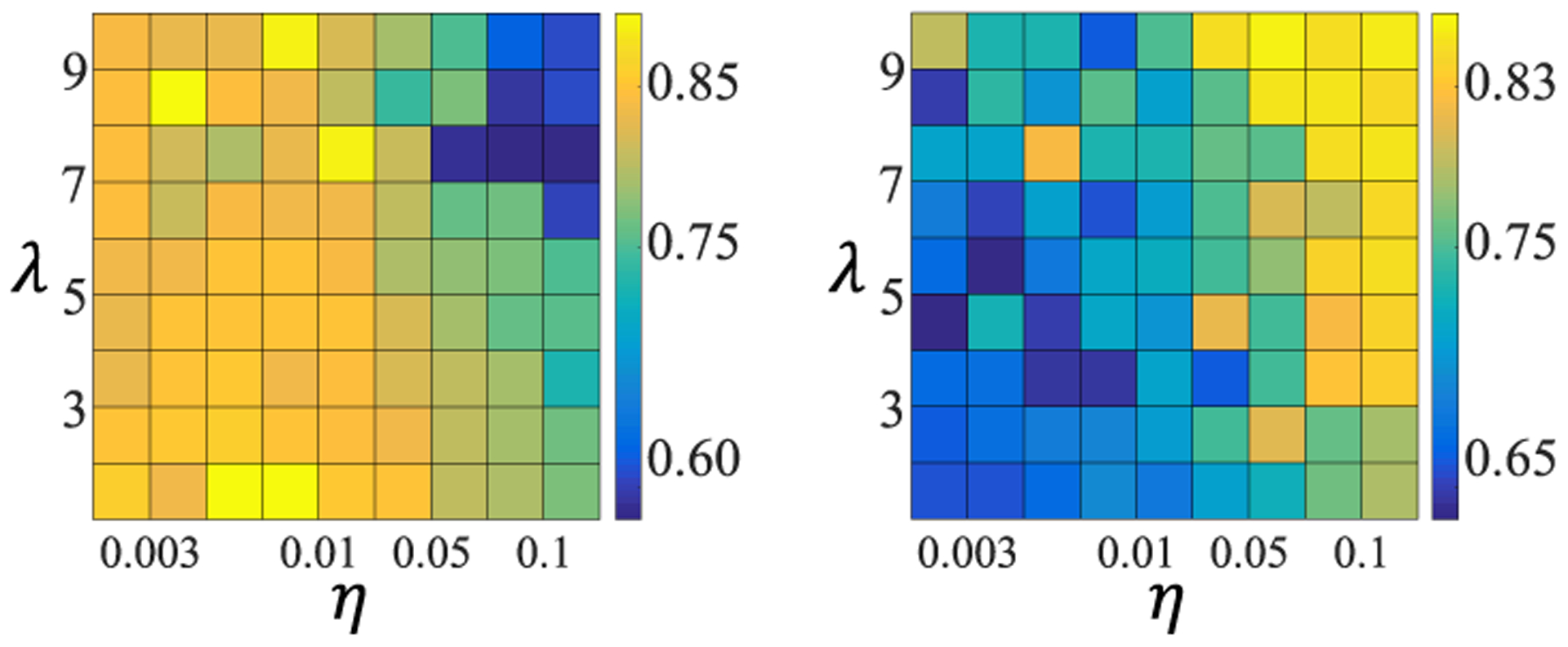
The DSC, namely the intensity value, as a function of λ and η. The first and the second column correspond to two tumors with the size of 135.80 mL and 7.60 mL, respectively.
VI. Conclusion
In this study, a novel co-clustering algorithm based on BFT has been proposed to jointly segment tumors in PET-CT images. Image voxels have been described not only by intensities but also by complementary textural features. For reliable clustering of image voxels in both PET and CT images, a specific spatial regularization and distance metric adaptation procedure have been included in the proposed method. A specific context term has been proposed in the framework of belief functions to encourage consistent segmentation between the two distinct mono-modalities. To effectively combine complementary information in PET and CT images, during the minimization of the constructed cost function, clustering results in the two mono-modalities have been iteratively adjusted by fusing them via the Dempster’s combination rule. The experimental results have shown that the proposed method performs well compared with existing monomodal segmentation methods and co-segmentation methods.
Biography

Chunfeng Lian received the B.S. degree in electronic and information engineering from Xidian University, Xi’an, China, in 2010, and the Ph.D. degree in computer science from the CNRS, Heudiasyc (UMR 7253), Univiersité de Technologie de Compiègne, Compiègne, France, in 2017. His current research interests include medical image analysis, machine learning, and pattern recognition.

Su Ruan received the M.S. and Ph.D. degrees in image processing from the University of Rennes, France, in 1989 and 1993, respectively. She was an Associate Professor with the University of Caen, France, from 1993 to 2003, and a Full Professor with the University of Champagne-Ardenne, France, from 2003 to 2010. She has been a Full Professor with the Université de Rouen Normandie, France, since 2010. Her main area of research is image processing, pattern recognition, information fusion, and medical imaging.

Thierry Denœux received the Graduate and Ph.D. degrees from the Ecole Nationale des Ponts et Chausseés, Paris, in 1985 and 1989, respectively. He is currently a Full Professor with the Université de Technologie de Compiègne, France. His research interest is the management of imprecision and uncertainty in data analysis, pattern recognition, and information fusion. He is a member of the Editorial Board of Fuzzy Sets and Systems and the Editor-in-Chief of the International Journal of Approximate Reasoning.

Hua Li received the Ph.D. degree from the Department of Electronics and Information Engineering, Huazhong University of Science and Technology, China, in 2001. She is currently an Assistant Professor with the Department of Radiation Oncology, Washington University in St. Louis, Saint Louis, USA. Her research interests include machine learning, pattern recognition, and image analysis techniques for applications in radiation therapy and diagnostic imaging.

Pierre Vera received the M.D. and Ph.D. degrees from Université Paris VI in 1993 and 1999, respectively. He is currently a University Professor and a Hospital Physician with the Faculty of Medicine, Université de Rouen Normandie, France. He is also the General Director of the Henri Becquerel Cancer Center, and the Head of the Department of Nuclear Medicine. His research interests include radiation oncology, nuclear medicine, biophysics, and medical imaging.
Contributor Information
Chunfeng Lian, CNRS, Heudiasyc, Sorbonne Universités, Université de Technologie de Compiègne, 60200 Compiègne, France, and also with the LITIS, QuantIF, Université de Rouen Normandie, 76130 Rouen, France.
Su Ruan, LITIS, QuantIF, Université de Rouen Normandie, 76130 Rouen, France.
Thierry Denœux, CNRS, Heudiasyc, Sorbonne Universités, Université de Technologie de Compiègne, 60200 Compiègne, France.
Hua Li, Department of Radiation Oncology, Washington University in St. Louis, Saint Louis, MO 63110 USA.
Pierre Vera, Department of Nuclear Medicine, Henri Becquerel Cancer Center, 76038 Rouen, France, and also with the QuantIF, LITIS, Université de Rouen Normandie, 76130 Rouen, France.
References
- [1].Vallières M, Freeman CR, Skamene SR, and El Naqa I, “A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities,” Phys. Med. Biol, vol. 60, no. 14, p. 5471, 2015. [DOI] [PubMed] [Google Scholar]
- [2].Lian C, Ruan S, Denœux T, Jardin F, and Vera P, “Selecting radiomic features from FDG-PET images for cancer treatment outcome prediction,” Med. Image Anal, vol. 32, pp. 257–268, August. 2016. [DOI] [PubMed] [Google Scholar]
- [3].Hatt M, Tixier F, Visvikis D, and Le Rest CC, “Radiomics in PET/CT: More than meets the eye?” J. Nucl. Med, vol. 58, no. 3, pp. 365–366, 2017. [DOI] [PubMed] [Google Scholar]
- [4].Foster B, Bagci U, Mansoor A, Xu Z, and Mollura DJ, “A review on segmentation of positron emission tomography images,” Comput. Biol. Med, vol. 50, pp. 76–96, July. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Hatt M et al. , “Classification and evaluation strategies of autosegmentation approaches for PET: Report of AAPM task group No. 211,” Med. Phys, vol. 44, no. 6, pp. e1–e42, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Vauclin S, Doyeux K, Hapdey S, Edet-Sanson A, Vera P, and Gardin I, “Development of a generic thresholding algorithm for the delineation of 18FDG-PET-positive tissue: Application to the comparison of three thresholding models,” Phys. Med. Biol, vol. 54, no. 22, 6901, 2009. [DOI] [PubMed] [Google Scholar]
- [7].Jentzen W, Freudenberg L, Eising EG, Heinze M, Brandau W, and Bockisch A, “Segmentation of PET volumes by iterative image thresholding,” J. Nucl. Med, vol. 48, no. 1, pp. 108–114, 2007. [PubMed] [Google Scholar]
- [8].Li H et al. , “A novel PET tumor delineation method based on adaptive region-growing and dual-front active contours,” Med. Phys, vol. 35, no. 8, pp. 3711–3721, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Tan S, Li L, Choi W, Kang MK, D’Souza WD, and Lu W, “Adaptive region-growing with maximum curvature strategy for tumor segmentation in 18F-FDG PET,” Phys. Med. Biol, vol. 62, no. 13, p. 5383, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Abdoli M, Dierckx RAJO, and Zaidi H, “Contourlet-based active contour model for PET image segmentation,” Med. Phys, vol. 40, no. 8, 082507, 2013. [DOI] [PubMed] [Google Scholar]
- [11].Jaouen V et al. , “Variational segmentation of vector-valued images with gradient vector flow,” IEEE Trans. Image Process, vol. 23, no. 11, pp. 4773–4785, November. 2014. [DOI] [PubMed] [Google Scholar]
- [12].Onoma DP et al. , “Segmentation of heterogeneous or small FDG PET positive tissue based on a 3D-locally adaptive random walk algorithm,” Computerized Med. Imag. Graph, vol. 38, no. 8, pp. 753–763, 2014. [DOI] [PubMed] [Google Scholar]
- [13].Mi H, Petitjean C, Vera P, and Ruan S, “Joint tumor growth prediction and tumor segmentation on therapeutic follow-up PET images,” Med. Image Anal, vol. 23, no. 1, pp. 84–91, 2015. [DOI] [PubMed] [Google Scholar]
- [14].Beichel RR et al. , “Semiautomated segmentation of head and neck cancers in 18F-FDG PET scans: A just-enough-interaction approach,” Med. Phys, vol. 43, no. 6, pp. 2948–2964, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Geets X, Lee JA, Bol A, Lonneux M, and Grégoire V, “A gradientbased method for segmenting FDG-PET images: Methodology and validation,” Eur. J. Nucl. Med. Mol. Imaging, vol. 34, no. 9, pp. 1427–1438, 2007. [DOI] [PubMed] [Google Scholar]
- [16].Wanet M et al. , “Gradient-based delineation of the primary GTV on FDG-PET in non-small cell lung cancer: A comparison with thresholdbased approaches, CT and surgical specimens,” Radiotherapy Oncol, vol. 98, no. 1, pp. 117–125, 2011. [DOI] [PubMed] [Google Scholar]
- [17].Montgomery DW, Amira A, and Zaidi H, “Fully automated segmentation of oncological PET volumes using a combined multiscale and statistical model,” Med. Phys, vol. 34, no. 2, pp. 722–736, 2007. [DOI] [PubMed] [Google Scholar]
- [18].Hatt M, Le Rest CC, Turzo A, Roux C, and Visvikis D, “A fuzzy locally adaptive Bayesian segmentation approach for volume determination in PET,” IEEE Trans. Med. Imag, vol. 28, no. 6, pp. 881–893, June. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Dewalle-Vignion A-S, Betrouni N, Lopes R, Huglo D, Stute S, and Vermandel M, “A new method for volume segmentation of PET images, based on possibility theory,” IEEE Trans. Med. Imag, vol. 30, no. 2, pp. 409–423, February. 2011. [DOI] [PubMed] [Google Scholar]
- [20].Sharif MS, Abbod M, Amira A, and Zaidi H, “Artificial neural network-based system for PET volume segmentation,” J. Biomed. Imag, vol. 2010, August. 2010, Art. no. 105610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Berthon B, Marshall C, Evans M, and Spezi E, “ATLAAS: An automatic decision tree-based learning algorithm for advanced image segmentation in positron emission tomography,” Phys. Med. Biol, vol. 61, no. 13, p. 4855, 2016. [DOI] [PubMed] [Google Scholar]
- [22].Foster B et al. , “Segmentation of PET images for computer-aided functional quantification of tuberculosis in small animal models,” IEEE Trans. Biomed. Eng, vol. 61, no. 3, pp. 711–724, March. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Belhassen S and Zaidi H, “A novel fuzzy C-means algorithm for unsupervised heterogeneous tumor quantification in PET,” Med. Phys, vol. 37, no. 3, pp. 1309–1324, 2010. [DOI] [PubMed] [Google Scholar]
- [24].Lelandais B, Ruan S, Denœux T, Vera P, and Gardin I, “Fusion of multi-tracer PET images for dose painting,” Med. Image Anal, vol. 18, no. 7, pp. 1247–1259, 2014. [DOI] [PubMed] [Google Scholar]
- [25].Lapuyade-Lahorgue J, Visvikis D, Pradier O, Le Rest CC, and Hatt M, “SPEQTACLE: An automated generalized fuzzy C-means algorithm for tumor delineation in PET,” Med. Phys, vol. 42, no. 10, pp. 5720–5734, 2015. [DOI] [PubMed] [Google Scholar]
- [26].Lian C, Ruan S, Denœux T, Li H, and Vera P, “Spatial evidential clustering with adaptive distance metric for tumor segmentation in FDGPET images,” IEEE Trans. Biomed. Eng, vol. 65, no. 1, pp. 21–30, January. 2018. [DOI] [PubMed] [Google Scholar]
- [27].Krizhevsky A, Sutskever I, and Hinton GE, “ImageNet classification with deep convolutional neural networks,” in Proc. Adv. Neural Inf. Process. Syst, 2012, pp. 1097–1105. [Google Scholar]
- [28].Hatt M et al. , “The first MICCAI challenge on PET tumor segmentation,” Med. Image Anal, vol. 44, pp. 177–195, February. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Gribben H, Miller P, Hanna GG, Carson KJ, and Hounsell AR, “MAP-MRF segmentation of lung tumours in PET/CT images,” in Proc. IEEE Int. Symp. Biomed. Imag. (ISBI), Jun-Jul 2009, pp. 290–293. [Google Scholar]
- [30].Wojak J, Angelini ED, and Bloch I, “Joint variational segmentation of CT-PET data for tumoral lesions,” in Proc. IEEE Int. Symp. Biomed. Imag. (ISBI), April. 2010, pp. 217–220. [Google Scholar]
- [31].Mu W et al. , “A segmentation algorithm for quantitative analysis of heterogeneous tumors of the cervix with 18F-FDG PET/CT,” IEEE Trans. Biomed. Eng, vol. 62, no. 10, pp. 2465–2479, October. 2015. [DOI] [PubMed] [Google Scholar]
- [32].Han D et al. , “Globally optimal tumor segmentation in PET-CT images: A graph-based co-segmentation method,” in Proc. Biennial Int. Conf. Inf. Process. Med. Imag, in Lecture Notes in Computer Science, vol. 6801. Springer, 2011, pp. 245–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Song Q et al. , “Optimal co-segmentation of tumor in PET-CT images with context information,” IEEE Trans. Med. Imag, vol. 32, no. 9, pp. 1685–1697, September. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Bagci U et al. , “Joint segmentation of anatomical and functional images: Applications in quantification of lesions from PET, PET-CT, MRIPET, and MRI-PET-CT images,” Med. Image Anal, vol. 17, no. 8, pp. 929–945, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Xu Z, Bagci U, Udupa JK, and Mollura DJ, “Fuzzy connectedness image co-segmentation for hybrid PET/MRI and PET/CT scans,” in Computational Methods for Molecular Imaging, in Lecture Notes in Computational Vision and Biomechanics, vol. 22. Springer, 2015, pp. 15–24, doi: 10.1007/978-3-319-18431-9_2. [DOI] [Google Scholar]
- [36].Ju W, Xiang D, Zhang B, Wang L, Kopriva I, and Chen X, “Random walk and graph cut for co-segmentation of lung tumor on PET-CT images,” IEEE Trans. Image Process, vol. 24, no. 12, pp. 5854–5867, December. 2015. [DOI] [PubMed] [Google Scholar]
- [37].Cui H et al. , “Topology polymorphism graph for lung tumor segmentation in PET-CT images,” Phys. Med. Biol, vol. 60, no. 12, pp. 4893–4914, 2015. [DOI] [PubMed] [Google Scholar]
- [38].Soh LK and Tsatsoulis C, “Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices,” IEEE Trans. Geosci. Remote Sens, vol. 37, no. 2, pp. 780–795, March. 1999. [Google Scholar]
- [39].Zhang J, Liang J, and Zhao H, “Local energy pattern for texture classification using self-adaptive quantization thresholds,” IEEE Trans. Image Process, vol. 22, no. 1, pp. 31–42, January. 2013. [DOI] [PubMed] [Google Scholar]
- [40].Thibault G, Angulo J, and Meyer F, “Advanced statistical matrices for texture characterization: Application to cell classification,” IEEE Trans. Biomed. Eng, vol. 61, no. 3, pp. 630–637, March. 2014. [DOI] [PubMed] [Google Scholar]
- [41].El Naqa I et al. , “Concurrent multimodality image segmentation by active contours for radiotherapy treatment planning,” Med. Phys, vol. 34, no. 12, pp. 4738–4749, 2007. [DOI] [PubMed] [Google Scholar]
- [42].Yu H, Caldwell C, Mah K, and Mozeg D, “Coregistered FDG PET/CT-based textural characterization of head and neck cancer for radiation treatment planning,” IEEE Trans. Med. Imag, vol. 28, no. 3, pp. 374–383, March. 2009. [DOI] [PubMed] [Google Scholar]
- [43].Markel D et al. , “Automatic segmentation of lung carcinoma using 3D texture features in 18-FDG PET/CT,” Int. J. Mol. Imag, vol. 2013, January. 2013, Art. no. 980769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Salah HH-B et al. , “A framework based on hidden Markov trees for multimodal PET/CT image co-segmentation,” Med. Phys, vol. 44, no. 11, pp. 5835–5848, 2017. [DOI] [PubMed] [Google Scholar]
- [45].Lapuyade-Lahorgue J, Xue J-H, and Ruan S, “Segmenting multisource images using hidden Markov fields with copula-based multivariate statistical distributions,” IEEE Trans. Image Process, vol. 26, no. 27, pp. 3187–3195, July. 2017. [DOI] [PubMed] [Google Scholar]
- [46].Kamnitsas K et al. , “Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation,” Med. Image Anal, vol. 36, pp. 61–78, February. 2017. [DOI] [PubMed] [Google Scholar]
- [47].Lian C et al. , “Multi-channel multi-scale fully convolutional network for 3D perivascular spaces segmentation in 7T MR images,” Med. Image Anal, vol. 46, pp. 106–117, May 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Shafer G, A Mathematical Theory of Evidence, vol. 1. Princeton, NJ, USA: Princeton Univ. Press, 1976. [Google Scholar]
- [49].Li X, Dick A, Shen C, Zhang Z, van den Hengel A, and Wang H, “Visual tracking with spatio-temporal Dempster–Shafer information fusion,” IEEE Trans. Image Process, vol. 22, no. 8, pp. 3028–3040, August. 2013. [DOI] [PubMed] [Google Scholar]
- [50].Liu Z, Li G, Mercier G, He Y, and Pan Q, “Change detection in heterogenous remote sensing images via homogeneous pixel transformation,” IEEE Trans. Image Process, vol. 27, no. 4, pp. 1822–1834, April. 2018. [DOI] [PubMed] [Google Scholar]
- [51].Pieczynski W and Benboudjema D, “Multisensor triplet Markov fields and theory of evidence,” Image Vis. Comput, vol. 24, pp. 61–69, January. 2006. [Google Scholar]
- [52].Boudaren MEY, An L, and Pieczynski W, “Unsupervised segmentation of SAR images using Gaussian mixture-hidden evidential Markov fields,” IEEE Geosci. Remote Sens. Lett, vol. 13, no. 12, pp. 1865–1869, December. 2016. [Google Scholar]
- [53].Masson M-H and Denœux T, “ECM: An evidential version of the fuzzy C-means algorithm,” Pattern Recognit, vol. 41, no. 4, pp. 1384–1397, 2008. [Google Scholar]
- [54].Makni N, Betrouni N, and Colot O, “Introducing spatial neighbourhood in evidential C-Means for segmentation of multi-source images: Application to prostate multi-parametric MRI,” Inf. Fusion, vol. 19, pp. 61–72, September. 2014. [Google Scholar]
- [55].Liu Z, Pan Q, Dezert J, Han J-W, and He Y, “Classifier fusion with contextual reliability evaluation,” IEEE Trans. Cybern, vol. 48, no. 5, pp. 1605–1618, May 2018. [DOI] [PubMed] [Google Scholar]
- [56].Bi Y, Guan J, and Bell D, “The combination of multiple classifiers using an evidential reasoning approach,” Artif. Intell, vol. 172, no. 15, pp. 1731–1751, 2008. [Google Scholar]
- [57].Jiao L, Denœux T, and Pan Q, “A hybrid belief rule-based classification system based on uncertain training data and expert knowledge,” IEEE Trans. Syst., Man, Cybern. Syst, vol. 46, no. 12, pp. 1711–1723, December. 2016. [Google Scholar]
- [58].Li F, Li S, and Denœux T, “k-CEVCLUS: Constrained evidential clustering of large dissimilarity data,” Knowl.-Based Syst, vol. 142, pp. 29–44, February. 2018. [Google Scholar]
- [59].Liu Z-G, Pan Q, Dezert J, and Martin A, “Combination of classifiers with optimal weight based on evidential reasoning,” IEEE Trans. Fuzzy Syst, vol. 26, no. 3, pp. 1217–1230, June. 2018. [Google Scholar]
- [60].Jousselme A-L, Grenier D, and Bossé É, “A new distance between two bodies of evidence,” Inf. Fusion, vol. 2, no. 2, pp. 91–101, 2001. [Google Scholar]
- [61].Liu M and Zhang D, “Pairwise constraint-guided sparse learning for feature selection,” IEEE Trans. Cybern, vol. 46, no. 1, pp. 298–310, January. 2016. [DOI] [PubMed] [Google Scholar]
- [62].Lian C, Ruan S, and Denœux T, “Dissimilarity metric learning in the belief function framework,” IEEE Trans. Fuzzy Syst, vol. 24, no. 6, pp. 1555–1564, December. 2016. [Google Scholar]
- [63].Waltz RA, Morales JL, Nocedal J, and Orban D, “An interior algorithm for nonlinear optimization that combines line search and trust region steps,” Math. Program, vol. 107, no. 3, pp. 391–408, 2006. [Google Scholar]
- [64].Beck A and Teboulle M, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imag. Sci, vol. 2, no. 1, pp. 183–202, 2009. [Google Scholar]


