Abstract
Objective:
Hydrogel scaffolds have attracted attention to develop cellular therapy and tissue engineering platforms for regenerative medicine applications. Among factors, local mechanical properties of scaffolds drive the functionalities of cell niche. Dynamic mechanical analysis (DMA), the standard method to characterize mechanical properties of hydrogels, restricts development in tissue engineering because the measurement provides a single elasticity value for the sample, requires direct contact, and represents a destructive evaluation preventing longitudinal studies on the same sample. We propose a novel technique, acoustic force elastography microscopy (AFEM), to evaluate elastic properties of tissue engineering scaffolds.
Results:
AFEM can resolve localized and two-dimensional (2D) elastic properties of both transparent and opaque materials with advantages of being non-contact and non-destructive. Gelatin hydrogels, neat synthetic oligo[poly(ethylene glycol)fumarate] (OPF) scaffolds, OPF hydroxyapatite nanocomposite scaffolds and ex vivo biological tissue were examined with AFEM to evaluate the elastic modulus. These measurements of Young’s modulus range from approximately 2 kPa to over 100 kPa were evaluated and are in good agreement with finite element simulations, surface wave measurements, and DMA tests.
Conclusion:
The AFEM can resolve localized and 2D elastic properties of hydrogels, scaffolds and thin biological tissues. These materials can either be transparent or non-transparent and their evaluation can be done in a non-contact and non-destructive manner, thereby facilitating longitudinal evaluation.
Significance:
AFEM is a promising technique to quantify elastic properties of scaffolds for tissue engineering and will be applied to provide new insights for exploring elastic changes of cell-laden scaffolds for tissue engineering and material science.
Keywords: Acoustic force elastography microscopy, acoustic radiation force, reflected longitudinally polarized shear waves, optical coherence tomography, scaffold, tissue engineering
I. Introduction
The interactions of cells in vivo are via cell-cell and cell-extracellular matrix (ECM) communications, which occur over three-dimensional (3D) scales. It has become clear that cells are regulated by soluble signaling molecules as well as mechanical properties of the ECM [1]. In tissue engineering, hydrogel scaffolds present an artificial 3D micro-environment for encapsulated cells to mimic the native ECM micro-environment to support cell adhesion, proliferation, and migration [2, 3]. Scaffold mechanical properties have different requirements for each type of engineered tissue. For example, in the human body, brain tissue is soft with a Young’s modulus of 0.2–1 kPa, while bone tissue reaches a wide range of Young’s modulus values of 30 kPa up to 14 GPa [4] depending on the stage of development [5]. Additionally, mechanical properties of crosslinked scaffolds are driven by the physicochemical properties of the scaffolds’ individual constituents, as well as processing parameters such as material design, degree of crosslinking, and biodegradability. Recent findings have suggested that biofunctional cues that regulate cell activities can create the dynamic mechanical microenvironment for the cell-scaffold complex [6–8]. Scaffolds with specific compositions can drive cell differentiation towards preferred lineages for tissue engineering [7, 9]. Furthermore, the changes of stiffening behavior in scaffolds may affect the traction forces that cells apply to their matrix to alter the matrix [1], and correspond with the level of porosity and pore distribution [10]. An ideal engineered scaffold should have perfect integration with host tissues and be biocompatible [11], and its mechanical properties should be designed as close to native tissue as possible [12, 13]. Therefore, evaluating mechanical properties of scaffolds and monitoring their stiffness changes is critical in tissue engineering and biomaterial science.
Dynamic mechanical analysis (DMA) is the standard method to evaluate mechanical properties of scaffolds in tissue engineering [14, 15], which can be used to obtain the compression Young’s modulus under a uniaxial vertical load control or displacement control with a specific strain rate. DMA has been widely used to quantify the mechanical properties of scaffolds including collagen-glycosaminoglycan scaffolds [16], calcium phosphate scaffolds [3], hydrogel infused network silk scaffolds [17], chitosan-alginate scaffolds [18], porous polyurethane scaffolds [19] and zirconia scaffolds [20], and others. The major limitations of DMA tests are that they represent study endpoints because they are destructive and require many replicates of the scaffolds to monitor elastic changes of cell-laden scaffolds associated with their biodegradation, cell proliferation and mineralization in a longitudinal study. The other drawbacks of DMA tests are that they have low spatial resolution (global elasticity measurement for the sample) and require direct contact of the sample, which increases the risk of contamination of biological samples.
Atomic force microscopy (AFM) is another option to quantify mechanical properties of scaffolds [21–25]. The prominent advantage of AFM is that it can be directly performed on native specimens to characterize localized mechanical properties [26]. However, in tissue engineering, AFM is not a mainstream method for mechanical characterization of scaffolds due to its dependence on technical expertise and complicated calibration procedures, which dramatically increases the difficulty of evaluating mechanical parameters [27]. Moreover, additional models such as the Hertz or the Sneddon models are essentially needed for evaluating mechanical characterizations by fitting loading curves [1, 28]. A small, relative to the scaffold size, indentation depth (few hundreds nanometer scale) [29] and tiny contact area of probe tips may reflect superficial mechanical properties over a small region of the sample undergoing investigation and cannot provide information corresponding to the whole thickness of scaffolds [30]. AFM also has similar disadvantages to the DMA method such as the need to directly contact with samples, a continual force interaction between tip and sample many times may damage samples, the tip can stretch or even scratch the surface, and the interaction between tip and sample could generate contamination to biological materials, preventing their longitudinal inspection [31, 32], which leads to AFM not being well-suited for characterizing scaffolds in tissue engineering.
Acoustic microscopy is a mature tool that was reported as early as almost 40 years ago to evaluate the condition of materials [33]. Acoustic microscopy can detect flaws such as solder bumps defects, laminar cracks, delamination and solder bridging of integrated circuits (IC) [34]. In material sciences, it can be used to inspect grain boundaries, voids, bubbles and contaminants by an ultrasonic pulse from the transducer to probe the sample and monitors the reflected echoes from a series of time delays of the pulses induced after interacting with the internal structure [35]. Acoustic microscopy is capable of observing ages of red blood cells (RBCs) to achieve a rich contrast and high resolving power of acoustic microscopy once the center frequency reaches the GHz level [36]. In tissue engineering, it can be used to evaluate internal structures, heterogeneous regions and defects of bulk opaque scaffolds as well as other materials and biological tissues [37]. However, it might have limitations on the evaluation of transparent samples or direct evaluation of the shear mechanical properties of soft tissues.
Non-contact-based techniques to quantify mechanical properties of biological materials commonly use an ultrasound transducer as an excitation source to generate mechanical waves propagating inside materials, and either use the ultrasound transducer itself to receive the backscattered ultrasound signals and estimate the motion (called shear wave elastography, SWE) [38, 39] or use optical coherence tomography (OCT) to obtain backscattered optical data to estimate the particle displacements (called optical coherence elastography, OCE) [40–42]. For both methods, particle displacement information relies on scatterers as the critical component in biological samples so that the propagating mechanical waves can be measured. Also, the methods require samples to be relatively thick (> 0.5 mm) and to have a sufficient lateral extent (several millimeters) for accurately estimating wave velocities traveling in a lateral direction. In tissue engineering, hydrogel scaffolds can be transparent (no optical or ultrasound scatterers), the thickness of scaffolds are generally on the order of 0.1–1 mm, and have a limited spatial size. Consequently, existing non-contact techniques to characterize mechanical properties of scaffolds are not appropriate for tissue engineering.
In this study, we propose a novel elastography technique, acoustic force elastography microscopy (AFEM), to evaluate mechanical properties of thin materials such as hydrogel scaffolds over a two-dimensional (2D) region for tissue engineering. AFEM can be used to evaluate elastic properties of transparent samples, i.e., scatterers in samples are not required as the essential component in the existing non-contact elastography measurements. Moreover, AFEM provides a higher elastography spatial resolution compared with DMA. Furthermore, the AFEM method does not directly contact the sample, which would allow for longitudinal studies within the same sample. To demonstrate and evaluate the AFEM method, we used tissue-mimicking gelatin hydrogels, oligo[poly(ethylene glycol)fumarate] (OPF) hydrogels, and OPF hydroxyapatite (HA) nanocomposite to examine the performance of the system. OPF is a polyethylene glycol (PEG)-derived macromer, and OPF hydrogels are biocompatible, nontoxic and can be cross-linked through the unsaturated double bond in the fumarate group and hydrolytically degraded through its ester bounds; therefore, OPF has appropriate properties for an ideal cell carrier for tissue engineering applications [43–46]. The development of AFEM can provide new insights to explore mechanical properties of scaffolds corresponded with cell differentiation, cross-linking densities, mineralization, biodegradation, and osteocalcin expression as examples in tissue engineering.
II. MATERIALS AND METHODS
A. Acoustic Force Elastography Microscopy (AFEM) and Reflected Longitudinally Polarized Shear Waves (RLPSWs)
AFEM consists of a highly focused ultrasound transducer, an optical coherence tomography (OCT) system and a x-y translation stage. In this study, a focused ultrasound transducer was used to produce the acoustic radiation force (ARF). The transducer was coupled to the bottom of the Petri dish using ultrasound coupling gel. The ARF was exerted on the surface of materials to generate surface waves that travel outwards on the surface as well as a wave that travels through the thickness of the material, which is defined as a longitudinally polarized shear waves (LPSWs) [47, 48], presented in Fig. 1. The waves that reflect from the bottom of the Petri dish and propagate back to the surface of materials are reflected LPSWs (RLPSWs). The arrival time, ta, of the RLPSW is determined by the local thickness of the sample, h, and shear modulus, μ, of the material according to the relationship , where ρ is the mass density of the material assumed as 1,000 kg/m3 for biological samples and the 0.5 factor accounts for the round-trip travel distance. Therefore, μ of the material can be given by ρ(0.5h/ta)2, where the term 0.5h/ta is defined as the velocity of RLPSWs, CAFEM. Young’s modulus E can be determined by E ≈ 3μ as the localized thickness h and ta of the material are obtained [49, 50], assuming that the material is isotropic, homogeneous, linear, and nearly incompressible. The spatial resolution of AFEM depends on a lateral focal size of the transducer that can be calculated by the equation: 2.44 × f/# × λUS and is approximately 510 μm in this study [51], where f/# is the f-number defined as the focal distance divided by the aperture size of the transducer and λUS is the ultrasound wavelength. Measurement of RLPSWs at the surface of materials do not require optical scatterers, i.e., materials can be transparent, which is common for hydrogel scaffolds in tissue engineering.
Fig. 1.
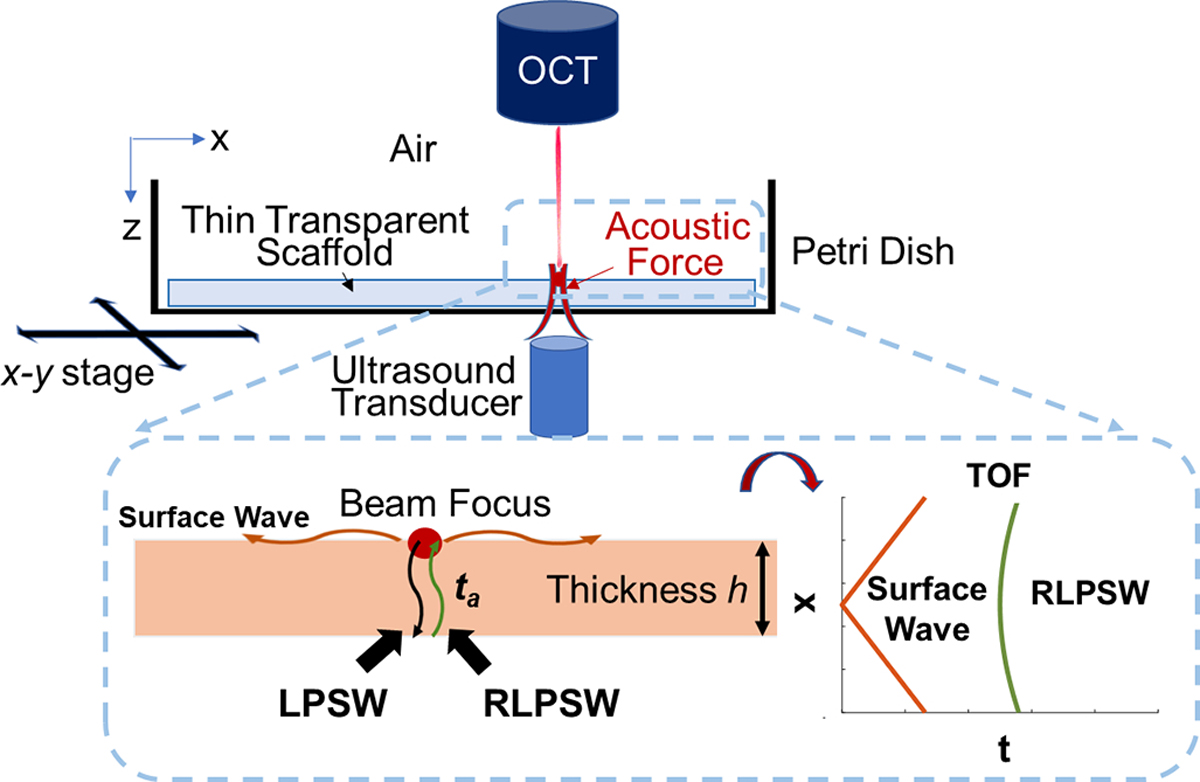
Principle of Acoustic Force Elastography Microscopy (AFEM). The LPSWs are generated by the acoustic radiation force, and the RLPSW traveling through the sample thickness h is detected at the surface by OCT. GM: galvanometer mirror, RF: radio frequency, LPSW: longitudinally polarized shear waves, RLPSW: reflected longitudinally polarized shear waves, OCT: optical coherence tomography, TOF: time-of-flight.
The role of the OCT in the AFEM system is to measure particle motion of RLPSWs. OCT has a number of advantages including being a non-contact measurement with micro-scale spatial resolutions, sensitivity to sensing particle displacements in nanometer scales with flexible scan speeds [52]; therefore, it is capable of supporting a finer elastography resolution in the AFEM system. Fig. 2 illustrates the basic optical layout of the spectral-domain optical coherence tomography (SD-OCT) system (TEL320C1, Thorlabs Inc., Newton, NJ, USA). The OCT is equipped with a 1300 nm source with low coherence broadband (236.8 nm of bandwidth) and LK4 lens kit (Thorlabs Inc., Newton, NJ, USA) to produce 20 μm of lateral resolution and 3.5 μm of z-axis resolution (provided by Thorlabs Inc.) in air. A low coherence broadband source is split into a reference beam directed toward a stationary reference mirror and a sample beam directed toward the samples. According to the basic principle of the Michelson interferometer, the back-reflected and back-scattered light from samples and retroreflected light from the reference mirror are recombined by a coupler. A spectral interferogram is formed by spectrometers and data are collected by a frame grabber card. The fast Fourier transform (FFT) is utilized to form an A-scan from the receiver array in the SD-OCT system. Each pixel includes a real value and an imaginary value (in-phase/quadrature, IQ) from which magnitude and phase can be calculated. One-dimensional (1D) autocorrelation was used to calculate the phase information Δφ of particle displacements including RLPSWs and surface waves [53]. The particle velocity of RLPSWs V(z, t) are given by [50, 54]
| (1) |
where fSR is the OCT scan rate, λOCT is center wavelength of light source and n is the refractive index of the material. Generally, the refractive index of biological materials, tissues and tissue-mimicking phantoms ranges from 1.35 to 1.55 [55, 56] and we selected 1.40 as an average value in the study.
Fig. 2.
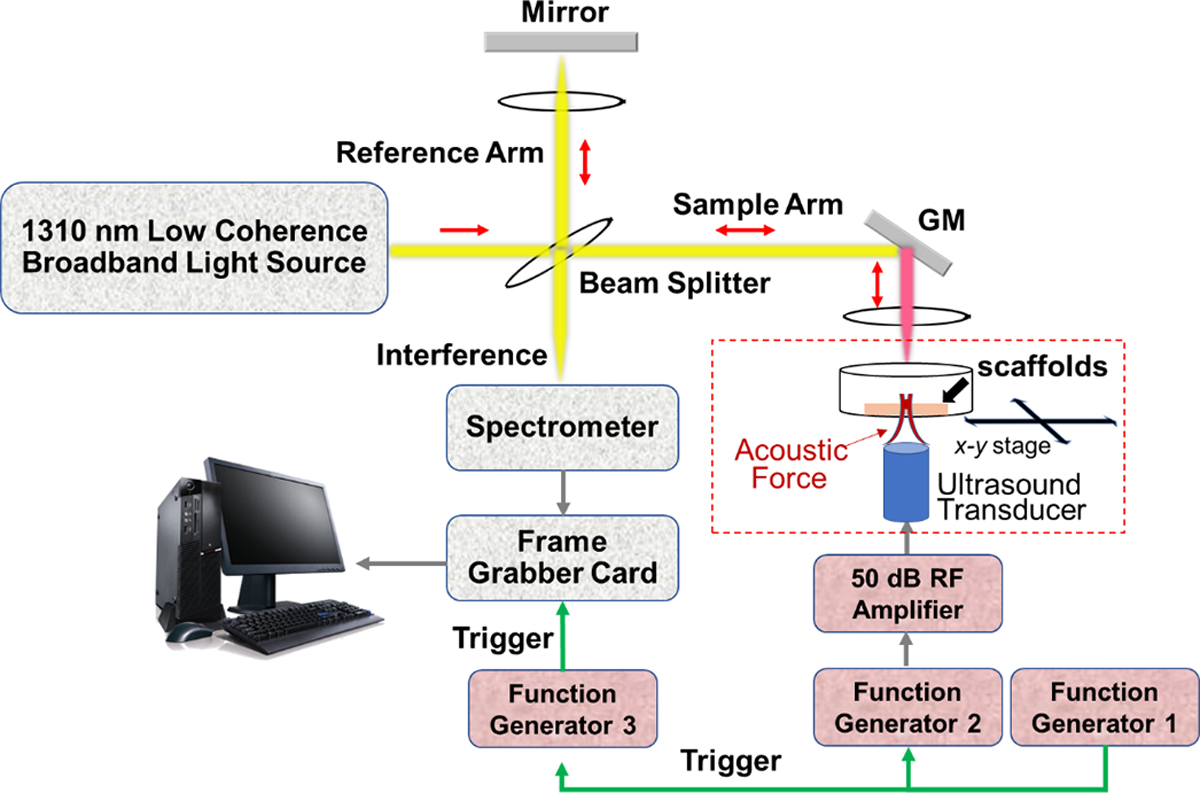
System structure of acoustic force elastography microscopy (AFEM). The three function generators are utilized to provide trigger and driving signals for synchronizing the AFEM scan (Function Generator 1), acoustic excitation (Function Generator 2) and recording signals with the OCT system (Function Generator 3). The details of red dashed rectangle are illustrated in Fig. 1 to explain the behaviors of LPSWs and RLPSWs. The LPSWs are generated by the acoustic radiation force and travel through a thin scaffold with thickness h. The RLPSWs are detected at the surface by OCT. GM: galvanometer mirror, RF: radiofrequency.
A 7.5 MHz focused ultrasound transducer with a f/# of 1.07 was used to produce the acoustic radiation force (ARF). Due to different scales of thickness between tissue-mimicking gelatin hydrogels and scaffolds of tissue engineering, a sinusoidal burst signal with two different pulse durations was used for gelatin hydrogels (500 μs) and for scaffolds (50 μs) to provide signals that could be tracked with sufficient amplitude, which was provided by function generator 2 (33250A, Agilent, Santa Clara, CA, USA). The burst signals were amplified 50 dB by a radiofrequency (RF) power amplifier (240L, Electronics and Innovation, LTD, Rochester, NY, USA) to drive the transducer. Function generator 3 (33500B, Keysight, Santa Rosa, CA, USA) controlled the OCT scan rates and triggering in the external mode. Function generator 1 (33250A, Agilent, Santa Clara, CA, USA) was a master trigger to synchronize the timing for the AFEM entire system.
For measuring tissue-mimicking gelatin hydrogels as the system test stage, the customized scan pattern in AFEM was designed to use a 50 kHz A-line OCT scan rate and 100 μm lateral spacing over a 16 mm field-of-view (FOV) (160 spatial locations) to record both a RLPSW and a surface wave in the first 50 ms after the excitation initiation. To achieve a two-dimensional (2D) elastography measurement of scaffolds in a fast manner for tissue engineering, the lateral spacing was chosen to cover a 2–4 mm FOV (20–40 spatial locations) for each spatial position so that AFEM can take data over a small patch centered about the excitation area for each spatial position to achieve a high throughput measurement with AFEM. The scan pattern of AFEM (Fig. 3) at each individual location, p, a data set was acquired with dimensions of z depth samples and N = i·j is the product of i M-scans and j B-scans (M-B scan) [57] for an elasticity measurement in each location. For 2D scans, the scan pattern was composed of a dataset with the dimensions of z by N by k by s matrix, where k and s are the number of lateral and elevational elastography measurement positions, respectively. The 2D AFEM measurement can reveal more details of the elastic properties of scaffolds in tissue engineering, especially for composite scaffolds due to heterogeneous properties. The customized acquisitions were developed by using a SpectralRadar software development kit (SDK) 4.4 Version provided by Thorlabs Inc. in Microsoft Visual C++ 2019 development environment (Microsoft, Redmond, WA).
Fig. 3.
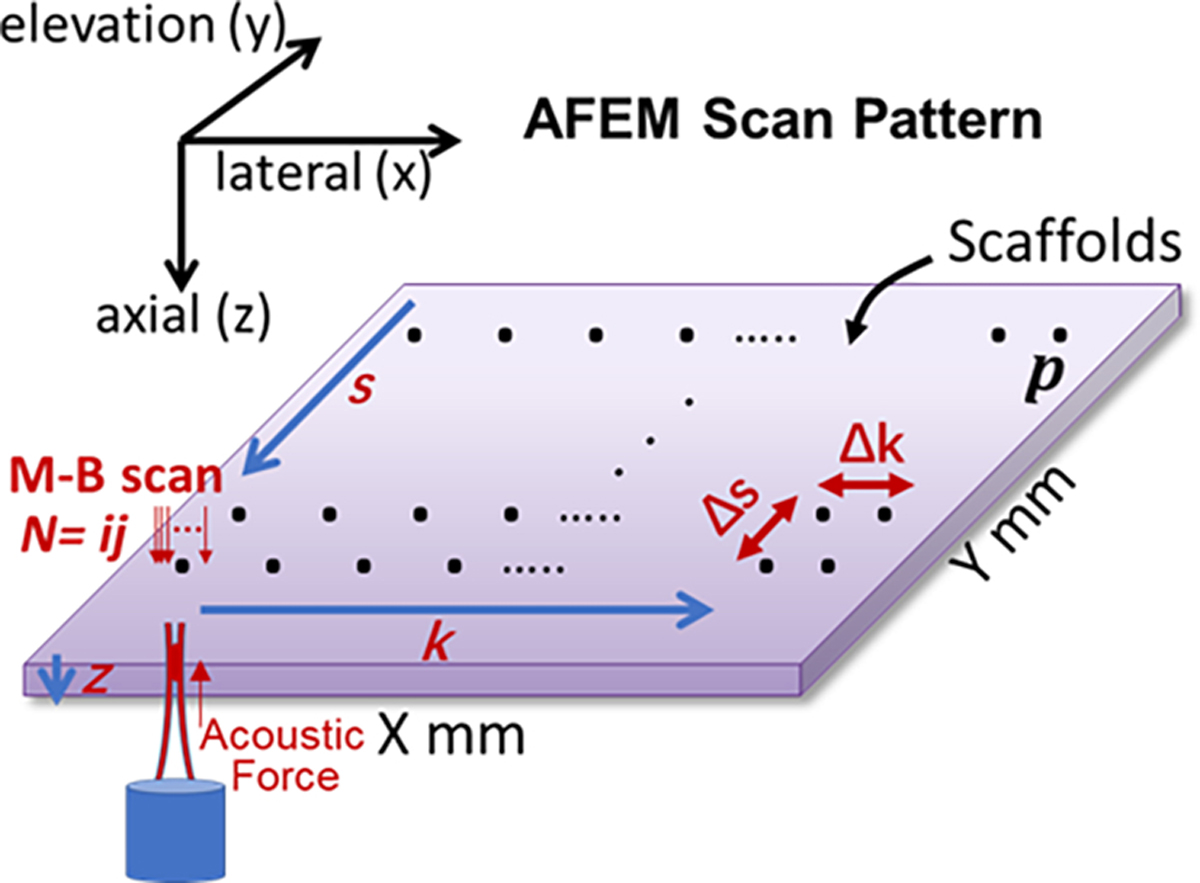
An illustration of the AFEM scan pattern. The elastography resolution in the lateral and elevational direction on a scaffold with X by Y mm scan range represents Δk and Δs, respectively. p: an individual elastography measurement position, i: the number of M-scans, j: the number of B-scans, z: depth, k: total scan numbers of lateral elastography measurement positions, s: total scan numbers of elevational elastography measurement positions, Δk: elastography resolution in the lateral direction, Δs: elastography resolution in the elevational elastography direction, X: sample width, Y: sample length.
B. Tissue-mimicking Gelatin Hydrogel Preparations
We fabricated nine gelatin hydrogels to conduct five independent experiments to evaluate the ability of AFEM. The first experiment was designed to study the behavior of RLPSWs. The second and third experiments were designed to evaluate AFEM performance with the fixed thickness and the fixed stiffness, respectively. The fourth experiment was designed to evaluate the elastic resolution of the AFEM. For the first experimental setup, a 20% v/v homogeneous gelatin hydrogel with 4.5 mm thickness was fabricated, with the thickness measured by a pulse-echo ultrasound test with 10 MHz single element transducer (V312, Olympus, Waltham, MA), by using gelatin powder (gel strength 300 type A, G2500-1KG, Sigma-Aldrich, St. Louis, MO, USA). One gram of titanium dioxide (TiO2, ReagentPlus ≥ 99%, Sigma-Aldrich, St. Louis, MO, USA) was used to provide optical scatterers for investigating the behaviors of RLPSWs compared with the results by the numerical simulation as the validation.
This comparison can evaluate two questions. First, can elastic properties be evaluated using RLPSWs? Second, can AFEM evaluate elastic properties of tissue-mimicking materials reliably? After the first experimental setup, surface waves were used as one of the validation methods, which were applied to the second and third experimental setups. The second experimental setup included the concentrations of 8% v/v, 13% v/v and 18% v/v gelatin hydrogels with the same thickness, 6 mm (measured by a pulse-echo ultrasound test), for the systematic study to evaluate the relationship between stiffness and RLPSW velocity. The third experimental setup was designed to evaluate the relationship between thickness and RLPSWs by using samples with thicknesses of 4.0, 3.2, and 2.5 mm, measured by a pulse-echo ultrasound test, with the same stiffness as 8% v/v. For each concentration, a total volume of 100 mL tap water in a 500 mL beaker was heated to approximate 70 °C. The gelatin powders and 1 g TiO2 were added with stirring to the beaker for approximately five minutes to homogenize the solution. The mixed solution was placed in a de-gassing chamber to remove small bubbles in the fluid. After de-gassing, the mixed gelatin solution was poured into regular Petri dishes (100 mm diameter × 10 mm height) and were transferred to a 4 °C refrigerator for 3 hours for congealing. The mechanical properties of the gelatin hydrogels with the room temperature were evaluated by the proposed AFEM.
The fourth experiment was performed to test the elastic resolution of the AFEM. A heterogenous gelatin hydrogel sample with high elastic contrast (10% v/v versus 20% v/v) was fabricated using gelatin powder (gel strength 300 type A, G2500-1KG, Sigma-Aldrich, St. Louis, MO, USA). Due to the advantage of AFEM, scatterers are not needed and the hydrogel can be completely transparent. For 20% gelatin hydrogel, a total volume of 100 mL tap water in a 500 mL beaker was heated to approximate 70 °C and the gelatin powders was added with stirring to the beaker for approximately five minutes to homogenize the solution. The gelatin solution was placed in a de-gassing chamber to remove small bubbles in the fluid and then was poured into a container (15 mm diameter × 10 mm height). The liquid gelatin hydrogel was transferred to a 4 °C refrigerator for 3 hours for congealing. After 3 hours, the above procedures were repeated for 10% gelatin hydrogel. The liquid gelatin hydrogel was poured into the same container to cover the substrate (20% gelatin hydrogel), which was transferred to a 4 °C refrigerator for the other 3 hours for congealing. Two planes with approximately 2 mm distance were sliced by using a tissue slicer blade to make a thin gelatin hydrogel sample.
The fifth experiment was performed to test whether or not the ARF pulse generates vibrations in the bottom of the Petri dish that influence the particle motion of RLPSWs. A 7% gelatin hydrogel was fabricated by the same procedure mentioned in the previous paragraph. The gelatin solution was poured into two Petri dishes, a regular Petri dish and a Petri dish where the bottom was replaced with Mylar film, with a volume of 15 mL in each to create the same thickness of the phantoms. The Mylar film is about 100 μm thick so the acoustic power is considered to be weakly attenuated [58]. The thickness of the phantom was measured as 2.053 mm by a pulse-echo ultrasound test. The material of the Petri dish is polystyrene and the thickness of the bottom is approximately 700 μm.
C. Numerical Simulations
To validate our proposed technique, numerical simulations were performed using the finite element method (FEM). An explicit solver was used to solve the differential elastic wave equations in OnScale (OnScale, Redwood City, California) using a transient excitation. Two three-dimensional models with elastic material properties were considered with 16 mm width × 4.5 mm thickness for the validation of the tissue-mimicking gelatin hydrogels and with 4 mm width × 950 μm thickness for the validation of the scaffolds for bone tissue engineering, respectively. By assuming that the Petri dish is infinitely stiffer than the tested samples, we can use a fixed displacement boundary condition applied at the bottom and sides of the numerical phantoms. The parameters of the numerical simulations were based on the results from the AFEM experiments.
According to the experimental results obtained by using AFEM, the RLPSW velocities in the 20% tissue-mimicking gelatin hydrogels and the neat OPF scaffold were set to be 2.28 m/s and 4.78 m/s, respectively. The simulation time step was 0.02 μs for the gelatin hydrogels and 0.0053 μs for the scaffolds due to the consideration of the sample thickness and the finite element size used. The Young’s modulus EAFEM can be approximately evaluated by [59], where CAFEM is the velocity of RLPSW and density of the materials ρ was set as 1000 kg/m3. A transient force excitation with the pulse duration of 500 μs (gelatin hydrogel) and with 50 μs (synthetic OPF scaffold) was applied to the surface of the model in an axial direction (red arrow of Fig. 2). Particle velocity motion data were measured from the top surface and further processed. The computation time for the numerical simulations took approximately 25 minutes using a standard personal computer (PC).
D. Porcine Kidney Tissue Preparation
A porcine kidney was excised immediately after sacrifice and frozen in saline. The pig was used for another study that was approved by the Mayo Clinic Institutional Animal Care and Use Committee. The kidney was thawed and placed in saline solution at room temperature. The kidney was sliced in half in the long dimension and reflected. A slice of renal cortex with approximate dimensions of 20 × 20 × 1.5 mm was cut for the experiment.
E. Fabrications of Synthetic Oligo[poly(ethylene glycol)fumarate] (OPF) Scaffolds and OPF Hydroxyapatite (HA) Nano-composite Scaffold for Tissue Engineering
Synthetic hydrogels have been widely used because of the ability to tailor their material properties such as molecular weight for specific tissue engineering applications. In this study, two groups of OPF scaffolds, the neat and composite OPF scaffolds with hydroxyapatite (HA), were fabricated. For each group, four samples were made, where one was used for AFEM measurement and the others were used for DMA tests as the validation. The OPF was synthesized from poly(ethylene glycol) (PEG) with a number average molecular weight (Mn) of 10,000 g/mol. A 50 g amount of PEG was azeotropically distilled in toluene to remove residual water. Dried PEG was dissolved in methylene chloride in a three-neck flask placed in the ice bath with nitrogen, which was followed by the addition of potassium carbonate (K2Co3) and distilled fumaryl chloride with 24 hours stirring. For the purification of the synthesized OPF, methylene chloride was removed by rotary evaporation and the resulting product was dissolved in ethyl acetate, precipitated in petroleum ether, cleaned with diethyl ether, and vacuum-dried overnight. For the neat OPF scaffolds, 0.5 g OPF, 0.15 g polyethylene glycol diacrylate (PEGDA) as a cross-linker and 2.5 mg Irgacure 2959 as a photo-initiator were dissolved in 1.15 ml deionized water (dH2O). For composite scaffolds, 10% w/w HA was fully dispersed in OPF solution before crosslinking. The solution was pipetted between glass-slides fitted with 1 mm thick Teflon spacer and transferred to cure the solution by a 365 nm UV light (Black-Ray Model 100AP, Upland, CA) at an intensity of 8 mW/cm2 for creating photo-crosslinked OPF scaffolds. The two-dimensional (2D) elastic properties of the crosslinked OPF scaffolds were characterized by AFEM, and their results were validated by conventional dynamic mechanical analysis (DMA) tests. The fabrication processes in more details can be found in previous reports [44, 45].
F. Dynamic Mechanical Analysis (DMA)
The neat OPF scaffolds and OPF composite scaffolds were cut into 8 mm diameter disks and subjected to compression under displacement control. The elastic properties of the scaffolds were determined using the RSA-G2 dynamic mechanical analysis (TA Instruments, New Castle, DE). The compression rate was set as 0.1 μm/s. The stress-strain data were collected from the tests and Young’s modulus E was determined by a slope of the linear portion of the stress-strain relationship in the 0–5% region.
G. Evaluation of AFEM elastography Spatial Resolution
Two planes with approximately 2 mm distance were sliced using a tissue slicer blade to make a thin gelatin hydrogel sample. A total of 21 measurements with a step of 0.635 mm were performed, and the 11th measurement was exactly at the boundary. AFEM was performed with a scan rate of 50 kHz with 50 μm lateral spacing. The duration of the acoustic excitation was 50 μs. The wave velocity profile was fit to a sigmoid function as an edge-spread function for the calculation of the elastography spatial resolution of AFEM based on the full-width at half-maximum (FWHM) of the differentiated edge-spread function.
III. RESULTS
A. AFEM Validation Using Finite Element Analysis and Dispersion Analysis
A 7.5 MHz focused ultrasound transducer with an f-number of 1.07 produced the acoustic radiation force (ARF). The ARF was exerted on the surface of materials to generate waves that travel through the thickness of materials, which are described as longitudinally polarized shear waves (LPSWs) [47, 48], as shown in Fig. 1. The wave that reflects from the bottom of the thin material due to the rigid boundary condition and vertically propagate back to the surface of the material through the same route are described as reflected LPSWs (RLPSWs). The mechanical properties of hydrogels and scaffolds are determined by two parameters: arrival time, ta, of the RLPSW and the thickness of the sample at the measuring location, h. Arrival time is defined as the time for waves to travel from the surface to the bottom and return back to the surface (Fig. 1). AFEM does not require optical scatterers, i.e., materials can be transparent, which is common for hydrogel scaffolds in tissue engineering.
The snapshots of the LPSW at 0.5 ms and the RLPSW at 4 ms vertically propagating inside a tissue-mimicking 20% gelatin hydrogel with 4.5 mm thickness were observed in Figs. 4(a) and 3(b) recorded by AFEM, respectively. Figures 4(a) and 4(b) clearly show the LPSW propagating from the surface of the phantom to the bottom of the Petri dish, and RLPSW exhibits a wave propagating back to the surface from the bottom of Petri dish (Movie S1). For a model with the same thickness and stiffness as in the AFEM experiments, the simulated wave motion was in a good agreement with the AFEM experimental results, illustrated in Figs. 4(c), 4(d) and Movie S2. According to the comparison between the numerical simulations and the measurement results by AFEM, three different types of wave velocities, the group velocity of surface waves Cg, the velocity of RLPSWs CAFEM, and the phase velocity of surface waves Cp, can be compared. The group velocity was evaluated by a time-to-peak algorithm across multiple lateral positions of spatiotemporal data (t-x), and phase velocity was calculated by transferring spatiotemporal data into a k-space (f-k) via 2D Fourier transform to obtain a frequency domain representation. The details of group and phase velocity calculation are provided in previous literature [60–62]. Figure 4(e) illustrates the spatiotemporal map containing the surface wave and the RLPSW measured by AFEM for the 20% gelatin hydrogel. In the first experimental setup, the field-of-view (FOV) of AFEM was set as the maximum view (16 mm) to record surface wave propagation for evaluating accurate results and comparing them with RLPSWs for validation. The Cg measured by AFEM was 2.28 m/s, which can be calculated by the slope of the wave indicated by the dark dashed line rectangle in Fig. 4(e). Using AFEM, ta was recorded as 4.03 ms and the thickness of the phantom was measured as 4.5 mm by a pulse-echo ultrasound test. The CAFEM was evaluated as 2.23 m/s and the Young’s modulus EAFEM was 14.91 kPa.
Fig. 4.
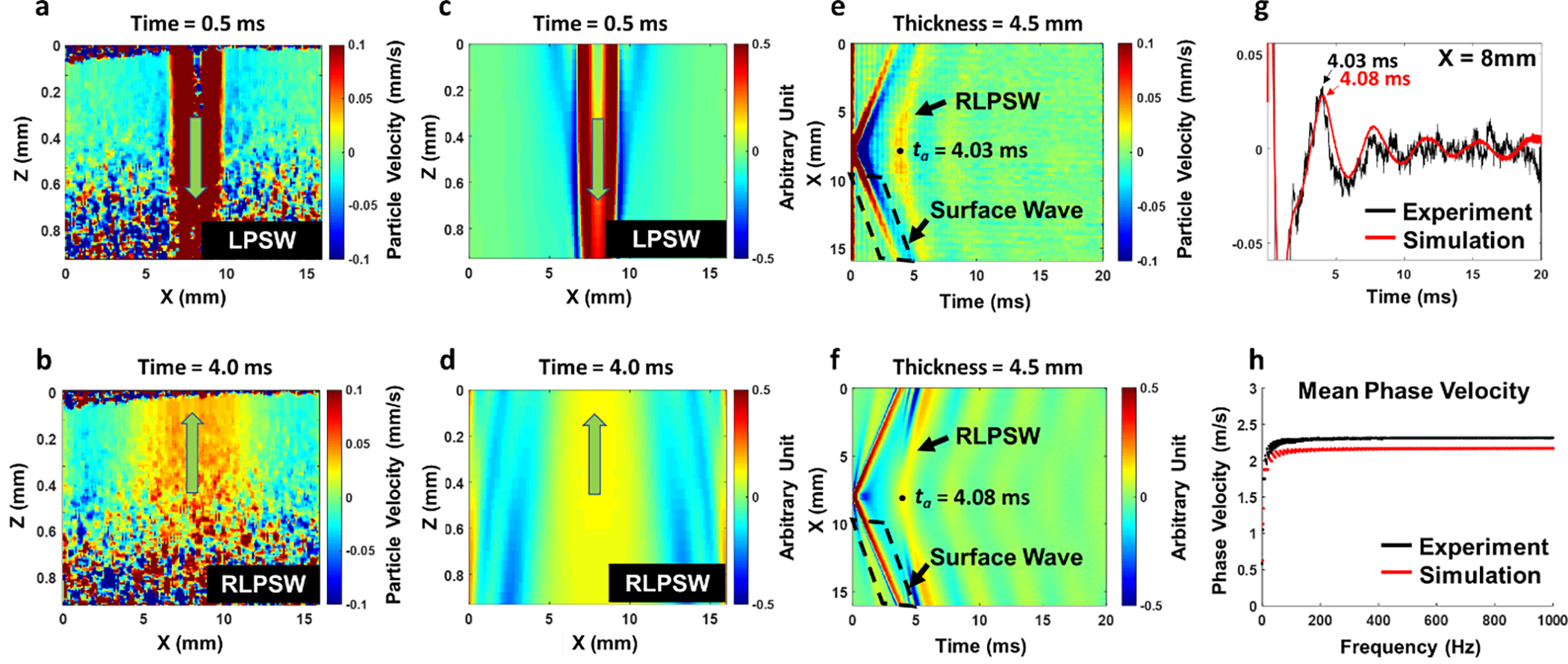
Numerical simulations compared with the AFEM results. Panels (a) and (b) illustrate the LPSW and the RLPSW, detected by AFEM, traveling vertically inside the 20% v/v tissue-mimicking gelatin phantom with 4.5 mm thickness, respectively. The video of the wave propagations can be found in the Movie S1. The LPSW and the RLPSW observed in the numerical simulation are presented in (c) and (d) in a material with the same mechanical properties of the 20% v/v gelatin phantom, respectively. The video of the numerical simulation is contained in Movie S2. Panels (e) and (f) show the spatiotemporal map from the experiment and the numerical simulation, respectively. The profiles selected at the excitation position indicated that the timing of RLPSW between the experiment and the simulation is highly consistent, shown in (g). Panel (h) illustrates the phase velocities calculated using the surface waves occurred on the 20% v/v gelatin phantom and the numerical simulation.
For the numerical simulations, the same elastic modulus (Cg = 2.28 m/s) and thickness (h = 4.5 mm) were used as the simulation parameters. According to the simulation results, Cg = 2.20 m/s, the ta = 4.08 ms and CAFEM = 2.21 m/s. The Young’s modulus based on the velocity of RLPSWs in simulations ESim was 14.65 kPa, presented in Fig. 4(f). A profile through the entire time dimension (20 ms) at the position of the ARF excitation was shown in Fig. 4(e). Figure 4(f) shows that the RLPSWs between the results measured by AFEM and the numerical simulations were highly consistent. The phase velocity dispersion curves of the experiment and the numerical simulations were displayed in Fig. 4(h) and mean Cp over a bandwidth of 200–1000 Hz is 2.31 ± 0.006 m/s for AFEM and 2.16 ± 0.005 m/s for the numerical simulation. According to the first experimental setup, the proposed AFEM has very good agreement with the numerical simulations. The Young’s modulus measured by using RLPSWs agreed well with those measured by using surface waves. The agreement from two independent methods gives high confidence in the quality of the proposed AFEM for evaluating the mechanical properties of biological samples.
B. Systematic Performance Evaluations of AFEM Using Tissue-mimicking Gelatin Hydrogels
Systematic evaluations of the performance of AFEM were performed using groups of tissue-mimicking gelatin hydrogels with the two design conditions, fixed thickness and fixed stiffness. In Figs. 5(a)–(c), with the fixed thickness of 6 mm, the RLPSWs can be clearly detected by AFEM with ta of 9.98 ms in 8%, 6.32 ms in 13% and 5.26 ms in 18% gelatin hydrogels demonstrating that ta is inversely proportional to the stiffness of the phantoms (Fig. 5d). In this experimental setup, the CAFEM changed from 1.32–2.32 m/s with increasing gelatin hydrogel concentrations (Table I). Consequently, EAFEM ranged from 5.25–16.14 kPa, presented in Fig. 5 and Table I, which implies that the mechanical properties are associated with the changes of CAFEM traveling in scaffolds. According to the results from the numerical simulations (Fig. 4), surface waves can be used to validate the results from AFEM. The FOV of AFEM was set as 16 mm to record surface wave propagation. According to Cg in Table I, the Young’s modulus based on surface waves ESurface ranging from 5.09–18.32 kPa show a highly consistent trend and a good agreement with EAFEM measurements.
Fig. 5.
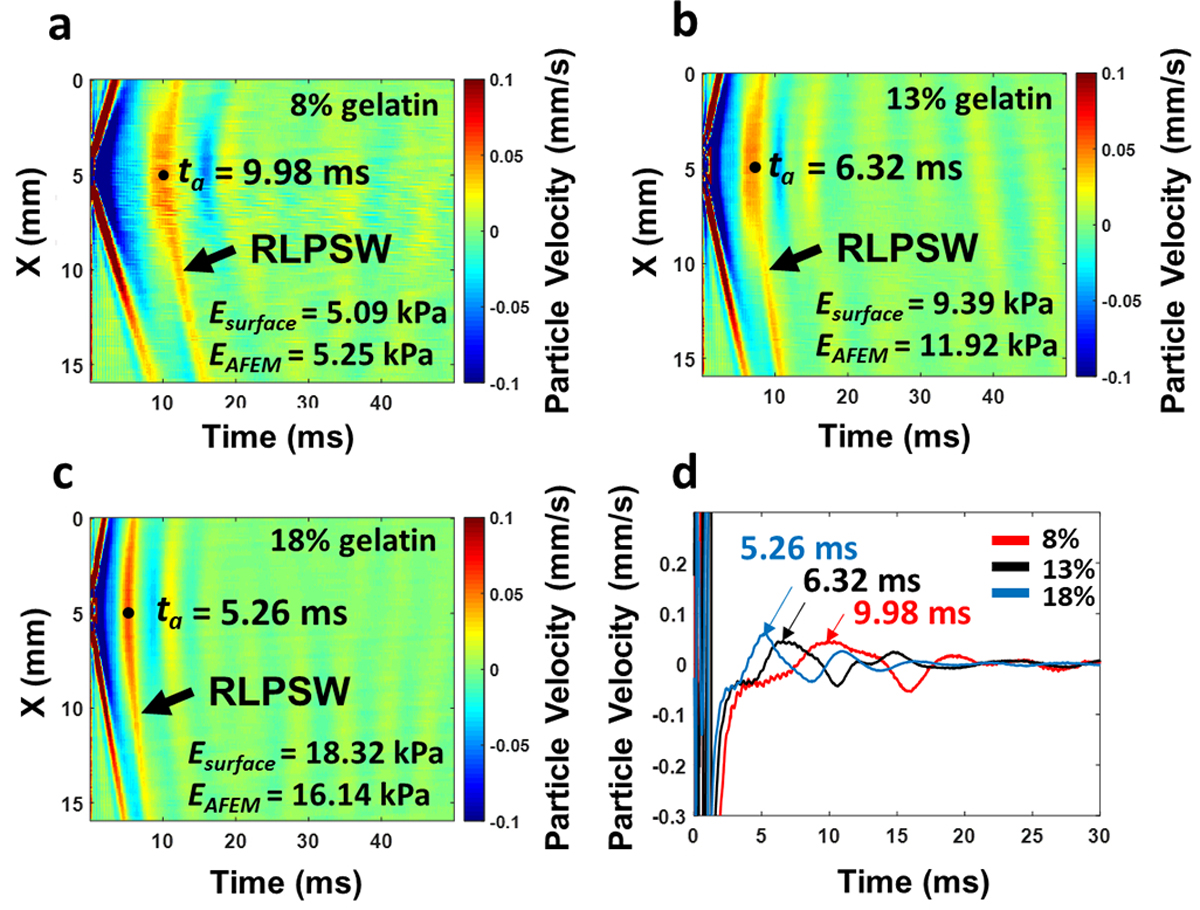
AFEM demonstrated on samples with fixed thickness. The RLPSWs were detected in (a) 8% v/v, (b) 13% v/v and (c) 18% v/v tissue-mimicking gelatin phantom with a constant thickness of 6 mm. The profiles selected at the excitation position indicated that the detected timing of RLPSWs is inversely proportional to the stiffness of the material, shown in (d).
TABLE I.
SUMMARY OF WAVE VELOCITIES AND ELASTIC MODULI OF ALL THE EXPERIMENTS
| Experiments | Velocity of RLPSWs (m/s) | Stiffness via RLPSWs (kPa) | Velocity of Surface Waves (m/s) | Stiffness via Surface Waves (kPa) | |
|---|---|---|---|---|---|
|
| |||||
| Test 1 | 20% Gelatin Hydrogel | 2.23 | 14.91 | G: 2.28 P: 2.31 (0.2-1.0 kHz) |
G: 15.59 |
| Simulation | 2.21 | 14.65 | G: 2.20 P: 2.16 (0.2-1.0 kHz) |
G: 14.52 | |
| Test 2 (fixed thickness) | 8% Gelatin Hydrogel | 1.32 | 5.25 | 1.30 | 5.09 |
| 13% Gelatin Hydrogel | 1.99 | 11.92 | 1.77 | 9.39 | |
| 18% Gelatin Hydrogel | 2.32 | 16.14 | 2.47 | 18.32 | |
| Test 3 (fixed stiffness) | 4.0 mm Gelatin Hydrogel | 0.96 | 2.85 | 0.93 | 2.59 |
| 3.2 mm Gelatin Hydrogel | 0.93 | 2.58 | 0.91 | 2.48 | |
| 2.5 mm Gelatin Hydrogel | 0.94 | 2.64 | 0.90 | 2.43 | |
| Porcine Kidney | 0.86 | 2.00 | 0.81 | 2.23 | |
| Neat OPF Scaffolds | 5.35 ± 0.07 | 86.14 ± 2.16 | DMA (kPa): 81.76 ± 7.35 | ||
| OPF 10% HA Nanocomposite Scaffolds | 6.16 ± 0.17 | 108.00 ± 5.98 | DMA (kPa): 102.80 ± 6.53 | ||
G = group velocity, P = phase velocity.
Figure 6 shows the RLPSWs in phantoms with three different thicknesses with a fixed stiffness (8% gelatin hydrogel) evaluated by AFEM. In Figs. 6(a)–(c), the RLPSWs were clearly detected by AFEM and ta is proportional to the thickness of the phantoms (Fig. 6(d)). In this experimental setup, the CAFEM stays constant at approximately 0.90 m/s regardless of thickness, with EAFEM ranging from 2.58–2.85 kPa for the three gelatin hydrogels, presented in Fig. 6 and Table I. The surface waves can be used for validating the AFEM experimental results. Using surface waves, the Cg and ESurface also show similar measurement values of approximately 0.90 m/s and 2.5 kPa in the three hydrogel phantoms, respectively. The two experimental setups demonstrate that AFEM is capable of evaluating the mechanical properties of materials with various thickness and stiffness. The systematic performance evaluations of AFEM with wave velocities and mechanical properties are summarized in Table I.
Fig. 6.
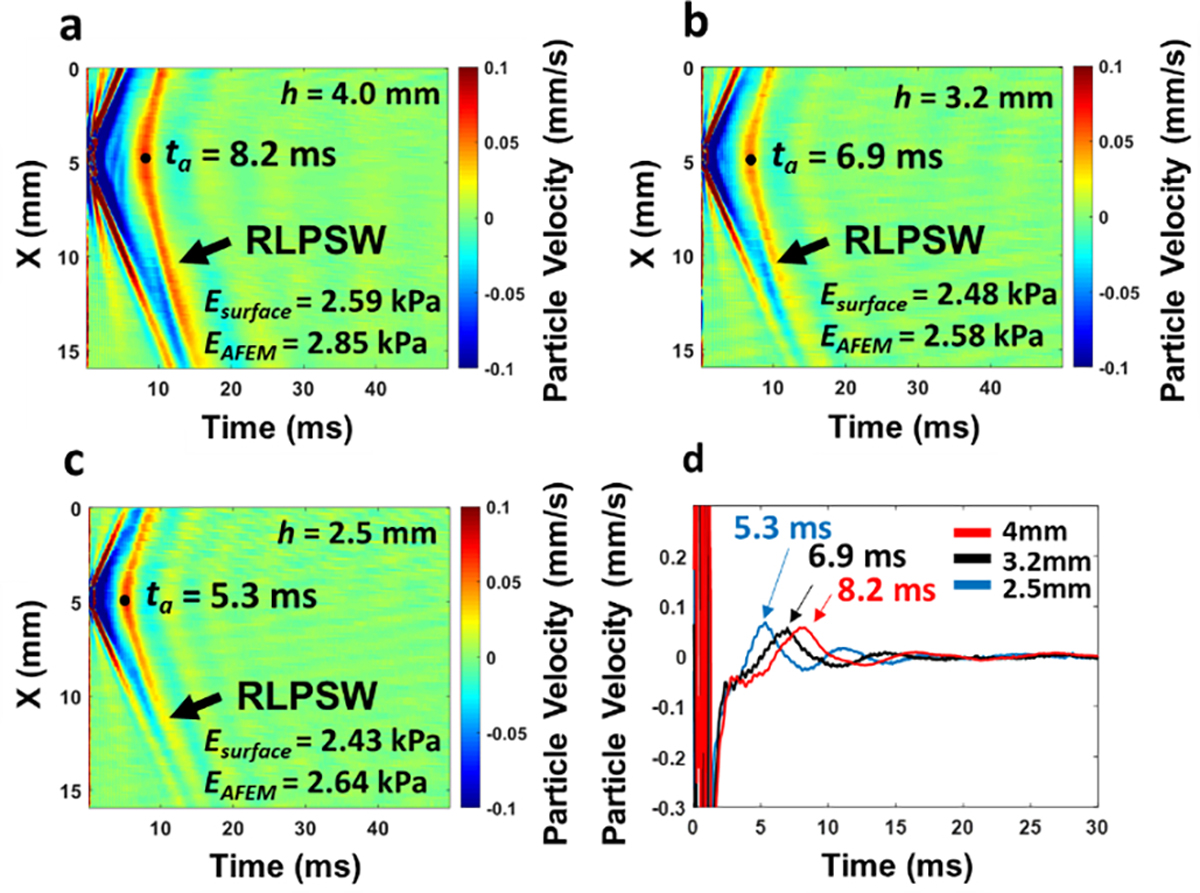
AFEM demonstrated on samples with fixed stiffness. The RLPSWs were detected in tissue-mimicking gelatin phantoms with varying thicknesses of (a) 4.0 mm, (b) 3.2 mm and (c) 2.5 mm while maintaining a constant stiffness with an 8% v/v gelatin concentration. The profiles selected at the excitation position indicated that the detected timing of RLPSWs is proportional to the thickness of the material, shown in (d).
C. Evaluation of Mechanical Properties of Ex vivo Porcine Kidney Using AFEM
We quantified the elastic properties of the ex vivo porcine kidney using AFEM. The porcine kidney cortex thickness of 1.53 mm can be determined from an OCT image as shown in Fig. 7(a). The RLPSWs propagating inside the porcine kidney and surface waves propagating on the porcine kidney sample were clearly detected by AFEM. The Cg was 0.86 m/s and ta of the RLPSW was 3.80 ms in Fig. 7(b). AFEM was repeated with ten acquisitions at the same location, and the ten profiles at the position of the ARF excitation is shown in Fig. 7(c). A consistent value of ta = 3.80 ms from ten RLPSWs was observed to demonstrate the stability of the RLPSWs as they are traveling inside tissue. The CAFEM was 0.81 m/s, which shows high consistency with Cg. The EAFEM and ESurface were approximately 2.00 kPa and was 2.23 kPa, respectively. Our previous literature reports that the Young’s modulus of ex vivo porcine kidney is around 2–3 kPa [63], which is in good agreement with the results measured by the proposed AFEM.
Fig. 7.
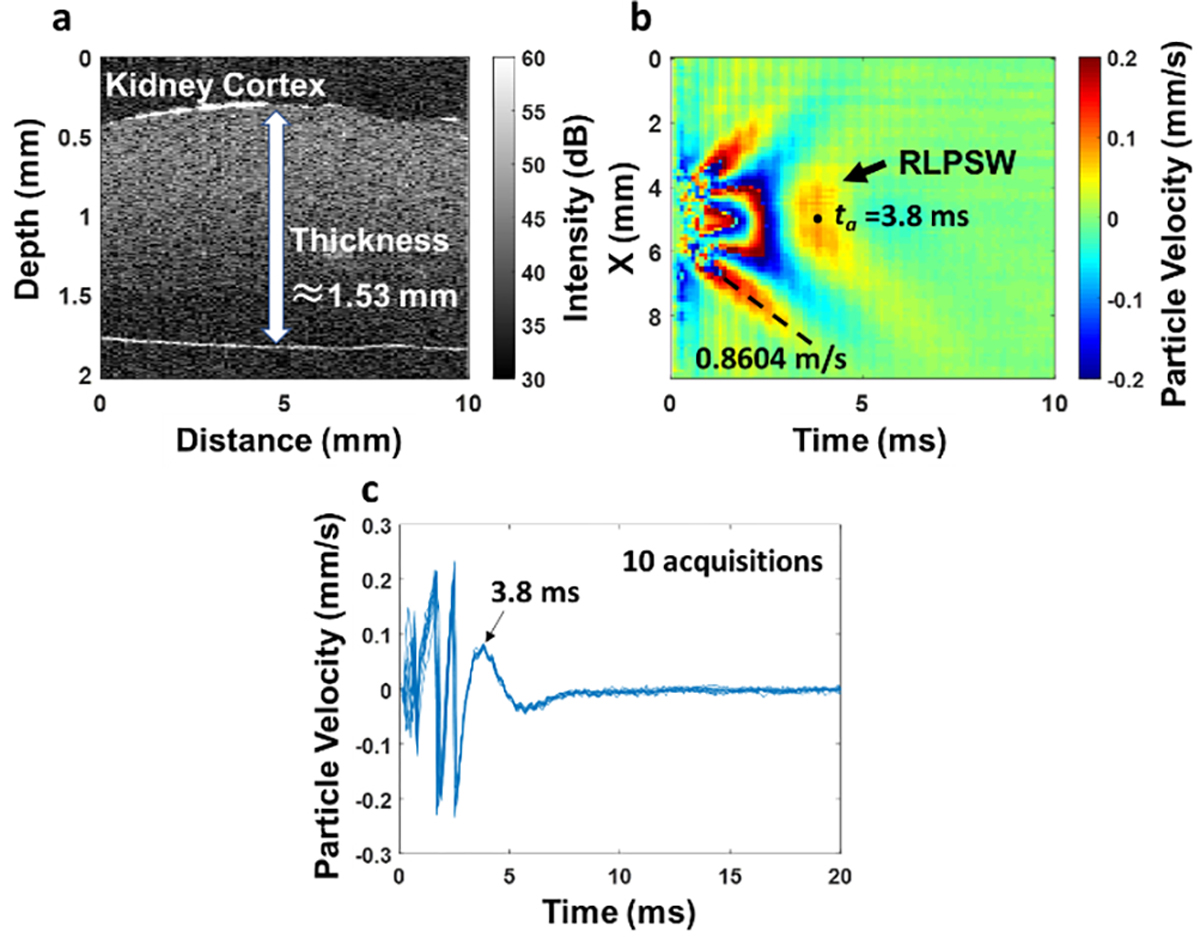
The elasticity measurement of porcine kidney tissue using AFEM. Panel (a) shows the porcine kidney cortex with the approximate 1.53 mm thickness as measured with OCT. The spatiotemporal map reveals the RLPSW and the surface wave propagating in the kidney tissue, presented in (b). The profiles from ten acquisitions at the same location indicate that the detected arrival time of RLPSWs is highly reproducible, shown in (c).
D. Evaluation of 2D Mechanical Properties of Neat OPF Scaffolds and OPF Hydroxyapatite (HA) Nano-composite Scaffolds for Tissue Engineering Using AFEM
To demonstrate the feasibility of the proposed AFEM for tissue engineering applications, the mechanical properties of the synthetic polymer scaffolds were evaluated. Figure 8 shows AFEM can characterize the stiffness of the neat OPF scaffold with Mn = 10,000 g/mol over a 2D region, and results were validated by numerical simulation and conventional DMA tests. In Fig. 8(a), the neat OPF scaffold can be observed as transparent, so it is difficult to quantify the elastic properties using conventional ultrasound and optical modalities due to the lack of scatterers. The thickness of the neat scaffold at a single position was measured to be approximately 960 μm, as shown in Fig. 8(b). The ta of the RLPSWs was 0.4 ms as detected by AFEM at the single position of the scaffold (Fig. 8(c)), and the CAFEM was evaluated as 4.78 m/s. The localized stiffness was determined as approximately 68.63 kPa for the neat scaffold and 66.21 kPa for the numerical simulation. According to the parameters of the scaffold thickness and CAFEM, the numerical simulation demonstrates that ta = 0.407 ms for the RLPSWs (Fig. 8(d)) is in accordance with the result from AFEM. AFEM has the ability to measure thickness, velocity of RLPSWs and mechanical properties of the scaffolds over a 2D region. The 2D maps consisted of 25 different scan positions (5 × 5 in x- and y-directions) with a 2.54 mm interval on the neat scaffold as shown in Fig. 8(a) with the dark red color region. The 2D maps of ta, h, and CAFEM of the scaffold are shown in Figs. 8(e)–(g). The ta over the 2D region was 0.31 ± 0.003 ms, h was 0.83 ± 0.006 mm and CAFEM was 5.35 ± 0.07 m/s. Therefore, the 2D elastic map of the neat scaffold measured using AFEM can be obtained as presented in Fig. 8(h), and EAFEM = 86.14 ± 2.16 kPa. Three repeated DMA tests were conducted to evaluate the Young’s modulus EDMA of the neat OPF scaffold as 81.76 ± 7.35 kPa, which shows good agreement with the AFEM results presented in Fig. 8(i).
Fig. 8.
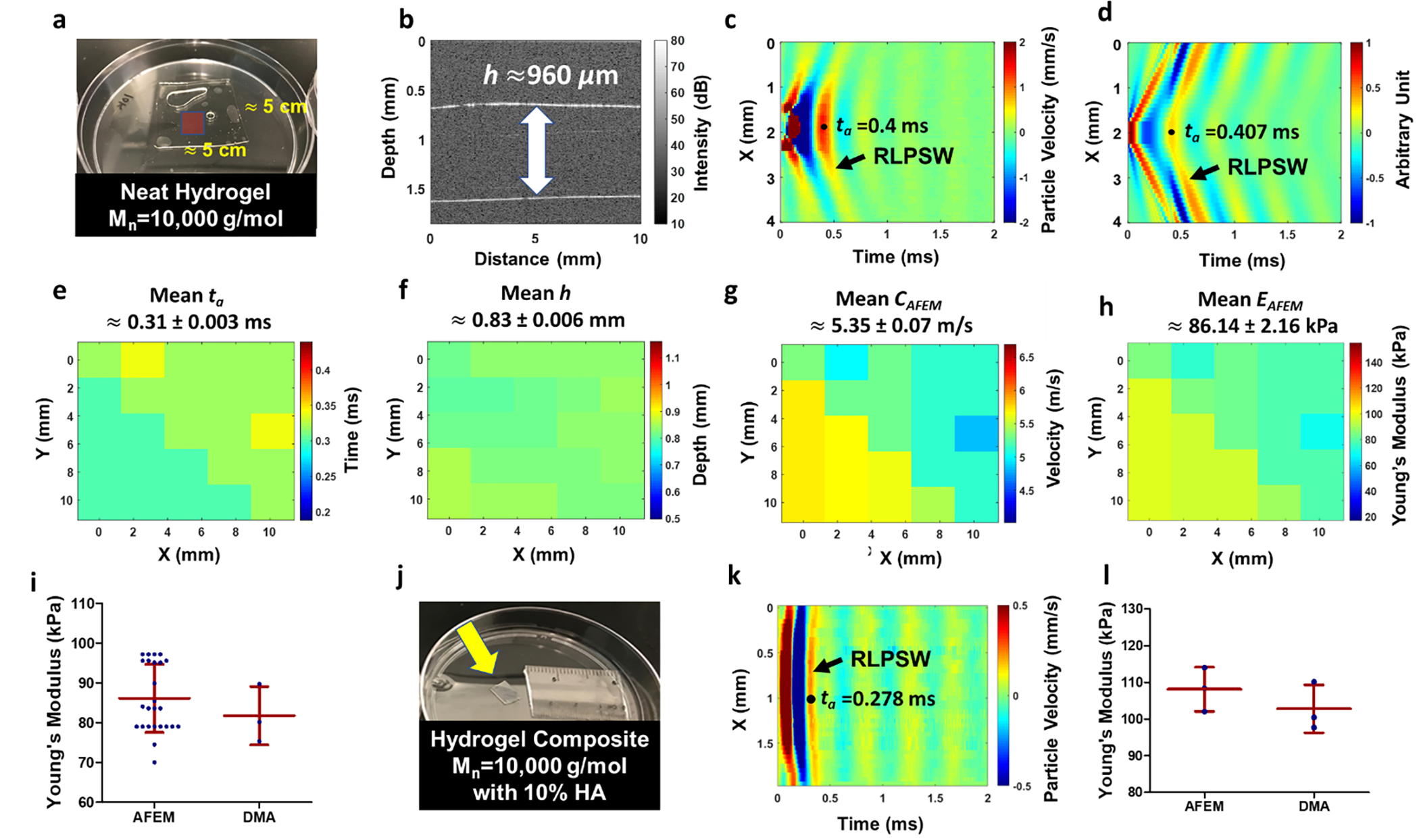
The 2D elasticity measurement of the neat transparent OPF scaffolds and OPF composite scaffolds with 10% w/w HA by using AFEM. Panel (a) shows a neat transparent OPF scaffold with Mn of 10,000 g/mol. (b) The thickness of the scaffold was imaged with OCT. Panels (c) and (d) show the RLPSW measured by AFEM and the numerical simulation result at a single position of the scaffold, respectively. (e) illustrates the reflected times of the RLPSWs with a total of 25 different locations (5 × 5 measurements in lateral and elevational direction with 2.54 mm elastography spacing) using AFEM. The scan range of the 2D measurement was approximately 12.7 mm × 12.7 mm, indicated as the rectangle with the dark red color in (a). The ta over the 2D region was 0.31 ± 0.003 ms. (f) displays the distribution of the thickness of the scaffold over the 2D region and the h was 0.83 ± 0.006 mm. The 2D CAFEM map was illustrated in (g) and CAFEM was 5.35 ± 0.07 m/s. In panel (h) the EAFEM of the scaffold was obtained and compared with the DMA results shown in (i). (j) An OPF composite scaffold with 10% w/w HA. (k) The RLPSW of the OPF composite scaffold at a single position was detected with AFEM. (l) The EAFEM from three measurements at the three different positions were obtained and compared the AFEM results with the DMA tests.
AFEM is also capable of evaluating the mechanical properties of composite scaffolds for tissue engineering. Figure 8(j) shows the OPF composite scaffold with 10% HA, which were examined by both AFEM and DMA. The h was 859 μm measured by AFEM and ta of the RLPSW was approximately 0.28 ms, as shown in Fig. 8(k); therefore, the CAFEM was 6.16 m/s and EAFEM was 114.00 kPa at a single location. Three measurements at randomly selected locations of the OPF composite scaffold were performed. The CAFEM and EAFEM of the OPF composite scaffolds were 6.16 ± 0.17 m/s and 108.00 ± 12.06 kPa by AFEM, respectively, which was validated by the DMA test with EDMA of 102.80 ± 6.53 kPa (Fig. 8(l)). The wave velocities and mechanical properties of scaffolds are summarized in Table I. The proposed AFEM technique is promising for quantitative mechanical characterization of thin scaffolds without scatterers and with non-contact and non-destructive measurements.
IV. DISCUSSION
Most mechanical characterization of scaffolds still relies on the DMA method for tissue engineering [3, 10, 15, 16]. Due to destruction of samples and the global nature of the elastic modulus measurement by using the DMA method, many important factors cannot be measured such as heterogeneity, elastic changes of cell-laden scaffolds associated with matrix mineralization and hydrogel degradations, which will be able to be addressed using AFEM. Recent research reported that mechanical properties of hydrogels can be determined by Brillouin spectroscopy at the sub-micron scale. However, the dimensions for the Brillouin spectroscopy measurement are relatively small with a 50 × 50 μm scale [64]. Additionally, Brillouin spectroscopy is generally applied only to transparent samples [65]. Although increasing the spectral extinction of virtually imaged-phase-array (VIPA)-based spectrometers can be a solution for evaluating non-transparent samples, improving signal-to-noise ratio (SNR) to an accepted range is still being explored [66]. The proposed AFEM can provide broad flexible measurement regions of the 2D mechanical properties from μm to cm spatial elastography scales in both transparent and non-transparent samples without extra processing.
The data for reconstruction of the 2D elasticity map could be acquired in a quick fashion with AFEM. For the 2D elasticity map in Fig. 8(h) as the example, the OCT A-line scan rate was set as 50 kHz and the lateral spacing was 100 μm over a 4 mm square FOV to increase the scan performance. For each location, the scan was repeated 500 times for an acquisition time of 10 ms. The data saving time from each complete scan at the single location was approximately 3 seconds, so the complete time for elastography measurement at a single location was 3.4 seconds. Therefore, the scan can be finished within approximately 1.5 minutes for a 2D elasticity map with 25 locations (5×5 in x- and y-directions with a 2.54 mm interval), which is far faster than DMA or AFM tests [45, 67] and demonstrates the high throughput performance of AFEM. Improved hardware could reduce this acquisition time further.
It is noted that the RLPSWs will be affected if the measurement position is adjacent to the boundary between materials with different elastic properties or the edge of a material. For the case when the measurement location is too close to the boundary with a large mechanical contrast, the AFEM spatial elastography resolution was approximately 720 μm as shown in Fig. 9. Therefore, keeping the distance of 720 μm between the measurement position and the edge of samples will contribute to accuracy of results in this particular instrument setup. However, using a higher frequency ultrasound with a smaller f-number may improve the spatial elastography resolution of the system.
Fig. 9.
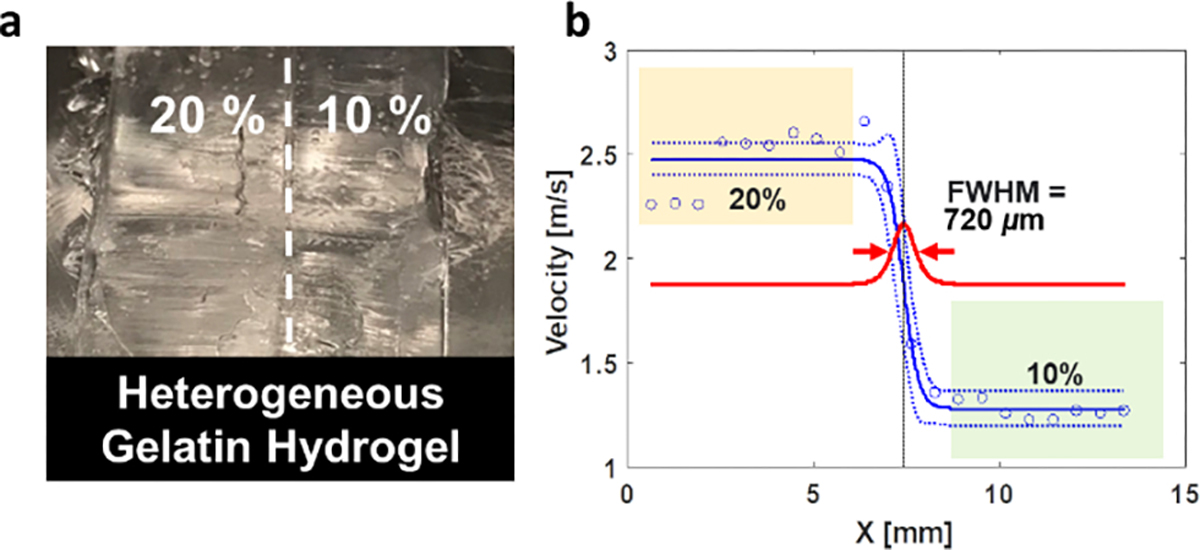
Evaluation of the elastography resolution of AFEM in a gelatin hydrogel with high mechanical contrast. Two planes with approximately 2 mm distance were sliced using a tissue slicer blade to make a thin gelatin hydrogel sample and boundary was indicated with white dash line, presented in (a). A total of 21 measurements with the step of 0.635 mm were performed and the 11th measurement was exactly at the boundary. The wave velocity profile was fit to a sigmoid function as an edge-spread function (b) for the calculation of the elastography spatial resolution of AFEM based on full-width half-maximum (FWHM) of the differentiated edge-spread function and the elastography spatial resolution was approximately evaluated as 720 μm.
We inspected if potential vibrations from the Petri dish will affect RLPSWs. Figure 10(a) illustrates the Petri dish with the bottom replaced by a Mylar film. The velocity of RLPSW CAFEM is 0.88 m/s for the phantom in the regular Petri dish and 0.84 m/s for the phantom in the Petri dish bottom replaced with Mylar film, presented in the Figs. 10(b) and 10(c). We also inspected the phase velocity of the surface wave propagating on the phantoms in two Petri dishes. The mean phase velocity with the standard deviation within the frequency range from 100–800 Hz is 0.82 ± 0.002 m/s for the phantom in the regular Petri dish and is 0.81 ± 0.019 m/s for the phantom in the Petri dish bottom replaced with Mylar film, presented in Fig. 10(d). The results of CAFEM and the phase velocity of the surface wave for the phantom in the regular Petri dish show a good agreement with those in the Petri dish bottom replaced with Mylar film. These results suggest that there may not be significant vibrations of the Petri dish bottom that affect the wave traveling on the surface of the phantoms and inside the scaffold material due to very stiff material. An additional explanation is that the ARF is focused on the surface of the tissue-mimicking material, and the ARF beam in the plastic material is not very intense due to being defocused.
Fig. 10.

Evaluation of the potential effects of the ARF causing vibration of the Petri dish bottom to influence RLPSW results in AFEM. Panel (a) shows a customized bottom with Mylar film. Panel (b) shows the RLPSW and the surface wave traveling in the gelatin hydrogel placed in the regular Petri dish and (c) placed in the Petri dish bottom replaced by a Mylar film. Panel (d) showed the phase velocity of the surface wave propagations on both phantoms.
In this work, we used samples with TiO2 scatterers to measure the wave motion at the surface and within the sample to understand the propagation of the LPSW and RLPSW. However, it should be noted that the AFEM method inherently only needs to make measurements at the surface of the material to characterize the arrival time of the RLPSW. Measurements in optically transparent samples are straightforward as the optical contrast between the air and solid material is typically strong.
The proposed AFEM has demonstrated several unique advantages: 1. There is no need for optical or acoustic scatterers, which means that transparent samples, common for hydrogel scaffolds for tissue engineering, can be studied; 2. The method does not require direct contact with samples; 3. AFEM does not require destruction of the samples; 4. AFEM can achieve higher spatial elastography resolutions to resolve both localized and 2D elastic properties with high throughput; 5. AFEM has the ability to provide flexible elastography measurement regions from μm to cm scales that can be controlled by the preference of users; and 6. The elastic properties of cell-laden scaffolds linked with polymer concentration, cross-linking densities, biodegradation rates, cell differentiation and degree of swelling in a longitudinal manner will be explored by using AFEM [68]. It also can be used to explore drug resistance regulated by matrix stiffness [69] and mechanogenomics mechanisms to explain the scaling of genome mutation rate with tissue stiffness for understanding cell infiltration [70] as examples. AFEM will be a powerful tool to quantify the mechanical properties of thin samples with non-contact manner and will be positively impact various fields such as biomedical technology, tissue engineering and biomaterials.
V. CONCLUSION
We proposed a new elastography technique, acoustic force elastography microscopy, to quantify the elastic properties of engineered transparent scaffold hydrogels as well as opaque tissue. We performed a number of experiments to examine the performance of AFEM including the tissue-mimicking gelatin hydrogels, porcine kidney tissue, neat OPF scaffolds and OPF composite scaffolds, which were validated by numerical simulations and DMA tests. AFEM will be a promising technique to provide new insights in tissue engineering and biomaterial science.
Supplementary Material
Acknowledgments
This work was supported in part by grant R01DK092255 from the National Institutes of Health (NIH). The authors thank Mrs. Jennifer L. Poston for administrative assistance.
Contributor Information
Hsiao-Chuan Liu, Department of Radiology, Mayo Clinic, Rochester, MN 55905, USA..
Bipin Gaihre, Department of Orthopedic Surgery, Mayo Clinic, Rochester, MN 55905, USA.
Piotr Kijanka, Department of Robotics and Mechatronics, AGH University of Science and Technology, Krakow 30059, Poland.
Lichun Lu, Department of Orthopedic Surgery, Mayo Clinic, Rochester, MN 55905, USA.
Matthew W. Urban, Department of Radiology, Mayo Clinic, Rochester, MN 55905, USA..
REFERENCES
- [1].Zhu Y et al. , “Determination of mechanical properties of soft tissue scaffolds by atomic force microscopy nanoindentation,” J Biomech, vol. 44, no. 13, pp. 2356–61, 2011. [DOI] [PubMed] [Google Scholar]
- [2].Shi C et al. , “Study on mechanical properties and permeability of elliptical porous scaffold based on the SLM manufactured medical Ti6Al4V,” PLoS One, vol. 16, no. 3, p. e0247764, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Fuentes E et al. , “Structural characterization and mechanical performance of calcium phosphate scaffolds and natural bones: a comparative study,” J Appl Biomater Biomech, vol. 8, no. 3, pp. 159–65, 2010. [PubMed] [Google Scholar]
- [4].Rho JY et al. , “Young’s modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements,” J Biomech, vol. 26, no. 2, pp. 111–9, 1993. [DOI] [PubMed] [Google Scholar]
- [5].Ghasemi-Mobarakeh L et al. , “Structural properties of scaffolds: Crucial parameters towards stem cells differentiation,” World J Stem Cells, vol. 7, no. 4, pp. 728–44, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Tran TT et al. , “A Review of Mechanical Properties of Scaffold in Tissue Engineering: Aloe Vera Composites,” Journal of Physics: Conference Series, vol. 1082, p. 012080, 2018. [Google Scholar]
- [7].Ghasemi-Mobarakeh L et al. , “Structural properties of scaffolds: Crucial parameters towards stem cells differentiation,” World Journal of Stem Cells, vol. 7, no. 4, pp. 728–744, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Howard D et al. , “Tissue engineering: strategies, stem cells and scaffolds,” J Anat, vol. 213, no. 1, pp. 66–72, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Elisseeff J et al. , “The role of biomaterials in stem cell differentiation: applications in the musculoskeletal system,” Stem Cells Dev, vol. 15, no. 3, pp. 295–303, 2006. [DOI] [PubMed] [Google Scholar]
- [10].Kim TR et al. , “Evaluation of structural and mechanical properties of porous artificial bone scaffolds fabricated via advanced TBA-based freeze-gel casting technique,” Appl Sci-Basel, vol. 9, no. 9, 2019. [Google Scholar]
- [11].Aliabouzar M et al. , “Acoustic and mechanical characterization of 3D-printed scaffolds for tissue engineering applications,” Biomed Mater, vol. 13, no. 5, p. 055013, 2018. [DOI] [PubMed] [Google Scholar]
- [12].Ebhodaghe SO, “Hydrogel-based biopolymers for regenerative medicine applications: a critical review,” Int J Polym Mater Po, pp. 155–172, 2020. [Google Scholar]
- [13].Mahinroosta M et al. , “Hydrogels as intelligent materials: A brief review of synthesis, properties and applications,” Mater Today Chem, vol. 8, pp. 42–55, 2018. [Google Scholar]
- [14].Gentleman E et al. , “Mechanical characterization of collagen fibers and scaffolds for tissue engineering,” Biomaterials, vol. 24, no. 21, pp. 3805–13, 2003. [DOI] [PubMed] [Google Scholar]
- [15].Lin AS et al. , “Microarchitectural and mechanical characterization of oriented porous polymer scaffolds,” Biomaterials, vol. 24, no. 3, pp. 481–9, 2003. [DOI] [PubMed] [Google Scholar]
- [16].Harley BA et al. , “Mechanical characterization of collagen-glycosaminoglycan scaffolds,” Acta Biomater, vol. 3, no. 4, pp. 463–74, 2007. [DOI] [PubMed] [Google Scholar]
- [17].Kundanati L et al. , “Fabrication and mechanical characterization of hydrogel infused network silk scaffolds,” Int J Mol Sci, vol. 17, no. 10, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Reed S and Wu BM, “Biological and mechanical characterization of chitosan-alginate scaffolds for growth factor delivery and chondrogenesis,” J Biomed Mater Res B Appl Biomater, vol. 105, no. 2, pp. 272–282, 2017. [DOI] [PubMed] [Google Scholar]
- [19].Wang YF et al. , “Systematic characterization of porosity and mass transport and mechanical properties of porous polyurethane scaffolds,” J Mech Behav Biomed Mater, vol. 65, pp. 657–664, 2017. [DOI] [PubMed] [Google Scholar]
- [20].Askari E et al. , “Micro-CT based finite element modelling and experimental characterization of the compressive mechanical properties of 3-D zirconia scaffolds for bone tissue engineering,” J Mech Behav Biomed Mater, vol. 102, p. 103516, 2020. [DOI] [PubMed] [Google Scholar]
- [21].Tiryaki VM et al. , “AFM feature definition for neural cells on nanofibrillar tissue scaffolds,” Scanning, vol. 34, no. 5, pp. 316–24, 2012. [DOI] [PubMed] [Google Scholar]
- [22].Luque T et al. , “Local micromechanical properties of decellularized lung scaffolds measured with atomic force microscopy,” Acta Biomater, vol. 9, no. 6, pp. 6852–9, 2013. [DOI] [PubMed] [Google Scholar]
- [23].Lee HU et al. , “Preparation and atomic force microscopy (AFM) characterization of DNA scaffolds as a template for protein immobilization,” J Nanosci Nanotechnol, vol. 14, no. 11, pp. 8699–702, 2014. [DOI] [PubMed] [Google Scholar]
- [24].Liang H et al. , “Exploring the complex mechanical properties of xanthan scaffolds by AFM-based force spectroscopy,” Beilstein J Nanotechnol, vol. 5, pp. 365–373, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wingender B et al. , “Hierarchical characterization and nanomechanical assessment of biomimetic scaffolds mimicking lamellar bone via atomic force microscopy cantilever-based nanoindentation,” Materials (Basel), vol. 11, no. 7, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Li M et al. , “Tunable hybrid biopolymeric hydrogel scaffolds based on atomic force microscopy characterizations for tissue engineering,” IEEE Trans Nanobioscience, vol. 18, no. 4, pp. 597–610, 2019. [DOI] [PubMed] [Google Scholar]
- [27].Iturri J and Toca-Herrera JL, “Characterization of Cell Scaffolds by Atomic Force Microscopy,” Polymers (Basel), vol. 9, no. 8, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Carone TW and Hasenwinkel JM, “Mechanical and morphological characterization of homogeneous and bilayered poly(2-hydroxyethyl methacrylate) scaffolds for use in CNS nerve regeneration,” J Biomed Mater Res B Appl Biomater, vol. 78, no. 2, pp. 274–82, 2006. [DOI] [PubMed] [Google Scholar]
- [29].Shojaei S et al. , “Essential functionality of endometrial and adipose stem cells in normal and mechanically motivated conditions,” J Biomater Tiss Eng, vol. 3, no. 5, pp. 581–588, 2013. [Google Scholar]
- [30].Rubiano A et al. , “Mechanical characterization by mesoscale indentation: advantages and pitfalls for tissue and scaffolds,” Tissue Eng Part C Methods, vol. 25, no. 10, pp. 619–629, 2019. [DOI] [PubMed] [Google Scholar]
- [31].Shinato KW et al. , “Principle and application of atomic force microscopy (AFM) for nanoscale investigation of metal corrosion,” Corros Rev, vol. 38, no. 5, pp. 423–432, 2020. [Google Scholar]
- [32].Sokolov I, Chapter 1: Atomic Force Microscopy in Cancer Cell Research, Cancer Nanotechnology. American Scientific Publishers, 2006. [Google Scholar]
- [33].Lamarque JL et al. , “Acoustic microscopy: a new tool for ultrasonic breast tissue characterization,” Eur J Radiol, vol. 3, no. 3, p. 221, 1983. [PubMed] [Google Scholar]
- [34].Aryan P et al. , “An Overview of Non-Destructive Testing Methods for Integrated Circuit Packaging Inspection,” Sensors (Basel), vol. 18, no. 7, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Yu H, “Scanning acoustic microscopy for material evaluation,” Appl Microsc, vol. 50, no. 1, p. 25, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Mohamed ETA and Declercq NF, “Giga-Hertz ultrasonic microscopy: Getting over the obscurity- A short review on the biomedical applications,” Physics in Medicine, vol. 9, p. 100025, 2020. [Google Scholar]
- [37].Khramtsova E et al. , “Impulse acoustic microscopy: A new approach for investigation of polymer and natural scaffolds,” Polym Eng Sci, vol. 57, no. 7, pp. 709–715, 2017. [Google Scholar]
- [38].Song PF et al. , “Comb-push ultrasound shear elastography (CUSE): a novel method for two-dimensional shear elasticity imaging of soft tissues,” Ieee T Med Imaging, vol. 31, no. 9, pp. 1821–1832, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Urban MW et al. , “A review of shearwave dispersion ultrasound vibrometry (SDUV) and its spplications,” Curr Med Imaging Rev, vol. 8, no. 1, pp. 27–36, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Han ZL et al. , “Optical coherence elastography assessment of corneal viscoelasticity with a modified Rayleigh-Lamb wave model,” J Mech Behav Biomed, vol. 66, pp. 87–94, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Liu HC et al. , “Four-dimensional (4D) phase velocity optical coherence elastography in heterogeneous materials and biological tissue,” Biomed Opt Express, vol. 11, no. 7, pp. 3795–3817, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Liu HC et al. , “Fluid surface tension evaluation using capillary wave measurement with optical coherence tomography,” Aip Adv, vol. 10, no. 5, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Gaihre B et al. , “Spatial and uniform deposition of cell-laden constructs on 3D printed composite phosphorylated hydrogels for improved osteoblast responses,” J Mater Sci, vol. 56, no. 31, pp. 17768–17784, 2021. [Google Scholar]
- [44].Gaihre B et al. , “Bifunctional hydrogel for potential vascularized bone tissue regeneration,” Mater Sci Eng C Mater Biol Appl, vol. 124, p. 112075, 2021. [DOI] [PubMed] [Google Scholar]
- [45].Dadsetan M et al. , “Characterization of photo-cross-linked oligo[poly(ethylene glycol) fumarate] hydrogels for cartilage tissue engineering,” Biomacromolecules, vol. 8, no. 5, pp. 1702–1709, 2007. [DOI] [PubMed] [Google Scholar]
- [46].Jo S et al. , “Synthesis and characterization of oligo(poly(ethylene glycol) fumarate) macromer,” Macromolecules, vol. 34, no. 9, pp. 2839–2844, 2001. [Google Scholar]
- [47].Zhu J et al. , “Coaxial excitation longitudinal shear wave measurement for quantitative elasticity assessment using phase-resolved optical coherence elastography,” Opt Lett, vol. 43, no. 10, pp. 2388–2391, 2018. [DOI] [PubMed] [Google Scholar]
- [48].Catheline S and Benech N, “Longitudinal shear wave and transverse dilatational wave in solids,” J Acoust Soc Am, vol. 137, no. 2, pp. EL200–5, 2015. [DOI] [PubMed] [Google Scholar]
- [49].Urban MW, “Production of acoustic radiation force using ultrasound: methods and applications,” Expert Rev Med Devices, vol. 15, no. 11, pp. 819–834, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Kirby MA et al. , “Optical coherence elastography in ophthalmology,” J Biomed Opt, vol. 22, no. 12, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Shung KK, “Diagnostic ultrasound : imaging and blood flow measurements,” 2015.
- [52].Liu HC et al. , “Two-dimensional (2D) dynamic vibration optical coherence elastography (DV-OCE) for evaluating mechanical properties: a potential application in tissue engineering,” Biomed Opt Express, vol. 12, no. 3, pp. 1217–1235, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Kasai C et al. , “Real-time two-dimensional blood-flow imaging using an auto-correlation technique,” Ieee T Son Ultrason, vol. 32, no. 3, pp. 458–464, 1985. [Google Scholar]
- [54].Zhu J et al. , “Coaxial excitation longitudinal shear wave measurement for quantitative elasticity assessment using phase-resolved optical coherence elastography,” Opt Lett, vol. 43, no. 10, pp. 2388–2391, 2018. [DOI] [PubMed] [Google Scholar]
- [55].Tearney GJ et al. , “Determination of the refractive-index of highly scattering human tissue by optical coherence tomography,” Opt Lett, vol. 20, no. 21, pp. 2258–2260, 1995. [DOI] [PubMed] [Google Scholar]
- [56].Calixto S et al. , “Gelatin as a photosensitive material,” Molecules, vol. 23, no. 8, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Liu HC et al. , “Acoustic radiation force optical coherence elastography for evaluating mechanical properties of soft condensed matters and its biological applications,” J Biophotonics, p. e201960134, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Liu HC et al. , “Optical coherence tomography for evaluating capillary waves in blood and plasma,” Biomed Opt Express, vol. 11, no. 2, pp. 1092–1106, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Zhang X and Greenleaf JF, “Estimation of tissue’s elasticity with surface wave speed,” J Acoust Soc Am, vol. 122, no. 5, pp. 2522–5, 2007. [DOI] [PubMed] [Google Scholar]
- [60].Liu HC and Urban MW, “Optical coherence viscometry,” Appl Phys Lett, vol. 118, no. 16, p. 164102, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Liu HC et al. , “Characterizing blood clots using acoustic radiation force optical coherence elastography and ultrasound shear wave elastography,” Phys Med Biol, vol. 66, no. 3, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Liu HC et al. , “Acoustic radiation force optical coherence elastography for evaluating mechanical properties of soft condensed matters and its biological applications,” J Biophotonics, vol. 13, no. 3, p. e201960134, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Rouyer J et al. , “Tissue characterization using simultaneous estimation of backscatter coefficient and elastic shear modulus,” in 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 16–20 Aug. 2016 2016, pp. 2881–2884. [DOI] [PubMed] [Google Scholar]
- [64].Bailey M et al. , “Viscoelastic properties of biopolymer hydrogels determined by Brillouin spectroscopy: A probe of tissue micromechanics,” Sci Adv, vol. 6, no. 44, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Edrei E and Scarcelli G, “Brillouin micro-spectroscopy through aberrations via sensorless adaptive optics,” Appl Phys Lett, vol. 112, no. 16, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Shao P et al. , “Etalon filters for Brillouin microscopy of highly scattering tissues,” Opt Express, vol. 24, no. 19, pp. 22232–22238, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Viljoen A et al. , “Force spectroscopy of single cells using atomic force microscopy,” Nature Reviews Methods Primers, vol. 1, no. 1, p. 63, 2021. [Google Scholar]
- [68].Zhang YW et al. , “Hydrogel: a potential therapeutic material for bone tissue engineering,” Aip Adv, vol. 11, no. 1, 2021. [Google Scholar]
- [69].Qin X et al. , “Matrix stiffness modulates ILK-mediated YAP activation to control the drug resistance of breast cancer cells,” Biochim Biophys Acta Mol Basis Dis, vol. 1866, no. 3, p. 165625, 2020. [DOI] [PubMed] [Google Scholar]
- [70].Pfeifer CR et al. , “Genome variation across cancers scales with tissue stiffness - an invasion-mutation mechanism and implications for immune cell infiltration,” Curr Opin Syst Biol, vol. 2, pp. 103–114, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


