Abstract
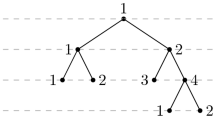
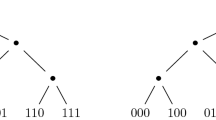
Let T n be the complete binary tree of height n considered as the Hasse-diagram of a poset with its root 1 n as the maximum element. For a rooted tree T, define two functions counting the embeddings of T into T n as follows A(n;T)=|{S \( \subseteq \) T n : 1 n ∈S, S≅T}|, and B(n;T)=|{S \( \subseteq \) T n :1 n ∉S, S≅T}|. In this paper we investigate the asymptotic behavior of the ratio A(n;T)/B(n;T), and we show that lim n→∞[A(n;T)/B(n;T)]=2ℓ;−1−1, for any tree T with ℓ leaves.
Similar content being viewed by others
References
Halmos, P. R.: Measure Theory, Springer, New York, 1974.
Kubicki, G., Lehel, J. and Morayne, M.: A ratio inequality for binary trees and the best secretary, Combin. Probab. Comput. 11 (2002), 149–161.
Kubicki, G., Lehel, J. and Morayne, M.: Counting chains and antichains in the complete binary tree, Unpublished.
Morayne, M.: Partial order analogue of the secretary problem; the binary tree case, Discrete Math. 184 (1998), 165–181.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kubicki, G., Lehel, J. & Morayne, M. An Asymptotic Ratio in the Complete Binary Tree. Order 20, 91–97 (2003). https://doi.org/10.1023/B:ORDE.0000009243.79750.85
Issue Date:
DOI: https://doi.org/10.1023/B:ORDE.0000009243.79750.85