Abstract
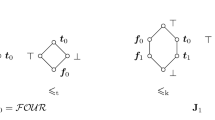
The past few decades have seen a resurgence ofreasoning techniques in artificial intelligenceinvolving both classical and non-classical logics. Inhis paper, ``Multi-valued Logics: A Uniform Approach toReasoning in Artificial Intelligence'', Ginsberg hasshown that through the use of bilattices,several reasoning techniques can be unified under asingle framework. A bilattice is a structure that canbe viewed as a class of truth values that canaccommodate incomplete and inconsistent informationand in certain cases default information. Inbilattice theory, knowledge is ordered along twodimensions: truth/falsity and certainty/uncertainty. By defining the corresponding bilattices as truthspaces, Ginsberg has shown that the same theoremprover can be used to simulate reasoning in firstorder logic, default logic, prioritized default logicand assumption truth maintenance system. Although thisis a significant contribution, Ginsberg's paper waslengthy and involved. This paper summarizes some ofthe essential concepts and foundations of bilatticetheory. Furthermore, it discusses the connections ofbilattice theory and several other existingmulti-valued logics such as the various three-valuedlogics and Belnap's four-valued logic. It is notedthat the set of four truth values in Belnap's logicform a lattice structure that is isomorphic to thesimplest bilattice. Subsequently, Fitting proposed aconflation operation that can be used to selectsub-sets of truth values from this and otherbilattices. This method of selecting sub-sets oftruth values provides a means for identifyingsub-logic in a bilattice.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Anderson, A. R. & Belnap Jr, N. D. (1975). Entailment: The Logic of Relevance and Necessity 1. Princeton University Press.
Belnap Jr, N. D. (1975). A Useful Four-Valued Logic. In Dunn and Epstein (eds.) Modern Uses of Multiple-valued Logic, 8–41. D. Reidel Publishing Company.
Belnap Jr, N. D. & Steel Jr, T. B. (1976). Erotetic Logic: An Introduction to the Logic of Questions and Answers. Yale University Press.
Bochvar, D. (1939). On Three-Valued Logical Calculus and Its Applications to the Analysis of Contradictions. Matematiceskij Sbornik 4: 353–369.
de Kleer, J. (1986). An Assumption-Based Truth Maintenance System. Artificial Intelligence 28: 127–162.
Doyle, J. (1979). A Truth Maintenance System. Artificial Intelligence 12: 231–272.
Etherington, D. W. (1988). Reasoning with Incomplete Information. Research Notes in Artificial Intelligence. Morgan Kaufman.
Fitting, M. (1989). Fitting. Bilattices and the Theory of Truth. Journal of Philosophical Logic 18: 225–256.
Fitting, M. (1991). Bilattices and the Semantics of Logic Programming. Journal of Logic Programming (August) 11(2): 91–116.
Fitting, M. (1993). The Family of Stable Models. Journal of Logic Programming (Preprint).
Ginsberg, M. (1987). Readings in Non-Monotonic Reasoning. Morgan Kaufmann: Los Alto, CA.
Ginsberg, M. (1988). Multivalued logics: A Uniform Approach to Reasoning in Artificial Intelligence. Computational intelligence 4: 265–316.
Kleene, S. (1952). Introduction of Metamathematics. Van Nostrand.
Lukasiewicz, J. (1920). On 3-Valued Logic. In McCall, S. (ed.) Polish Logic. Oxford University Press.
McCarthy, J. (1980). Circumscription-a Form of Non-Monotonic Reasoning. Artificial Intelligence 13: 27–39.
McCarthy, J. (1986). Applications of Circumscription to Formalizing Common Sense Knowledge. Artificial Intelligence 28: 89–118.
Moore, R. (1985). Semantic Considerations on Non-Monotonic Logic. Artificial Intelligence 25: 75–94.
Reiter, R. (1987). Non-Monotonic Reasoning. Annual Review of Computer Science 2: 147–186 (Annual Reviews, Palo Alto, CA).
Reiter, R. (1990). A Logic for Default Reasoning. Artificial Intelligence 13: 81–132.
Sandewall, E. (1985). A Functional Approach to Non-monotonic Logic. In Proceedings of the Ninth International Joint Conference on Artificial Intelligence, 100–106.
Scott, D. (1970). Outline of a Mathematical Theory of Computation. In Proceeding of the Fourth Annual Princeton Conference on Information Sciences and Systems, 167–176.
Scott, D. (1972). Continuous Lattices. In Toposes, Algebraic Geometry and Logic. Lecture Notes in Mathematic, 274, 97–136. Springer-verlag.
Scott, D. (1973). Models for Various Type-free Calculi. Logic, Methodology and Philosophy of Science IV. In Suppes, Henkin, Juja, Moisil (eds.) Proceedings of the Fourth International Congress for Logic. Methodology and the Philosophy of Science, Bucharest, 1971.
Sim, K. M. (1994). Beliefs and Bilattices. In Proceedings of the Eighth International Symposium on Methodologies for Intelligent Systems, Charlotte, North Carolina. Lecture Notes in Artificial Intelligence, 869, 594–603. Springer Verlag.
Sim, K. M. (1995). A Multi-Valued Epistemic Logic. Ph.D. Dissertation, Department of Computer Science, University of Calgary, Calgary, AB, Canada.
Turner, R. (1984). Logics for Artificial Intelligence. Ellis Horwood Series Artificial Intelligence, Ellis Horwood Limited.
Zadeh, L. (1979). A Theory of Approximate Reasoning. In J. Hayes, Michie, D. and Mikulich, L.I. (eds.) Machine Intelligence 9, 149–194. Halstead Press: New York.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Sim, K.M. Bilattices and Reasoning in Artificial Intelligence: Concepts and Foundations. Artificial Intelligence Review 15, 219–240 (2001). https://doi.org/10.1023/A:1011049617655
Issue Date:
DOI: https://doi.org/10.1023/A:1011049617655