Abstract
COVID-19 has taught us that a pandemic can significantly increase biometric risk and at the same time trigger crashes of the stock market. Taking these potential co-movements of financial and non-financial risks into account, we study the portfolio problem of an agent who is aware that a future pandemic can affect her health and personal finances. The corresponding stochastic dynamic optimization problem is complex: It is characterized by a system of Hamilton-Jacobi-Bellman equations which are coupled with optimality conditions that are only given implicitly. We prove that the agent’s value function and optimal policies are determined by the unique global solution to a system of non-linear ordinary differential equations. We show that the optimal portfolio strategy is significantly affected by the mere threat of a potential pandemic.
Keywords: Dynamic programming, Existence and uniqueness, Verification theorem, Portfolio theory, Recursive utility
1. Introduction
COVID-19 has shown that a pandemic can significantly increase biometric risk and at the same time trigger crashes of the stock market. Consequently, the threat of (future) pandemics should have a significant effect on financial decisions including the consumption-portfolio choice of a household. Taking this threat into account, the consumption-portfolio problem of an agent becomes a complex stochastic control problem. To capture the different states of the economy (normal vs. pandemic) and the health of the agent, our model involves a continuous-time Markov chain. The stock dynamics are modeled by a jump-diffusion process with state-dependent coefficients. We allow for a stock market crash when there is a transition into the pandemic state. Apart from these financial aspects, there are also effects on the personal situation of the agent: During the pandemic, she can be infected by the pandemic disease and recover or die. In other words, financial risk and health/mortality risk are intertwined, which distinguishes a pandemic from other crises.
We thus have to solve a dynamic stochastic control problem that contains a continuous-time Markov chain, different types of jump processes, as well as regime-dependent financial and non-financial parameters. The particular link between financial and health risks in the context of portfolio choice is new and leads to an involved dynamic optimization problem where the first-order conditions are mathematically challenging compared to pure regime-switching frameworks. Likewise, proving existence and uniqueness of the relevant solutions must follow a non-standard routine. First, we prove a verification theorem and show that the solution to the problem is characterized by a system of Hamilton-Jacobi-Bellman (HJB) equations. This system is coupled with optimality conditions, which complicates the analysis. Second, we show that there exists a unique solution to this coupled system. It is given by the unique solution to a system of non-linear ordinary differential equations. Another contribution of our paper is that we analyze our dynamic portfolio problem also for recursive utility in the sense of Duffie & Epstein (1992), which is a generalization of continuous-time-additive utility.
Our numerical results show that pandemics have a sizable effect on the portfolio and consumption strategy of an agent. In general, the mere threat of a pandemic significantly reduces her stock investment outside of a pandemic (normal times). The possibility of a pandemic crash links the portfolio decision to the optimal consumption policy so that a potential reduction of consumption during a pandemic amplifies the reduction of the stock investment when there is no pandemic. More precisely, we show that a higher probability of a pandemic significantly reduces the stock share in normal times. Furthermore, higher additional costs during a pandemic also lead to a reduction of the stock share outside of a pandemic. Finally, the expected duration of a pandemic reduces the stock share during a pandemic, whereas the effect is moderate in normal times. Since we also consider recursive utility, we can disentangle the effects of risk aversion and elasticity of substitution (EIS) on the agent’s decision. We find that her risk aversion affects both portfolio and consumption decisions, whereas the EIS mainly affects her consumption decision.
Our paper contributes to a strand of the literature that studies an individual’s consumption-portfolio decision which is formulated as a continuous optimization problem. Continuous-time portfolio theory was established by Merton, 1969, Merton, 1971. Kolm, Tütüncü, & Fabozzi (2014) provide a comprehensive survey over discrete-time portfolio theory.1 There are extensions in multiple directions: Korn & Kraft (2001) study a dynamic portfolio problem with stochastic interest rates. Liu, Longstaff, & Pan (2003) consider such a problem with event risk that does not contain a Markov chain. Ang & Bekaert (2002) and Guidolin & Timmermann (2008) study international portfolio choice with a regime-switching model in discrete-time settings. Honda (2003) considers a portfolio problem with unobservable state. Sass & Haussmann (2004) and Bäuerle & Rieder (2007) study portfolio problems with a hidden Markov chain. Ait-Sahalia, Cacho-Diaz, & Hurd (2009) derive an explicit solution to a problem with jumps. Ait-Sahalia & Hurd (2016) study a consumption-portfolio problem in a class of multidimensional jump-diffusion models in which asset prices are subject to mutually exciting jump processes. Closely related are papers studying regime-switching models such as Sotomayor & Cadenillas (2009), Fu, Wei, & Yang (2014), and Liu & Chen (2018). Sotomayor & Cadenillas (2009) analyze a portfolio problem for a regime-switching model without jumps and derive a verification theorem in this setting. Fu et al. (2014) consider a regime-switching model without jumps and add derivatives to their framework. Liu & Chen (2018) study a dynamic portfolio problem and regime switching with time-consistent risk measures. All these papers do not contain a framework as in our paper where the first-order conditions and HJB equations are coupled. Bäuerle & Rieder (2009) analyze a financial market with jumps only. Furthermore, there are papers that focus on applications in credit risk such as Kraft & Steffensen (2009). In these models, however, the Markov chains are typically directed, since the number of entities is shrinking over time. This is not the case in our framework. Finally, none of the above papers studies agents with recursive utility.
Notice that our paper uses a primal approach. Recently, there have also been several papers using dual approaches. For instance, Bick, Kraft, & Munk (2013) introduce a method delivering explicit close-to-optimal solutions in incomplete markets. This approach is generalized by Kamma & Pelsser (2021). Chen & Vellekoop (2017) use a duality approach to study a portfolio problem where terminal wealth is allowed to be negative. By contrast, Kraft & Steffensen (2013) analyze portfolio problems with additional constraints.
The remainder of our paper is structured as follows: Section 2 introduces the model setup. Section 3 describes the agent’s stochastic control problem. Section 4 derives the system of HJB equations and the optimality conditions. Section 5 provides economic intuition behind our results. In Section 6, we prove a verification theorem for our setup and show that a unique solution to the system of HJB equations exists. This solution determines the optimal controls of the problem. Section 7 extends our results to continuous-time recursive utility in the sense of Duffie & Epstein (1992). Section 8 provides a detailed calibration of our model. Section 9 reports numerical results. Section 10 concludes. An online appendix contains additional material.
2. Model
We study the consumption-portfolio problem of an investor (agent) who faces the risk that a pandemic starts to spread. To capture this, we introduce a four-state Markov chain with state space . Here means that there is currently no pandemic and means that there is one. The probabilities of switching back and forth between these two states are modeled by the state-dependent transition intensity where is the intensity for jumping from state 0 to state 1, i.e., for being hit by a pandemic. On the other hand, is the intensity for jumping back to the non-pandemic state. This could for instance happen if a vaccine has been developed and herd immunity is reached.
Regardless of whether there is currently a pandemic, the agent can die from an ordinary cause. The corresponding intensity is denoted by , which is assumed to be a continuous function of time .2 Notice that time can be interpreted as the age of the investor, i.e., time-dependent is equivalent to age-dependent. If she dies from an ordinary cause, then the Markov chain jumps to state 2. During a pandemic there is also some excess mortality to die from the pandemic disease. If this happens, then the Markov chain jumps from state 1 to state 3. The corresponding intensity is denoted by and is assumed to be a continuous function of time. To summarize, state 0 and 1 characterize the pandemic situation, whereas state 2 and 3 identify the investor’s cause of death. Formally, state 0 and 1 are transient, whereas state 2 and 3 are absorbing.
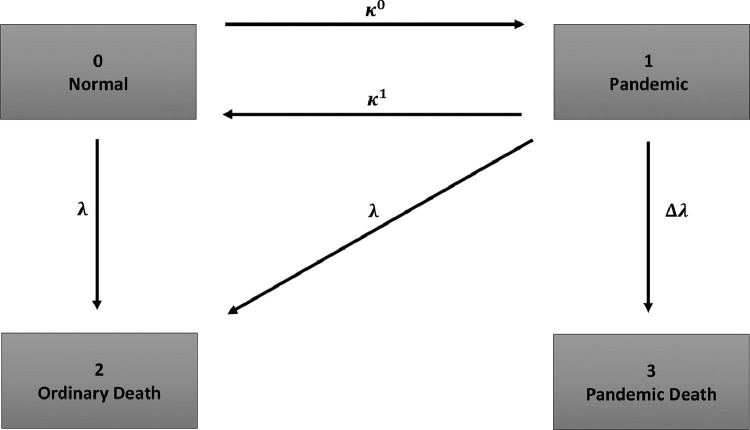
Motivated by the experience during COVID-19, pandemics do not only affect the mortality risk of the agent, but also have an impact on the financial market. Therefore, the asset dynamics can depend on the pandemic situation, i.e., on whether the Markov chain is in state 0 or 1. Notice that our model ends with the death of the investor. Therefore, we do not specify dynamics for state 2 or 3. Fig. 1 depicts the Markov chain that characterizes our setup.3
Fig. 1.
Markov Chain. This figure depicts the Markov chain that characterizes the relevant states. In state 0, there is no pandemic. In state 1, the economy is in a pandemic. State 2 and 3 are absorbing states. State 2 is reached if the agent dies from an ordinary cause, whereas state 2 is reached if the agent dies from the pandemic disease.
The agent can invest in a Treasury bond with constant interest and a stock index (short: stock) that is exposed to pandemic risk.4 For , the asset dynamics are5
| (2.1) |
where is the state-dependent drift and is the state-dependent volatility of the stock index, . However, the drift and the volatility are constant over time in each state. The stock dynamics involve a Brownian motion and point processes , , and . The meaning of the point processes is as follows: models a stock market crash in state . This happens with intensity and the relative jump size is . models a stock market recovery in state . This happens with intensity and the relative jump size is . Conditioning on being in state , both and are Poisson processes. Besides, counts the number of jumps into a pandemic, whereas counts the number of jumps out of a pandemic, i.e.,
where the intensity of is . These jumps also trigger pandemic crashes or recoveries of the stock market and the corresponding jump size is denoted by . A pandemic crash could be an event such as the stock market crash on March 9, 2020. A pandemic recovery can be thought of as a pandemic-induced stock rebound, for instance if stock market participants realize that a majority of the population can be vaccinated and herd immunity will be reached. Therefore, is positive number leading to a loss due to the minus in front of in (2.1), whereas is negative number leading to a gain. Since cannot jump in state 1 and cannot jump in state 0, the stock dynamics (2.1) involve only one of these processes depending on .
Additionally, we assume that the investor can get seriously sick in state 0 or 1. This happens with (state-indpendent) intensity . Such a sickness is costly for the agent (e.g., co-payments) and for simplicity we assume that a fraction of wealth is lost, which is captured by the relative loss .6 In the pandemic state, , it is also possible to be infected by the pandemic disease and survive. This happens with intensity and the relative costs are . During the pandemic, the agent can get infected more than once. By introducing an additional state of the Markov chain, the number of infections could be restricted to be at most one, but it turns out to be less relevant in our numerical examples.
Now, let be be the expected excess return of the stock index and the portfolio strategy (proportion invested in stock). Our model ends at the stopping time defined as
where is the time of death if she dies from the pandemic disease and is the time of death if she dies from an ordinary cause. Formally, and . The constant is a time point where it is extremely unlikely that the agent is still alive and mortality tables typically end, e.g. an age of 120.7 For , the investor’s wealth dynamics thus read
| (2.2) |
where captures additional relative expenses during the pandemic and we set . The meaning of the counting processes is as follows: counts the number of ordinary non-deadly health shocks and counts the number of pandemic non-deadly health shocks. Notice that the intensity of is zero in state 0 and in state 1, i.e., the intensity can be written as for . Furthermore, jumps if the agent dies from an ordinary cause and jumps if the agent dies from the pandemic disease. The intensity of can be written as for .
The investor consumes at a rate of . In our benchmark case, she optimizes time-additive utility of consumption and bequest with respect to the utility function
| (2.3) |
where is her risk-aversion coefficient.8 Her time preferences are captured by the time-preference rate . For some strategy and , we can thus define the corresponding utility index by
where and is her weight of bequest. We assume
| (2.4) |
In Section 8, we calibrate our model. Table 1 summarizes the corresponding parameters.
Table 1.
Benchmark Calibration. This table reports the benchmark calibration of our model. We consider a female agent who is initially 60 years old.
| Symbol | Meaning | Value |
|---|---|---|
| Interest rate | 0.005 | |
| Equity premium in normal state | 0.073 | |
| Equity premium in pandemic state | 0.150 | |
| Volatility in normal state | 0.149 | |
| Volatility in pandemic state | 0.266 | |
| Intensity for crash in normal state | 60/94 | |
| Intensity for crash in pandemic state | 2.44 | |
| Crash size in normal state | 0.067 | |
| Crash size in pandemic state | 0.108 | |
| Intensity for recovery in normal state | 53/94 | |
| Intensity for recovery in pandemic state | 2.44 | |
| Recovery size in normal state | 0.071 | |
| Recovery size in pandemic state | 0.088 | |
| Intensity for transition into pandemic state | 0.13 | |
| Intensity for transition into normal state | 0.4 | |
| Jump size (loss) upon transition into pandemic state | 0.079 | |
| Jump size (gain) upon transition into normal state | -0.080 | |
| Mortality intensity: US social security administration | ||
| Rel. excess mortality intensity during COVID-19 | 0.15 | |
| Intensity of health shock | 0.02 | |
| Relative cost of health shock | 0.02 | |
| Intensity of non-deadly health shock in pandemic state | 0.05 | |
| Relative cost of non-deadly health shock in pandemic state | 0.02 | |
| Excess relative expenses in pandemic state | 0.03 | |
| Risk aversion | 5 | |
| Time preference rate | 0.05 | |
| Bequest weight | 1 |
3. Optimization problem of the agent
As usual, we focus on strategies that are said to be admissible. To formalize this idea, let be a probability space where is the canonical filtration that is generated by the Brownian motion , the Markov Chain , and the jump processes introduced in the previous section.9 Then we can define:
Definition 3.1 Admissible Strategy —
An -valued predictable process is admissible if
The set of admissible strategies is denoted by .
Remarks. (a) The integrability conditions make sure that the Brownian and Poissonian integrals are true martingales, since the integrands are - or -integrable, respectively. This excludes true local martingales and thus policies that are clearly inferior to an optimal strategy.
(b) A portfolio strategy is a stochastic process that can depend on time , wealth , and the state of the economy . If the economy is in a particular state , it is sometimes convenient to denote the policy for that state by . From this perspective, the optimal of our problem is characterized by the policies and in state 0 and 1.
We will show below that the optimal strategy satisfies all these requirements. Notice that conditions (i) and (ii) are reasonable and weak requirements: Condition (i) makes sure that the wealth equation is well-defined. Condition (ii) excludes strategies with extremely negative utility that cannot be optimal anyway. We now define the maximum size of the potential crashes and recoveries:
| (3.1) |
The following proposition shows that all strategies which do not lead to poor outcomes if a jump occurs and which involve consumption rates being at most linear in wealth are admissible.
Proposition 3.2 Tame Strategies Are Admissible —
Letbe an-valued predictable process satisfying the following conditions:
- (i)
For state 0, there exist a lower boundand an upper boundsuch that.
- (ii)
For state 1, there exist a lower boundand an upper boundsuch that.
- (iii)
Consumption is at most linear in wealth, i.e., there is a constantsuch that.
Thenis admissible. We refer to admissible strategies satisfying (i)-(iii) as tame. Analogously, the portfolio strategyof an admissible policyis called tame if it satisfies (i) and (ii).
Remark. Conditions (i) and (ii) are weak requirements. Notice that empirically jump sizes for the S&P500 are less then 20%. For such a calibration, condition (ii) implies that the portfolio strategy must be between and . Strategies with more leverage that do not satisfy this condition are extremely unrealistic.
Proof of Proposition 3.2..
Conditions (i) and (ii) guarantee that the SDE (2.2) has a unique solution with . Therefore, we also get (b) of Definition 3.1. Since as well and all terms involving in the integrability conditions of (c) in Definition 3.1 are bounded, we obtain (c) and thus admissibility of . □
We now define the value function of our consumption-portfolio problem:
| (3.2) |
for the initial values and , .
4. Hamilton-Jacobi-Bellman equations
As we will formally show in Section 6, the solution of the problem can be determined by studying two-coupled HJB equations for state 0 and 1 that are given by
| (4.1) |
| (4.2) |
where is the aggregated intensity to die from an ordinary case or due to the pandemic(“ord. or pan. death”). For both HJB equations, the terminal condition is
| (4.3) |
In both states, optimal consumption reads , . We conjecture
| (4.4) |
and obtain
| (4.5) |
The HJB equations simplify to
| (4.6) |
| (4.7) |
with terminal conditions , , where
The optimal strategy in state 0 satisfies the first-order condition
| (4.8) |
whereas the optimal strategy in state 1 satisfies the first-order condition
| (4.9) |
5. Economic interpretation of optimal policies
The optimal portfolio strategy in the normal state can be written as11
| (5.1) |
Compared to the classical Merton result, the optimal portfolio strategy has three additional terms. The first additional term captures the positive effect of a stock market recovery. The last two terms are crash terms that start with a ratio: expected jump size, or , divided by diffusive variance scaled by the risk aversion of the agent. Both terms have a negative sign and thus reduce the stock proportion. However, the pandemic crash term also involves the ratio . To understand its effect, consider the first-order conditions for consumption
where is the relative consumption loss upon entering the pandemic state. The ratio thus measures the severeness of this loss. Consequently, the pandemic crash term is the product of an ordinary crash term and an adjustment for this loss:
| (5.2) |
The adjustment term increases in the consumption loss and reduces the optimal stock proportion further compared to ordinary stock crashes. Therefore, pandemic crashes lead to a novel link between consumption and investments that does not exist in frameworks with ordinary crashes only.
Notice that effects of a pandemic-induced stock crash and consumption reduction are not simply additive. To see this, we focus on the last two factors in (5.2) and apply a first-order approximation
The last term, is a cross term showing that there is an interaction between stock crash and consumption reduction.
6. Verification, existence, and uniqueness
This section is concerned with proving two theorems: First, we show that if there is a solution to the HJB Eqs. (4.1) and (4.2), then it is indeed the solution to the consumption-portfolio problem. This result is summarized in Theorem 6.1. Second, we prove that there exists a unique solution to the HJB equations. This is summarized in Theorem 6.2.
6.1. Verification theorem
We start with a verification theorem.
Theorem 6.1 Verification —
Assume that the system of HJB Eqs.(4.1)and(4.2)has a solution of the form(4.4)whereis continuously differentiable,. Then we have:
forand all.
Proof
See Online Appendix B. □
6.2. Existence and uniqueness
The first-order conditions (4.8) and (4.9) can be rewritten as
| (6.1) |
where
Theorem 6.2 Existence and Uniqueness —
The Eqs.(4.6)and(4.7)have a unique-solutionandwhere both functions are bounded away from zero and bounded from above. Furthermore, there is a unique optimal portfolio strategy given by(4.8)and(4.9)which is tame.
Proof of Theorem 6.2
We apply the implicit function theorem to (6.1). Notice that is continuously differentiable on with . Thus
Therefore, there exists a continuously differentiable function solving (6.1) for , i.e.,12
Analogously, is continuously differentiable on with . Therefore, there exists a continuously differentiable function solving (6.1) for , i.e.,
We thus obtain a well-defined continuous control given by and satisfying the first-order conditions, which are also sufficient due to the concavity of the problem. Now, substituting and back into (4.6) and (4.7) yields a system of two ordinary differential equations
(6.2) where and and the right-hand side is defined as
(6.3)
(6.4) Integrating the first equation of (6.2), we obtain
(6.5) since (2.4). Here is a constant minimizing , i.e., . Therefore, is bounded away from zero by . Notice that were the optimal policy if , i.e., if there is no loss upon transition into the pandemic. Analogously, one can show that is bounded away from zero by some constant .
Now, we derive upper bounds. From representation (6.5) and the fact that is the minimizer, it is clear that for the suboptimal we get the following estimates
(6.6) and, similarly, for
(6.7) where
and the other constants are given by ,
Now, setting and adding (6.6) and (6.7), we obtain , which, by Gronwall’s lemma gives
i.e., the solutions for and are uniformly bounded from above. To summarize, our prior estimates show that graph of a solution lies in the rectangle where with . Therefore, our candidate is bounded and tame and thus
, are bounded as well. Besides, the right-hand of the system of ordinary differential Eqs. (6.3) and (6.4) is continuous for all . Additionally, given our previous results about the implicit definitions of and the function of the right-hand side has continuous partial derivatives with respect to and and thus satisfies a local Lipschitz condition. Therefore, there exists a unique solution to (6.2).13
Since the right-hand side of (6.2) is continuous, this solution is . □
7. Recursive utility
We now study an investor whose preferences are captured by continuous-time recursive utility (syn. stochastic differential utility), which was introduced by Duffie & Epstein (1992). In contrast to time-additive utility, recursive utility allows us to disentangle the agent’s risk aversion from her elasticity of intertemporal substitution (EIS). This is important since these concepts capture different phenomena: Risk aversion determines how much an agent invests in risky assets, whereas EIS is decisive for how the agent distributes her consumption over time. The utility index for some strategy and is defined by the recursion
where is the weight on the terminal condition. The aggregator is given by
| (7.1) |
where is the time-preference rate, the relative risk aversion, and the elasticity of intertemporal substitution (EIS).
Notice that implies preferences for early resolution of uncertainty, i.e., the agent prefers to obtain any piece of information rather earlier than later.14 For , one obtains time-additive utility as in the previous sections, which implies neutrality towards the resolution of uncertainty. The value function is defined by
| (7.2) |
Duffie & Epstein (1992) show that the solution to problems with stochastic differential utility is also characterized by a system of coupled HJB equations where the aggregator replaces the term .15 The corresponding HJB equations can be found in Online Appendix C. A similar conjecture as for CRRA utility,
| (7.3) |
leads to the following first-order conditions for consumption
| (7.4) |
Notice that optimal consumption (7.4) is different from the time-additive case (4.5) since the exponent is now (compared to ). Consumption thus depends on the agent’s risk aversion and her EIS. The functions are determined by a system of simplified HJB equations:
| (7.5) |
for the non-pandemic state (state 0) and
| (7.6) |
for the pandemic state (state 1).
The terminal condition (4.3) and the conjecture (7.3) lead to the terminal conditions
Notice that in contrast to consumption, the first-order conditions for the portfolio policy do not change compared to time-additive utility and are again (4.8) and (4.9). Quantitatively, however, the results do change, since and will be different compared to the time-additive case. This is a consequence of the pandemic related jumps and . For ordinary portfolio problems where the stock price follows a jump-diffusion process as in Merton (1971), this is not the case and the strategies are the same for time-additive and recursive utility.
We now prove that the above HJB equations have a unique solution if the EIS is below unity and the risk aversion is above two. For our benchmark choice of , we can thus freely vary the EIS between zero and unity and still be sure that a unique solution exists. Notice that for , values of below are less relevant, since they imply preferences for late resolution of uncertainty. In any case, we have enough degrees of freedom to analyze the effect of the EIS on consumption and portfolio choice in the context of pandemics.
Proposition 7.1 Existence and Uniqueness for Recursive Utility —
Ifand, then the results from Theorem6.2also hold for(7.5)and(7.6).
Proof
Under the conditions of this proposition, we have and . Therefore, all arguments of Theorem 6.2 go through since the non-linear terms are qualitatively of the same form. □
Remark. The case is of minor importance, since this restriction implies preferences for late resolution of uncertainty. See Kraft, Seifried, & Steffensen (2013) for a discussion in a different setting.
8. Calibration
In our benchmark case, we consider an agent with time-additive utility and a risk aversion of . The weight on bequest is .16 We use the mortality table provided by the US social security administration to calculate the mortality intensity of a female agent.17 To estimate the excess mortality of COVID-19, we use US data that is available on the website of the Center for Disease Control Prevention (CDC).18
The average percentage of COVID-19 related deaths compared to all deaths is about 15% for females above 55 years. Since the agent of our benchmark case is female and has an initial age of 60 years, we thus set
To calibrate and , which are the intensities to enter or leave the pandemic state, we use significant historic pandemics since 1950 that had a worldwide impact.19
Apart from HIV and MERS, the average duration of a pandemic is about two to three years. Since is the average waiting time to leave the pandemic state, values between 1/3 and 1/2 seem to be reasonable choices. Parametrizing is more involved, since the frequency of pandemics over time seems to increase. If we take the time span from 1950 to 2019, there are 9 pandemics leading to a value of for . If we focus on the pandemics after the millenium, then there are 5 pandemics leading to a value of . So values in the range of 0.13 to 0.25 for seem to be reasonable.
Our model also involves health expenses for non-deadly sicknesses. To calibrate the non-pandemic related health expenses, we use data from the website of the American Cancer Society.20 For females the risk to get cancer is about 38.7% and the risk of dying is about 18.3%, i.e., 20% of the female population get cancer and survive. Taking into account that our agent is initially 60 years old, we thus choose for the sickness intensity and moderate costs of , i.e., 2% of current wealth if she gets sick.21 To calibrate the parameters of a non-deadly pandemic infection, notice that until the end of March 2021 there have been 30m known cases of COVID-19 in the US,22 which is about 9% of the US population. Since health expenses are heterogeneous across cases, we choose moderate numbers of and . In the future, there might be pandemics with higher infection rates and more severe cases.
We fix a real interest rate of 0.5%, which is close to the average real interest rate of the US.23 To estimate the stock parameters, we use daily return index data from CRSP. More details can be found in Online Appendix D. Table 1 summarizes our benchmark calibration.
9. Numerical results
This section reports numerical results for our benchmark calibration and shows how these results vary with risk aversion and EIS. We also study how the size of pandemic costs as well as the probability and the duration of a pandemic affect the optimal strategies. Furthermore, we provide additional robustness checks.
9.1. Risk aversion and EIS
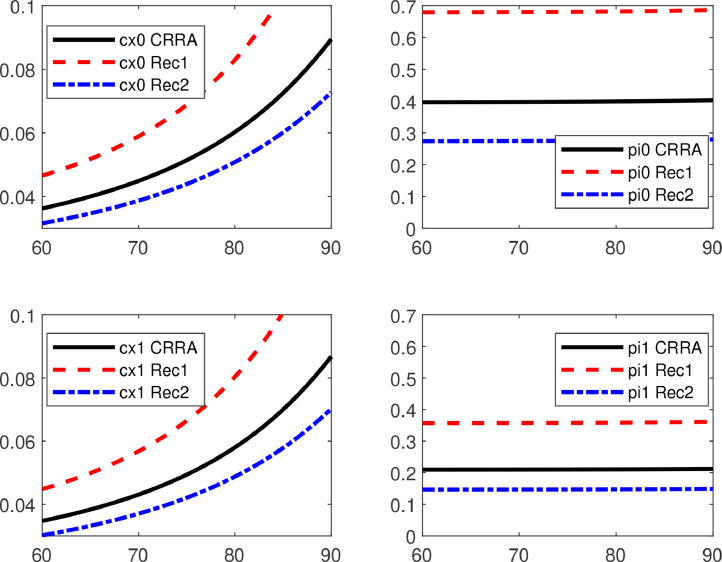
Fig. 2 depicts the optimal consumption-wealth ratios and portfolio policies of a female agent between the age of 60 and 90 years.24
Fig. 2.
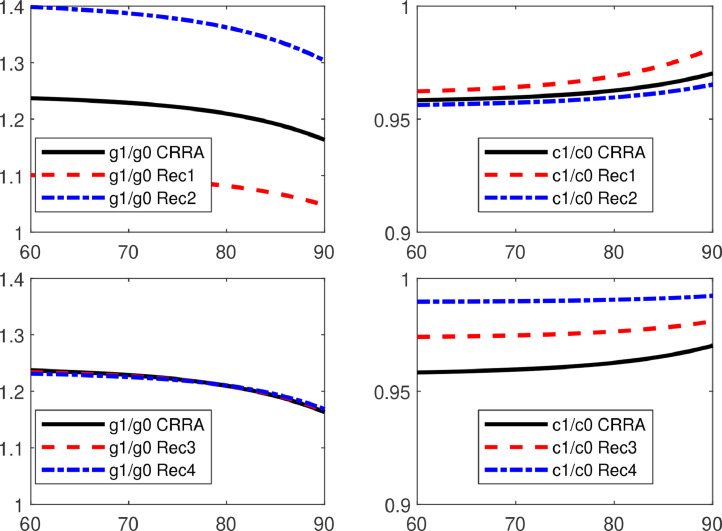
Optimal Policies for Different Risk Aversion. This figure depicts the optimal consumption-wealth ratios (left graphs) and optimal portfolio strategies (right graphs) for different risk aversion. The x-axes show the age of the agent. The two upper graphs depict the results for the normal state. We fix the EIS at and choose risk aversions of . The lower graphs present the corresponding results for the pandemic state. The solid lines are the results for time-additive utility (CRRA) with and . The dashed lines are the results for recursive utility (Rec1) with and . The dashed-dotted lines are the results for recursive utility (Rec2) with and . For the remaining parameters benchmark values are used.
The EIS is fixed at . The two upper graphs show the results in the normal state if we vary the risk aversion. The solid line is our benchmark calibration with time-additive utility (risk aversion of ). The dashed line is for a risk aversion of , whereas the dashed-dotted line is for a risk aversion of . The two lower graphs depict the corresponding results for the pandemic state.
The weight on bequest is calibrated such that the wealth-consumption ratios upon death are unity for both cases.
It can be seen that the portfolio strategies and the consumption-wealth ratios are significantly changing with risk aversion. First, the agent invests less if she is more risk averse, since risk aversion models the agent’s attitude towards risk. Second, she consumes less if she is more risk averse, since higher risk aversion leads to additional precautionary savings.25
Across states the portfolio strategies also change significantly and are much lower in the pandemic state, whereas the change in consumption is less pronounced.
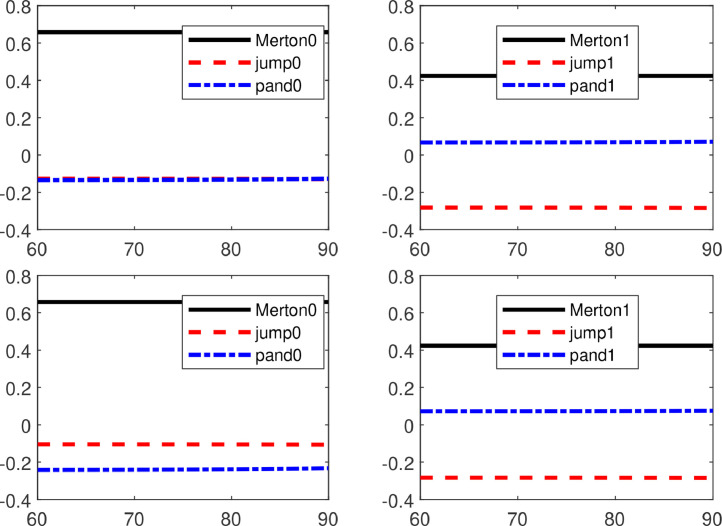
Fig. 3 shows the decomposition of the optimal strategy into the components given in (5.1) if the agent has time-additive utility with . The lines labeled “jump0” and “jump1” depict the net effects of ordinary stock jumps (sum of stock recovery and stock crash). The upper graphs are for (moderate calibration based on the historical pandemics between 1950 and 2019), whereas the lower graphs are for (alternative calibration based on more recent pandemics between 2000 and 2019). For , it can be seen that in the normal state (upper left-hand graph), the contribution of a pandemic crash is similar than the net effect of ordinary stock jumps. If we focus on the pandemics that happened after the year 2000, then the frequency of a pandemic almost doubles ( instead of ). The lower graph on the left-hand side of Fig. 3 shows that in this case the contribution of a pandemic crash to the optimal portfolio policy is much bigger than of ordinary stock jumps. On the other hand, the graphs on the right-hand side show that in the pandemic state, the jump component is very negative, since stock crashes are more likely and larger than in normal times. The pandemic recovery term contributes moderately to the portfolio policy.
Fig. 3.
Decomposition of Portfolio Policies. This figure depicts the optimal portfolio policies decomposed into the Merton term, the sum of the ordinary jump terms (stock crash and stock recovery), and the pandemic term according to (5.1). The x-axes show the age of the agent who has time-additive utility with . The upper graphs show the results if pandemics occur with intensity , whereas in the lower graphs a pandemic occurs with intensity . The left graphs depict the results for normal state, whereas the right graphs for pandemic state. For the remaining parameters benchmark values are used.
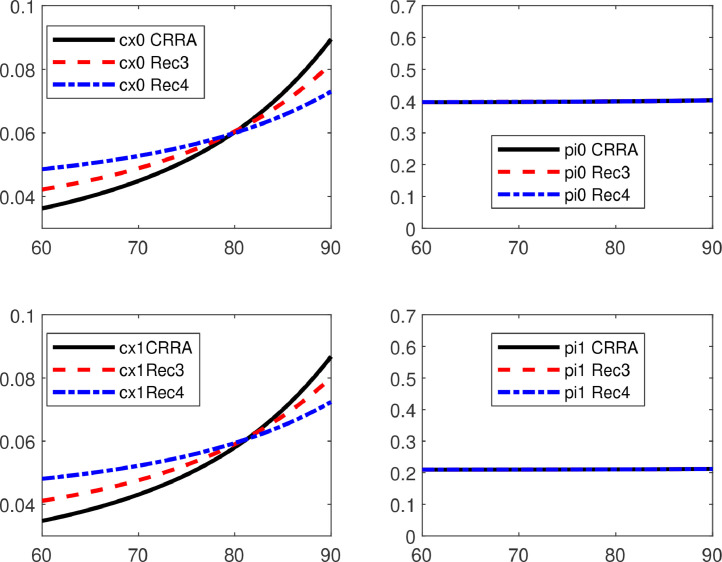
We now turn to the effect of the EIS. Fig. 4 depicts the corresponding results for the optimal consumption-wealth ratios and portfolio policies. The risk aversion is fixed at . The two upper graphs show the results in the normal state if we vary the EIS. The solid lines are our benchmark calibration with time-additive utility (EIS of ). The dashed lines are for an EIS of , whereas the dashed-dotted lines are for an EIS of . The two lower graphs depict the results for the pandemic state. It can be seen that the portfolio strategies are still significantly state dependent (0.4 in the normal state vs. 0.2 in the pandemic state), but hardly age dependent or EIS dependent. However, the effect of the EIS on the level of consumption over time is more pronounced. The consumption-wealth ratios significantly vary with age and EIS.
Fig. 4.
Optimal Policies for Different EIS. This figure depicts the optimal consumption-wealth ratios (left graphs) and optimal portfolio strategies (right graphs) for different EIS. The x-axes show the age of the agent. The two upper graphs depict the results for the normal state. We fix the risk aversion at and choose an EIS of . The lower graphs present the corresponding results for the pandemic state. The solid lines are the results for time-additive utility (CRRA) with and . The dashed lines are the results for recursive utility (Rec3) with and . The dashed-dotted lines are the results for recursive utility (Rec4) with and . For the remaining parameters benchmark values are used.
Formally the different effects of risk aversion and EIS can be understood by considering the functions , , and the ratio . The portfolio strategies contain this ratio, whereas the consumption-wealth ratios are given by (4.5) and (7.4), i.e., they depend on raised to the power of , which depends on the risk aversion and the EIS. The two graphs on the left-hand side of Fig. 5 show that is significantly affected by the risk aversion, but hardly varies with the EIS. Since the EIS enters the portfolio strategy only via , this strategy is hardly affected if the EIS changes.
Fig. 5.
Value Function Ratio vs. Consumption Ratio. This figure depicts the ratio and for different EIS and risk aversion. In all graphs, the solid lines represent the results for time-additive utility (CRRA) where the EIS is and . In the upper graphs, we vary the risk aversion and fix the EIS at . The dashed lines are the results for recursive utility (Rec1) with and . The dashed-dotted lines are the results for recursive utility (Rec2) with and . In the lower graphs, we vary the EIS and fix the risk aversion at . The dashed lines are the results for recursive utility (Rec3) with and . The dashed-dotted lines are the results for recursive utility (Rec4) with and .
On the other hand, the consumption ratio between both states is given by
Therefore, not only the consumption-wealth ratio, but also the consumption ratio between both states varies with the risk aversion and the EIS, as shown by the graphs on the right-hand side of Fig. 5. Apparently, the effect of the EIS is more pronounced than the effect of the risk aversion.
9.2. Robustness checks
First, we provide robustness checks for the expected excess return in the pandemic state. We compare our benchmark calibration with . It turns out that the optimal portfolio policy in the non-pandemic state is hardly affected and varies between 38.6% and 40.4% at the age of 60 years. Not surprisingly, the risky share in the pandemic state is much more affected and is only 12.4% for , but 29.4% for , whereas it is 20.9% in the benchmark case.
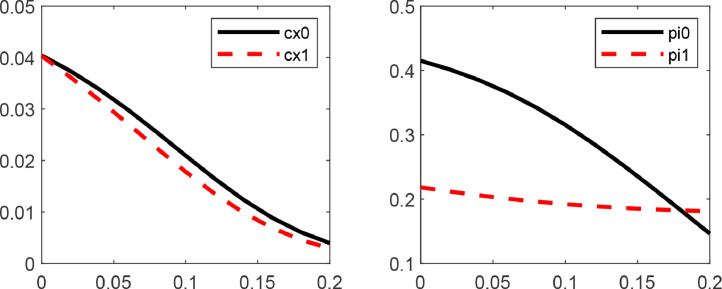
Next, we vary the relative pandemic costs occurring in state 1 captured by . We fix the agent’s age at 60 years. As can be seen from Fig. 6 , the consumption-wealth ratio and the portfolio policy in the non-pandemic state change significantly if pandemic costs increase. The agent cuts down on consumption in normal times and reduces her risky share heavily. Instead, she increases her precautionary savings to be able to cover future costs if a pandemic hits the economy. In turn, the portfolio strategy in the pandemic state is only moderately affected by pandemic costs.
Fig. 6.
Optimal Policies and Pandemic Costs. This figure depicts the optimal consumption-wealth ratios (left graph) and optimal portfolio strategies (right graph) for different values of the additional costs induced by pandemics. The x-axes varies between 0 and 0.2. Solid (dashed) lines show the results for the normal (pandemic) state. The agent has time-additive utility with and an age of 60 years. For the remaining parameters, benchmark values are used.
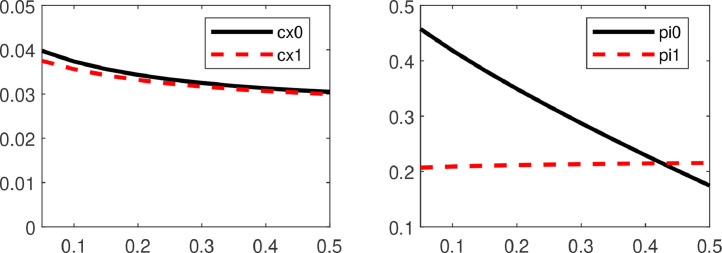
Now, we vary the probability that a pandemic occurs captured by the intensity . Fig. 7 depicts the corresponding consumption-wealth ratios and portfolio strategies if is between 0 and 0.5. In both states, the agent cuts down on consumption if a pandemic becomes more likely. The most significant effect is however on the optimal portfolio strategy in the normal state, which is reduced to less than 20% if a pandemic occurs with intensity .
Fig. 7.
Optimal Policies and Probability of Pandemic. This figure depicts the optimal consumption-wealth ratios (left graph) and optimal portfolio strategies (right graph) for different intensities to enter the pandemic state. The x-axes varies between 0 and 0.5. Solid (dashed) lines show the results for the normal (pandemic) state. The agent has time-additive utility with and an age of 60 years. For the remaining parameters, benchmark values are used.
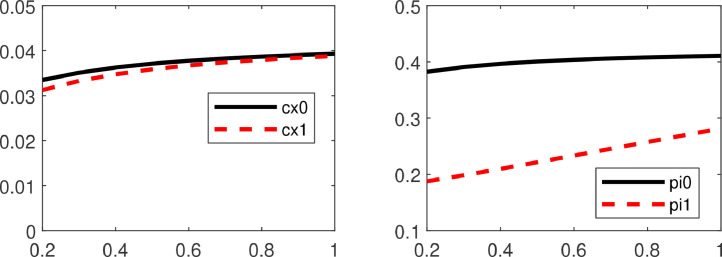
If we change the duration of a pandemic by varying , Fig. 8 shows opposite effects. For high values of , i.e., short durations, the agent increases consumption in both states (left graph). Also the portfolio strategy in the pandemic significantly increases in this case (dashed line in the right graph). This is because pandemics are less damaging if their duration is smaller.
Fig. 8.
Optimal Policies and Duration of Pandemic. This figure depicts the optimal consumption-wealth ratios (left graph) and optimal portfolio strategies (right graph) for different intensities to leave the pandemic state. The x-axes varies between 0.2 and 1.0. Solid (dashed) lines show the results for the normal (pandemic) state. The agent has time-additive utility with and an age of 60 years. For the remaining parameters, benchmark values are used.
Finally, we perform robustness checks by simultaneously varying some of the parameters related to pandemics. For the sake of brevity, we focus on the time-additive case with .26
The first two rows of Table 2 show our results if there are no jumps upon transition between pandemic and non-pandemic state (pure regime-switching model). In this situation, the optimal stock position is about 50% in normal times. This is independent of the expected duration of a pandemic. In the subsequent rows, we allow for pandemic crashes and recoveries. It can be seen that the size of a pandemic crash has a significant effect on the portfolio strategy in the non-pandemic state. The second half of Table 2 below the double line reports results if we use calibrations of the model that go beyond the parameters estimated from the COVID-19 data in Section 8. In particular, we provide optimal policies for extreme expected frequencies and durations of pandemics (captured by and ). It can be seen that the optimal portfolio strategy can even be negative if the pandemic is expected to be very severe. Also the consumption-wealth ratios are significantly affected and vary between 0.027 and 0.042, i.e., in the best-case scenario consumption can be about 55% higher than in the worst-case scenario.
Table 2.
Robustness Checks. For different expected frequencies and durations of pandemics (captured by and ), we vary the sizes of pandemic crashes and recoveries. We report the optimal portfolio strategies as well as the consumption-wealth ratios , , if the agent is currently 60 years old.
| 0.13 | 0.50 | 0.00 | 0.00 | 0.503 | 0.170 | 0.039 | 0.037 |
| 0.00 | 0.33 | 0.00 | 0.00 | 0.503 | 0.170 | 0.037 | 0.035 |
| 0.00 | 0.50 | 0.00 | 0.00 | 0.503 | 0.170 | 0.036 | 0.035 |
| 0.25 | 0.33 | 0.00 | 0.00 | 0.503 | 0.170 | 0.034 | 0.032 |
| 0.13 | 0.50 | 0.08 | -0.08 | 0.399 | 0.222 | 0.037 | 0.036 |
| 0.13 | 0.33 | 0.08 | -0.08 | 0.391 | 0.202 | 0.035 | 0.034 |
| 0.13 | 0.50 | 0.15 | -0.08 | 0.301 | 0.223 | 0.035 | 0.034 |
| 0.13 | 0.33 | 0.15 | -0.08 | 0.289 | 0.203 | 0.034 | 0.033 |
| 0.25 | 0.50 | 0.08 | -0.08 | 0.320 | 0.224 | 0.034 | 0.033 |
| 0.25 | 0.33 | 0.08 | -0.08 | 0.311 | 0.205 | 0.033 | 0.031 |
| 0.25 | 0.50 | 0.15 | -0.08 | 0.169 | 0.226 | 0.033 | 0.032 |
| 0.25 | 0.33 | 0.15 | -0.08 | 0.158 | 0.206 | 0.031 | 0.030 |
| 0.05 | 0.20 | 0.04 | -0.04 | 0.475 | 0.177 | 0.038 | 0.034 |
| 0.05 | 0.20 | 0.04 | 0.00 | 0.475 | 0.170 | 0.038 | 0.034 |
| 0.05 | 1.00 | 0.04 | -0.04 | 0.485 | 0.226 | 0.042 | 0.041 |
| 0.05 | 1.00 | 0.04 | 0.00 | 0.485 | 0.170 | 0.042 | 0.040 |
| 0.05 | 0.20 | 0.20 | -0.04 | 0.340 | 0.178 | 0.036 | 0.032 |
| 0.05 | 0.20 | 0.20 | 0.00 | 0.339 | 0.170 | 0.035 | 0.032 |
| 0.05 | 1.00 | 0.20 | -0.04 | 0.385 | 0.228 | 0.039 | 0.038 |
| 0.05 | 1.00 | 0.20 | 0.00 | 0.382 | 0.170 | 0.039 | 0.038 |
| 0.50 | 0.20 | 0.04 | -0.04 | 0.325 | 0.181 | 0.029 | 0.028 |
| 0.50 | 0.20 | 0.04 | 0.00 | 0.324 | 0.170 | 0.028 | 0.027 |
| 0.50 | 1.00 | 0.04 | -0.04 | 0.340 | 0.230 | 0.034 | 0.034 |
| 0.50 | 1.00 | 0.04 | 0.00 | 0.337 | 0.170 | 0.033 | 0.033 |
| 0.50 | 0.20 | 0.20 | -0.04 | -0.181 | 0.181 | 0.028 | 0.027 |
| 0.50 | 0.20 | 0.20 | 0.00 | -0.184 | 0.170 | 0.028 | 0.027 |
| 0.50 | 1.00 | 0.20 | -0.04 | -0.146 | 0.231 | 0.033 | 0.032 |
| 0.50 | 1.00 | 0.20 | 0.00 | -0.154 | 0.170 | 0.031 | 0.031 |
We have also varied the excess mortality and parameters that are directly related to health expenses (, , , ), but the changes are only moderate. Therefore, the main effects on the optimal decisions of the agent come from the financial impact of the pandemic.
10. Conclusion
This paper has studied the consumption-portfolio problem of an agent who faces the threat of a future pandemic. We show that the mere threat has a significant effect on her portfolio decision when there is no pandemic. In particular, potential expenses during a pandemic trigger precautionary savings that can considerably reduce the size of her stock investment. On the theoretical side, we offer a complete solution to an involved stochastic control problem where the optimality conditions are only given implicitly. We show that the solution is determined by the unique solution to a non-linear system of differential equations. Our framework can be extended to include additional financial or non-financial states.
Acknowledgments
We thank Roman Slowinski (the editor) and three anonymous referees for helpful comments and suggestions. All remaining errors are our own.
Portfolio theory should not be confused with portfolio decision analysis (PDA). See Liesiöa, Salo, Keisler, & Morton (2021) for a recent survey.
We use the following convention: If is a deterministic function of time, then we write , whereas we write if is a stochastic process. However, we sometimes skip the dependencies to keep the notation simple.
To capture additional scenarios, we could add further states to the Markov chain.
We could easily introduce state-dependent interest rates. This is realistic since central banks might want to lower interest rates to mitigate recessions resulting from pandemics.
In the and term of the stock, all can be replaced by , since one can change coefficients on zero sets and the jumps of the point processes constitute a zero set w.r.t. the Lebesgue measure.
For simplicity, we assume that health care costs are constant. If these costs are stochastic as suggested by French & Jones (2004), then and must be replaced by the corresponding certainty equivalents. Details can be found in Online Appendix A.
Notice that an age of 120 it is not necessary equal to , since the model does not necessarily start at an age of 0. For instance, if we consider an agent that is currently 60 years old, then .
Notice that risk aversion coefficients below unity are unrealistic. See, e.g., Munk (2013).
Our model ends at , but we could extend it to .
Notice that should be interpreted as numbers here.
See, e.g., Walter (1998), p. 108.
See, e.g., Munk (2013), p. 187, for further details.
See also Kraft, Seifried, & Seiferling (2017).
This is in line with the literature and implies a moderate weight on bequest. See, e.g., Kraft, Munk, & Weiss (2022).
https://www.ssa.gov/oact/STATS/table4c6.html#fn1. The table is available upon request.
https://data.cdc.gov/NCHS/Provisional-COVID-19-Death-Counts-by-Sex-Age-and-W/vsak-wrfu. See also Table 3 in Online Appendix D.
See, e.g., Huremovic (2019) or https://www.cdc.gov/flu/pandemic-resources/basics/past-pandemics.html. Table 4 in the Online Appendix D summarizes these pandemics.
These constant costs are for instance equivalent to a set of beta-distributed costs. More details can be found in Online Appendix A.
We average over the risk-free rate reported by Kenneth French. Real values are achieved by subtracting the change in the CPI.
The differences in mortality risk between males and females do not lead to significant differences in the optimal consumption and investment decisions. Additional results for the age between 20 and 60 can be found in Online Appendix E.
See, e.g., Munk (2013) for a definition of precautionary savings.
Additional tables are available upon request.
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.ejor.2022.05.035.
Notice that is bounded from above by 0.
Appendix A. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- Ait-Sahalia Y., Cacho-Diaz J., Hurd T. Portfolio choice with jumps: A closed-form solution. Annals of Applied Probability. 2009;19:556–584. [Google Scholar]
- Ait-Sahalia Y., Hurd T. Portfolio choice in markets with contagion. Journal of Financial Econometrics. 2016;14(1):1–28. [Google Scholar]
- Ang A., Bekaert G. International asset allocation with regime shifts. Review of Financial Studies. 2002;15(4):1137–1187. [Google Scholar]
- Bäuerle N., Rieder U. Portfolio optimization with jumps and unobservable intensity process. Mathematical Finance. 2007;17(2):205–224. [Google Scholar]
- Bäuerle N., Rieder U. MDP algorithms for portfolio optimization problems in pure jump markets. Finance and Stochastics. 2009;13(4):591–611. [Google Scholar]
- Bick B., Kraft H., Munk C. Solving constrained consumption-investment problems by simulation of artificial market strategies. Management Science. 2013;59:485–503. [Google Scholar]
- Chen A., Vellekoop M. Optimal investment and consumption when allowing terminal debt. European Journal of Operational Research. 2017;258:385–397. [Google Scholar]
- Duffie D., Epstein L.G. Stochastic differential utility. Econometrica. 1992;60:353–394. [Google Scholar]
- French E., Jones J.B. On the distribution and dynamics of health care costs. Journal of Applied Econometrics. 2004;19:705–721. [Google Scholar]
- Fu J., Wei J., Yang H. Portfolio optimization in a regime-switching market with derivatives. European Journal of Operational Research. 2014;233:184–192. [Google Scholar]
- Guidolin M., Timmermann A. International asset allocation under regime switching, skew and kurtosis preferences. Review of Financial Studies. 2008;21(2):889–935. [Google Scholar]
- Honda T. Optimal portfolio choice for unobservable and regime-switching mean returns. Journal of Economic Dynamics and Control. 2003;28:45–78. [Google Scholar]
- Huremovic D. Springer; 2019. Brief history of pandemics (pandemics throughout history) pp. 7–35. [Google Scholar]
- Kamma T., Pelsser A. Near-optimal asset allocation in financial markets with trading constraints. European Journal of Operational Research. 2021;297:766–781. [Google Scholar]
- Kolm P.N., Tütüncü R., Fabozzi F.J. 60 Years of portfolio optimization: Practical challenges and current trends. European Journal of Operational Research. 2014;234:356–371. [Google Scholar]
- Korn R., Kraft H. A stochastic control approach to portfolio problems with stochastic interest rates. SIAM Journal on Control and Optimization. 2001;40:1250–1269. [Google Scholar]
- Kraft H., Munk C., Weiss F. Bequest motives in consumption-portfolio decisions with recursive utility. Journal of Banking and Finance. 2022;138:106428. [Google Scholar]
- Kraft H., Seifried F.T., Seiferling T. Optimal consumption and investment with Epstein-Zin recursive utility. Finance and Stochastics. 2017;21:187–226. [Google Scholar]
- Kraft H., Seifried F.T., Steffensen M. Consumption-portfolio optimization with recursive utility in incomplete markets. Finance and Stochastics. 2013;17:161–196. [Google Scholar]
- Kraft H., Steffensen M. Asset allocation with contagion and explicit bankruptcy procedures. Journal of Mathematical Economics. 2009;45:147–167. [Google Scholar]
- Kraft H., Steffensen M. A dynamic programming approach to constrained portfolios. European Journal of Operational Research. 2013;229:453–461. [Google Scholar]
- Liesiöa J., Salo A., Keisler J.M., Morton A. Portfolio decision analysis: Recent developments and future prospects. European Journal of Operational Research. 2021;293:811–825. [Google Scholar]
- Liu J., Chen Z. Time consistent multi-period robust risk measures and portfolio selection models with regime-switching. European Journal of Operational Research. 2018;268:373–385. [Google Scholar]
- Liu J., Longstaff F.A., Pan J. Dynamic asset allocation with event risk. Journal of Finance. 2003;58:231–259. [Google Scholar]
- Merton R.C. Lifetime portfolio selection under uncertainty: The continuous case. Reviews of Economical Statistics. 1969;51:247–257. [Google Scholar]
- Merton R.C. Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory. 1971;3:373–413. [Google Scholar]
- Munk C. Oxford University Press; 2013. Financial asset pricing theory. [Google Scholar]
- Sass J., Haussmann U.G. Optimizing the terminal wealth under partial information: The drift process as a continuous time Markov chain. Finance and Stochastics. 2004;8:553–577. [Google Scholar]
- Sotomayor L.R., Cadenillas A. Explicit solutions of consumption-investment problems in financial market with regime switching. Mathematical Finance. 2009;19:251–279. [Google Scholar]
- Walter W. Springer; 1998. Ordinary differential equations. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/