Robust Integral Sliding Mode Control for Fuzzy Stochastic Impulsive Systems | International Journal of Fuzzy Systems Skip to main content

Advertisement

Springer Nature Link
Log in

Robust Integral Sliding Mode Control for Fuzzy Stochastic Impulsive Systems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

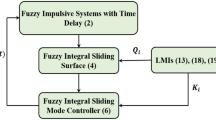
This paper investigates the sliding mode control problem for Takagi–Sugeno (T–S) fuzzy stochastic impulsive systems. Since considered T–S fuzzy systems contain stochastic impulses, a new continuous fuzzy integral sliding surface is designed so that its reachability is ensured for any a given time. Based on the designed fuzzy integral sliding surface, a fuzzy sliding mode controller is developed, which can guarantee the exponential stability of T–S fuzzy stochastic impulsive system. By constructing an appropriate Lyapunov function, the exponential stability conditions of T–S fuzzy stochastic impulsive systems are established in the form of linear matrix inequalities. Consequently, a control design algorithm is formulated based on the established the exponential stability conditions. Finally, two simulation examples and comparisons are provided to check the effectiveness of the proposed fuzzy SMC scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Li, X.D., Cao, J.D.: An impulsive delay inequality involving unbounded time-varying delay and applications. IEEE Trans. Autom. Control 62(7), 3618–3625 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  2. Luo, S.X., Deng, F.Q., Chen, W.H.: Stability and stabilization of linear impulsive systems with large impulse-delays: a stabilizing delay perspective. Automatica (2021). https://doi.org/10.1016/j.automatica.2021.109533

    Article  MATH  Google Scholar 

  3. Zamani, I., Shafiee, M., Ibeas, A.: On singular hybrid switched and impulsive systems. Int. J. Robust Nonlinear Control 28(2), 437–465 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Lu, X.D., Li, H.T., Wang, C.K., Zhang, X.F.: Stability analysis of positive switched impulsive systems with delay on time scales. Int. J. Robust Nonlinear Control 30(16), 6879–6890 (2020)

    Article  MathSciNet  Google Scholar 

  5. Luo, S.X., Deng, F.Q., Chen, W.H.: Stability analysis and synthesis for linear stochastic impulsive systems. Int. J. Robust Nonlinear Control 28(15), 4424–4437 (2018)

    Article  MATH  Google Scholar 

  6. Li, Y.E., Zhang, H.S., Zhang, T.T., Geng, H.: Interval stability/stabilization and H∞ feedback control for linear stochastic impulsive systems. Appl. Math. Comput. 437, 127552 (2023)

    MATH  Google Scholar 

  7. Chen, W.H., Wang, J.G., Tang, Y.J., Lu, X.M.: Robust H∞ control of uncertain linear impulsive stochastic systems. Int. J. Robust Nonlinear Control 18(13), 1348–1371 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Takagi, T., Sugeno, M.: Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1, 116–132 (1985)

    Article  MATH  Google Scholar 

  9. Su, X.J., Shi, P., Wu, L.G., Song, Y.D.: A novel approach to filter design for T-S fuzzy discrete-time systems with time-varying delay. IEEE Trans. Fuzzy Syst. 20(6), 1114–1129 (2012)

    Article  Google Scholar 

  10. Cai, X., Zhong, S.M., Wang, J., Shi, K.B.: Robust H∞ control for uncertain delayed T-S fuzzy systems with stochastic packet dropouts. Appl. Math. Comput. 385, 125432 (2020)

    MathSciNet  MATH  Google Scholar 

  11. Sheng, Y., Lewis, F.L., Zeng, Z.G., Huang, T.W.: Stability and stabilization of Takagi-Sugeno fuzzy systems with hybrid time-varying delays. IEEE Trans. Fuzzy Syst. 27(10), 2067–2078 (2019)

    Article  Google Scholar 

  12. Lee, S.: Novel stabilization criteria for T-S fuzzy systems with affine matched membership functions. IEEE Trans. Fuzzy Syst. 27(3), 540–548 (2018)

    Article  MathSciNet  Google Scholar 

  13. Wang, L.K., Lam, H.K.: New stability criterion for continuous-time Takagi–Sugeno fuzzy systems with time-varying delay. IEEE Trans. Cybern. 49(4), 1551–1556 (2018)

    Article  Google Scholar 

  14. Ho, D.W.C., Sun, J.T.: Stability of Takagi-Sugeno fuzzy delay systems with impulse. IEEE Trans. Fuzzy Syst. 15(5), 784–790 (2007)

    Article  Google Scholar 

  15. Hu, M.J., Park, J.H., Wang, Y.W.: Stabilization of positive systems with time delay via the Takagi–Sugeno fuzzy impulsive control. IEEE Trans. Cybern. 52(6), 4275–4285 (2020)

    Article  Google Scholar 

  16. Yu, J.J., Zhang, K.J., Fei, S.M., Jiang, H.B.: Robust fuzzy control of nonlinear stochastic delay systems with impulsive effects. Int. J. Syst. Sci. 41(10), 1163–1172 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gao, Q., Liu, L., Feng, G., Wang, Y., Qiu, J.B.: Universal fuzzy integral sliding-mode controllers based on T-S fuzzy models. IEEE Trans. Fuzzy Syst. 22(2), 350–362 (2013)

    Article  Google Scholar 

  18. Gao, Q., Liu, L., Feng, G., Wang, Y.: Universal fuzzy integral sliding-mode controllers for stochastic nonlinear systems. IEEE Trans. Cybern. 44(12), 2658–2669 (2014)

    Article  Google Scholar 

  19. Wang, Y.Y., Xia, Y.Q., Li, H.Y., Zhou, P.F.: A new integral sliding mode design method for nonlinear stochastic systems. Automatica 90, 304–309 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ho, D.W.C., Niu, Y.G.: Robust fuzzy design for nonlinear uncertain stochastic systems via sliding-mode control. IEEE Trans. Fuzzy Syst. 15(3), 350–358 (2007)

    Article  Google Scholar 

  21. Gao, Q., Feng, G., Liu, L., Qiu, J.B., Wang, Y.: Robust control for stochastic T-S fuzzy systems via integral sliding-mode approach. IEEE Trans. Fuzzy Syst. 22(4), 870–881 (2013)

    Article  Google Scholar 

  22. Chen, W.H., Deng, X.Q., Zheng, W.X.: Sliding-mode control for linear uncertain systems with impulse effects via switching gains. IEEE Trans. Autom. Control 67(4), 2044–2051 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  23. Niu, S.N., Chen, W.H., Lu, X.M.: Sliding mode control with integral sliding surface for linear uncertain impulsive systems with time delays. Appl. Math. Model. 113, 439–455 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  24. Li, X.D., Zhao, Y.S.: Sliding mode control for linear impulsive systems with matched disturbances. IEEE Trans. Autom. Control 67(11), 6203–6210 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was funded by National Natural Science Foundation of China (Grant Nos. 62173172 and U22A2043).

Author information

Authors and Affiliations

  1. College of Science, Liaoning University of Technology, Jinzhou, China

    Lei Song, Yongming Li & Shaocheng Tong

Authors
  1. Lei Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yongming Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shaocheng Tong
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shaocheng Tong.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, L., Li, Y. & Tong, S. Robust Integral Sliding Mode Control for Fuzzy Stochastic Impulsive Systems. Int. J. Fuzzy Syst. 25, 2555–2567 (2023). https://doi.org/10.1007/s40815-023-01572-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-023-01572-4

Keywords