A study of turbine failure pattern: a model optimization using machine learning

Abstract

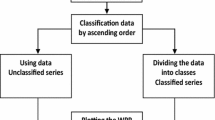
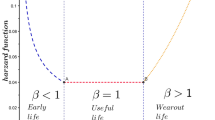
With the growing demand of electricity worldwide, most of the power generation companies focus on long-term and cost-effective asset operation and maintenance strategies to reduce their unplanned downtime which is their main cost driver. Power generating companies are trying to make their commercial process smart and agile enough to do proactive equipment assessment and failure identification in advance rather than taking corrective actions after an event. A turbine failure occurs when a turbine unexpectedly stops producing power due to malfunctioning or break-down of the key components. This creates a complete shutdown of the power generation process and disruption in power generation. To keep these operational, it is extremely important to have a robust asset reliability and failure prediction models which can pro-actively help these companies to manage their operation and maintenance costs optimally. In this paper, we have studied the failure pattern of turbines after fitting most commonly used single distribution (such as Weibull, gamma and log-normal) and also composite and mixed distributions by the help of machine learning tools to forecast asset failure patterns more accurately. The paper finally compares between single distribution model fitting with composite and mixed distribution model fitting. The numerical illustration is based on historical failure data of 2470 turbines. More importantly, if more than one suitable model exists, the same can be mathematically combined to get a joint forecast model to forecast failure pattern which is found better than single distribution applied separately. Finally, these predictive methods could be applied to a power generating company for the failure forecast of its assets and to identify upcoming commercial action in advance.