Reliability analysis of log-normal distribution with nonconstant parameters under constant-stress model

Abstract

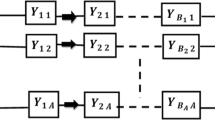
Under constant-stress accelerated life test, the general progressive type-II censoring sample and the two parameters following the linear Arrhenius model, the point estimation and interval estimation of the two parameters log-normal distribution were discussed. The unknown parameters of the model as well as reliability and hazard rate functions are estimated by using Maximum likelihood (ML) and Bayesian methods. The maximum-likelihood estimates are derived by the Newton–Raphson method and the corresponding asymptotic variance is derived by the Fisher information matrix. Since the Bayesian estimates (BEs) of the unknown parameters cannot be expressed explicitly, the approximate BEs of the unknown parameters. The approximate highest posterior density confidence intervals are calculated. The practicality of the proposed method is illustrated by simulation study and real data application analysis.

Appendix  A

Let $\xi _i(\mu )=\frac{\ln x_{i:r_{i}+1}-\mu \theta _{1}^{\phi _{i}}}{\sigma {\theta _{2}}^{\phi _{i}}},$ $\xi _{i:j}(\mu )=\frac{\ln x_{i:j}-\mu \theta _{1}^{\phi _{i}}}{\sigma {\theta _{2}}^{\phi _{i}}}, i=1,\ldots ,k,~j=r_{i}+1,\ldots ,m_i,$ we have that

$$\begin{aligned} \frac{\partial \log \pi (\mu | \sigma ,\theta _{1},\theta _{2},{\varvec{x}})}{\partial \mu }= & {} \sum \limits _{i=1}^{k}\frac{r_{i}\cdot \varphi [\xi _i(\mu )] \cdot \xi _i'(\mu )}{\Phi [\xi _i(\mu )]}\\&-\sum \limits _{i=1}^{k}\!\!\sum \limits _{j=r_{i}+1}^{m_{i}}\left\{ \xi _{i:j}(\mu )\cdot \xi _{i:j}'(\mu ) +\frac{R_{i:j}\cdot \varphi [\xi _{i:j}(\mu )]\cdot \xi _{i:j}'(\mu )}{1-\Phi [\xi _{i:j}(\mu )]} \right\} +\frac{\mathrm{d}log\pi (\mu )}{\mathrm{d}\mu }.\\ \frac{\partial ^2\log \pi (\mu | \sigma ,\theta _{1},\theta _{2},{\varvec{x}})}{\partial \mu ^2}= & {} \sum \limits _{i=1}^{k}r_{i}\cdot \frac{\partial \left( \frac{\varphi [\xi _i(\mu )]\cdot \xi _i'(\mu )}{\Phi [\xi _i(\mu )]}\right) }{\partial \mu }\\&-\sum \limits _{i=1}^{k}\!\!\sum \limits _{j=r_{i}+1}^{m_{i}} \left\{ \{\xi _{i:j}'(\mu )\}^2 + R_{i:j}\cdot \frac{\partial \Big (\frac{\varphi [\xi _{i:j}(\mu )]\cdot \xi _{i:j}'(\mu )}{1-\Phi [\xi _{i:j}(\mu )]}\Big )}{\partial \mu } \right\} +\frac{\mathrm{d}^2log\pi (\mu )}{\mathrm{d}\mu ^2}. \end{aligned}$$

First, in Eq. (31), $\frac{\mathrm{d}^2log\pi (\mu )}{\mathrm{d}\mu ^2}\le 0$ because $\pi (\mu )$ is log-concave. Next, we demonstrate that $\frac{\partial \Big (\frac{\varphi [\xi _i(\mu )]\cdot \xi _i'(\mu )}{\Phi [\xi _i(\mu )]}\Big )}{\partial \mu }\le 0$ and $\frac{\partial \Big (\frac{\varphi [\xi _{i:j}(\mu )]\cdot \xi _{i:j}'(\mu )}{1-\Phi [\xi _{i:j}(\mu )]}\Big )}{\partial \mu } \ge 0.$

Without loss of generality, let $A(\mu )=\frac{\ln x-\mu \theta _{1}^{\phi }}{\sigma {\theta _{2}}^{\phi }}$, we have that

$$\begin{aligned} A'(\mu )=-\frac{\theta _{1}^{{\phi }}}{\sigma {\theta _{2}}^{\phi }}<0,\quad \varphi '[A(\mu )]=\frac{{\mathrm{d}}\varphi [A(\mu )]}{{\mathrm{d}}A(\mu )}=-\varphi [A(\mu )]\cdot A(\mu ). \end{aligned}$$

And

$$\begin{aligned} \frac{\partial \Big (\frac{\varphi [A(\mu )]\cdot A'(\mu )}{\Phi [A(\mu )]}\Big )}{\partial \mu }= & {} \frac{\varphi '[A(\mu )]\cdot \{A'(\mu )\}^2\cdot \Phi [A(\mu )] -\{\varphi [A(\mu )]\cdot A'(\mu )\}^2}{\Phi ^2[A(\mu )]}\\= & {} \frac{-\varphi [A(\mu )]\cdot A(\mu ) \cdot \{A'(\mu )\}^2\cdot \Phi [A(\mu )] -\{\varphi [A(\mu )]\cdot A'(\mu )\}^2}{\Phi ^2[A(\mu )]}\\= & {} \frac{-\varphi [A(\mu )]\cdot \{A'(\mu )\}^2 \cdot \{A(\mu )\cdot \Phi [A(\mu )]+\varphi [A(\mu )]\}}{\Phi ^2[A(\mu )]}\\= & {} \frac{-\varphi [A(\mu )]\cdot \{A'(\mu )\}^2 \cdot g_1(\mu )}{\Phi ^2[A(\mu )]},\\ \end{aligned}$$

where $g_1(\mu )=A(\mu )\cdot \Phi [A(\mu )]+\varphi [A(\mu )]$. Then

$$\begin{aligned} g'_1(\mu )= & {} A'(\mu )\cdot \Phi [A(\mu )] +A(\mu )\cdot \varphi [A(\mu )]\cdot A'(\mu ) -\varphi [A(\mu )]\cdot A(\mu )\cdot A'(\mu )\\= & {} A'(\mu )\cdot \Phi [A(\mu )]<0. \end{aligned}$$

Namely, $g_1(\mu )$ is decreasing about $\mu$. Apparently,

$$\begin{aligned} \lim _{\mu \rightarrow +\infty } A(\mu )=-\infty , \lim _{\mu \rightarrow +\infty }\Phi [A(\mu )]=0, \lim _{\mu \rightarrow +\infty }\varphi [A(\mu )]=0 \end{aligned}$$

By simply taking the limit, we can get

$$\begin{aligned} \lim _{\mu \rightarrow +\infty } A(\mu )\cdot \Phi [A(\mu )]= & {} \lim _{\mu \rightarrow +\infty } \frac{A(\mu )}{\frac{1}{\Phi [A(\mu )]}}\\= & {} \lim _{\mu \rightarrow +\infty } \frac{A'(\mu )}{\frac{-\varphi [A(\mu )]\cdot A'(\mu )}{\Phi ^2[A(\mu )]}}\\= & {} \lim _{\mu \rightarrow +\infty } \frac{-\Phi ^2[A(\mu )]}{\varphi [A(\mu )]}\\= & {} \lim _{\mu \rightarrow +\infty } \frac{2\Phi [A(\mu )]\cdot \varphi [A(\mu )]\cdot A'(\mu )}{\varphi [A(\mu )]\cdot A(\mu )\cdot A'(\mu )}\\= & {} \lim _{\mu \rightarrow +\infty } \frac{2\Phi [A(\mu )]}{ A(\mu )}\\= & {} 0. \end{aligned}$$

Therefore, $g_1(\mu )\ge 0$. Thus, $\frac{\partial \Big (\frac{\varphi [A(\mu )]\cdot A'(\mu )}{\Phi [A(\mu )]}\Big )}{\partial \mu }\le 0$.

$$\begin{aligned} \frac{\partial \Big (\frac{\varphi [A(\mu )]\cdot A'(\mu )}{1-\Phi [A(\mu )]}\Big )}{\partial \mu }= & {} \frac{\varphi '[A(\mu )]\cdot \{A'(\mu )\}^2\cdot \{1-\Phi [A(\mu )]\} +\{\varphi [A(\mu )]\cdot A'(\mu )\}^2}{\{1-\Phi [A(\mu )]\}^2}\\= & {} \frac{-\varphi [A(\mu )]\cdot A(\mu ) \cdot \{A'(\mu )\}^2\cdot \{1-\Phi [A(\mu )]\} +\{\varphi [A(\mu )]\cdot A'(\mu )\}^2}{\{1-\Phi [A(\mu )]\}^2}\\= & {} \frac{-\varphi [A(\mu )]\cdot \{A'(\mu )\}^2 \cdot \bigg (A(\mu )\cdot \{1-\Phi [A(\mu )]\}-\varphi [A(\mu )]\bigg )}{\{1-\Phi [A(\mu )]\}^2}\\= & {} -\frac{\varphi [A(\mu )]\cdot \{A'(\mu )\}^2 \cdot g_2(\mu )}{\{1-\Phi [A(\mu )]\}^2}.\\ \end{aligned}$$

where $g_2(\mu )=A(\mu )\cdot \{1-\Phi [A(\mu )]\}-\varphi [A(\mu )]$, then

$$\begin{aligned} g'_2(\mu )= & {} A'(\mu )\cdot \{1-\Phi [A(\mu )]\} -A(\mu )\cdot \varphi [A(\mu )]\cdot A'(\mu ) +\varphi [A(\mu )]\cdot A(\mu )\cdot A'(\mu )\\= & {} A'(\mu )\cdot \{1-\Phi [A(\mu )]\}<0. \end{aligned}$$

Therefore, $g_2(\mu )$ is decreasing about $\mu$. Apparently, we have

$$\begin{aligned} \lim _{\mu \rightarrow +\infty } A(\mu )=-\infty , \lim _{\mu \rightarrow +\infty }\{1-\Phi [A(\mu )]\}=1, \lim _{\mu \rightarrow +\infty }\varphi [A(\mu )]=0. \end{aligned}$$

It indicates that

$$\begin{aligned} \lim _{\mu \rightarrow +\infty } g_2(\mu ) =-\infty . \end{aligned}$$

Further, we have

$$\begin{aligned} \lim _{\mu \rightarrow -\infty } A(\mu )=+\infty , \lim _{\mu \rightarrow -\infty }\{1-\Phi [A(\mu )]\}=0, \lim _{\mu \rightarrow -\infty }\varphi [A(\mu )]=0. \end{aligned}$$

Let’s do the simple limit again,

$$\begin{aligned} \lim _{\mu \rightarrow -\infty } g_2(\mu )= & {} \lim _{\mu \rightarrow +\infty }\frac{A(\mu )}{\frac{1}{\{1-\Phi [A(\mu )]\}}}\\= & {} \lim _{\mu \rightarrow +\infty }\frac{\{1-\Phi [A(\mu )]\}^2}{\varphi [A(\mu )]}\\= & {} \lim _{\mu \rightarrow +\infty }\frac{2\{1-\Phi [A(\mu )]\}\cdot \varphi [A(\mu )]\cdot A'(\mu )}{\varphi [A(\mu )]\cdot A(\mu )\cdot A'(\mu )}\\= & {} 0. \end{aligned}$$

We obtain that $g_2(\mu )\le 0$, further $\frac{\partial \Big (\frac{\varphi [A(\mu )]\cdot A'(\mu )}{1-\Phi [A(\mu )]}\Big )}{\partial \mu }\ge 0$. Hence, $\frac{\partial ^2\log \pi (\mu |\sigma ,\theta _{1},\theta _{2},{\varvec{x}})}{\partial \mu ^2}\le 0$, namely, $\pi (\mu |\sigma ,\theta _{1},\theta _{2},{\varvec{x}})$ is log-concave.