Abstract
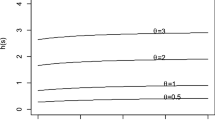
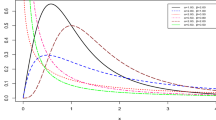
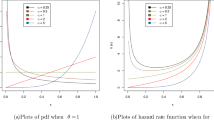
This study deals with the classical and Bayesian analysis of the hybrid censored lifetime data under the assumption that the lifetime follow Lindley distribution. In classical set up, the maximum likelihood estimate of the parameter with its standard error are computed. Further, by assuming Jeffrey’s invariant and gamma priors of the unknown parameter, Bayes estimate along with its posterior standard error and highest posterior density credible intervals of the parameter are obtained. Markov Chain Monte Carlo technique such as Metropolis–Hastings algorithm has been utilized to generate draws from the posterior density of the parameter. A real data set representing the waiting time of the bank customers has been analyzed for illustration purpose. A comparison study is conducted to judge the performance of the classical and Bayesian estimation procedure.







Similar content being viewed by others
References
Al-Mutairi DK, Ghitany ME, Kundu D (2011) Inference on stress-strength reliability from Lindley distribution. http://home.iitk.ac.in/~kundu/lindley-ss.pdf. Accessed 10 Feb 2012
Balakrishnan N, Aggarwala R (2000) Progressive censoring: theory, methods and applications. Birkhauser, Boston
Banerjee A, Kundu D (2008) Inference based on Type-II hybrid censored data from a Weibull. IEEE Trans Rel 57(2):369–379
Chen SM, Bhattacharya GK (1988) Exact confidence bounds for an exponential parameter hybrid censoring. Commun Stat Theory Methods 17(6):1858–1870
Chen MH, Shao QM (1999) Monte Carlo estimation of Bayesian credible and HPD intervals. J Comput Graph Stat 6:69–92
Childs A, Chandrasekhar B, Balakrishnan N, Kundu D (2003) Exact likelihood inference based on type-I and type-II hybrid censored samples from the exponential distribution. Ann Inst Stat Math 55:319–330
Draper N, Guttman I (1987) Bayesian analysis of hybrid life tests with exponential failure times. Ann Inst Stat Math 39:219–225
Dube S, Pradhan B, Kundu D (2011) Parameter estimation for the hybrid censored log-normal distribution. J Stat Comput Simul 81(3):275–282
Epstein B (1954) Truncated life-tests in the exponential case. Ann Math Stat 25:555–564
Ganguly et al (2012) Exact inference for the two-parameter exponential distribution under type-II hybrid censoring scheme. J Stat Plan Inf 142(3):613–625
Ghitany ME, Atieh B, Nadarajah S (2008) Lindley distribution and its application. Math Comput Simul 78(4):493–506
Gomoz-Deniz E, Calderin-Ojeda E (2011) The discrete Lindley distribution: properties and applications. J Stat Comput Simul 81(11):1405–1416
Singh B, Gupta, PK (2012) Load-sharing system model and its application to the real data set. Math Comput Simul. http://dx.doi.org/10.1016/j.matcom.2012.02.010
Gupta RD, Kundu D (1998) Hybrid censoring schemes with exponential failure distribution. Commun Stat Theory Methods 27:3065–3083
Krishna H, Kumar K (2011) Reliability estimation in Lindley distribution with progressively type II right censored sample. Math Comput Simul 82(2):281–294
Kundu D (2007) On hybrid censored Weibull distribution. J Stat Plan Inference 137:2127–2142
Kundu D, Pradhan B (2009) Estimating the parameters of the generalized exponential distribution in presence of the hybrid censoring. Commun Stat Theory Methods 38(12):2030–2041
Lindley DV (1958) Fiducial distribution and Bayes’ theorem. J Roy Stat Soc 20(2):102–107
Mazucheli J, Achcar JA (2011) The Lindley distribution applied to competing risks lifetime data. Comput Methods Programs Biomed 104(2):188–192
MIL-STD-781-C (1977) Reliability design qualifications and production acceptance test. Exponential distribution. U.S. Government Printing Office, Washington, DC
Wu SJ, Chang CT (2003) Inference in the Pareto distribution based on progressive Type II censoring with random removals. J Appl Stat 30(2):163–172
Acknowledgments
The authors thankfully acknowledge the critical suggestions and comments from the learned referee which greatly helped us in the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gupta, P.K., Singh, B. Parameter estimation of Lindley distribution with hybrid censored data. Int J Syst Assur Eng Manag 4, 378–385 (2013). https://doi.org/10.1007/s13198-012-0120-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-012-0120-y