Abstract
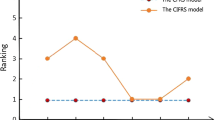
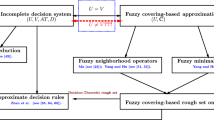
There are many extensions of Pawlak’s rough sets. Particularly, fuzzy rough set theory based on residuated lattices is considered as one of the generalizations that extends the truth values to lattices. In this paper, we attempt to combine the idea of “variable precision” with covering-based fuzzy rough sets based on residuated lattices and present the concept of covering-based variable precision L-fuzzy rough sets. After the presentation of this concept, some basic properties of the proposed rough set model are discussed. Then, with the aid of the PROMETHEE and TOPSIS methods, we put forth a novel multi-attribute decision-making (MADM) method based on covering-based variable precision L-fuzzy rough sets (for \(L=[0,1]\)). Finally, an illustrative example is give to demonstrate the proposed decision-making method. By a sensitivity analysis along with a comparative analysis, we reveal the applicability and validity of the proposed decision-making method.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
A t-norm \(\top\) is a binary function on [0, 1] if it is commutative, associative, non-decreasing and meets \(\top (1,o)=o\) for each \(o\in [0,1]\).
An implicator is a binary function \(\theta\) on [0, 1] if for all \(o\in [0,1]\), \(\theta (\cdot , o)\) is non-increasing, \((o,\cdot )\) is non-decreasing and meets \(\theta (1,0)=0\), \(\theta (1,1)=\theta (0,1)=\theta (0,0)=1\).
We name \(L=([0,1],\otimes ,\rightarrow ,\vee ,\wedge ,0,1)\) is a Łukasiewicz reriduated lattice if \(m\otimes n=\max \{ 0, m+n-1\}\), \(m\rightarrow n=\min \{1-m+n,1\}\) for any \(m,n\in L.\)
References
Brans JP, Vincke P, Mareschal B (1986) How to select and how to rank projects: the PROMETHEE method. Eur J Oper Res 24:228–238
Chen CT (2000) Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst 114:1–9
Chen DG, Wang CZ, Hu QH (2007) A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets. Inform Sci 177:3500–3518
Dai JH, Chen JL (2020) Feature selection via normative fuzzy information weight with application into tumor classification. Appl Soft Comput 92:106299
Dai JH, Han H, Hu Q, Liu M (2016) Discrete particle swarm optimization approach for cost sensitive attribute reduction. Knowl.-Based. Syst. 102:116–126
Dai JH, Hu H, Wu WZ, Qian YH, Huang DB (2018) Maximal discernibility pairs based approach to attribute reduction in fuzzy rough sets. IEEE Trans Fuzzy Syst 26(4):2174–2187
Deer L, Cornelis C (2018) A comprehensive study of fuzzy covering-based rough set models: Definitions, properties and interrelationships. Fuzzy Sets Syst 336:1–26
Deer L, Cornelis C, Godo L (2017) Fuzzy neighborhood operators based on fuzzy covering. Fuzzy Sets Syst 312:17–35
Deng TQ, Chen YM, Xu WL, Dai QH (2007) A novel approach to fuzzy rough sets based on a fuzzy covering. Inform. Sci. 177:2308–2326
Dubois D, Prade H (1990) Rough fuzzy sets and fuzzy rough sets. Int J Gen Syst 17:191–209
Dyer JS, Fishburn PC, Steuer RE, Wallenius J, Zionts S (1992) Multiple criteria decision making, multi-attribute utility theory: the next ten years. Manage Sci 38:645–654
Figueira J, Greco S, Ehrgott M (2005) Multiple criteria decision analysis: state of the art surveys. Springer, New York
Goguen JA (1967) \(L\)-fuzzy sets. J Math Anal Appl 18:145–174
Goumas M, Lygerou V (2000) An extension of the PROMETHEE method for decision making in fuzzy environment: ranking of alternative energy exploitation projects. Eur J Oper Res 123:606–613
Hadi-Vencheh A, Mirjaberi M (2014) Fuzzy inferior ratio method for multiple attribute decision making problem. Inform. Sci. 277:263–272
Harsanyi JC (1955) Cardinal welfare, individualistic ethics and interpersonal comparisons of utility. J Political Econ 63:309–321
Hu QH, An S, Yu DR (2011) Robust fuzzy rough classifiers. Fuzzy Sets Syst 183:26–43
Hwang CL, Yoon K (1981) Multiple attributes decision making methods and applications. Springer, Berlin Heidelberg
Jensen R, Shen Q (2004) Fuzzy-rough attributes reduction with application to web categorization. Fuzzy Sets Syst 141:469–485
Jiang HB, Zhan JM, Chen DG (2020) PROMETHEE II method based on variable precision fuzzy rough sets with fuzzy neighborhoods. Artif Intell Rev. https://doi.org/10.1007/s10462-020-09878-7
Jiang HB, Zhan JM, Sun BZ, Alcantud JCR (2020) An MADM approach to covering-based variable precision fuzzy rough sets: an application to medical diagnosis. Int J Mach Learn Cyb 11:2181–2207
Li LQ, Jin Q, Hu K, Zhao FF (2017) The axiomatic characterizations on \(L\)-fuzzy covering-based approximation operators. Int J Gen Syst 46:332–353
Li TJ, Leung Y, Zhang WX (2008) Generalized fuzzy rough approximation operators based on fuzzy coverings. Int J Approx Reason 48:836–856
Liang DC, Wang MW, Xu ZS (2019) Heterogeneous multi-attribute nonadditivity fusion for behavioral three-way decisions in interval type-2 fuzzy environment. Inform Sci 496:242–263
Liang DC, Xu ZS, Liu D, Wu Y (2018) Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inform Sci 435:282–295
Liao HC, Xu ZS (2014) Multi-criteria decision making with intuitionistic fuzzy PROMETHEE. J Intell Fuzzy Syst 27:1703–1717
Ma LW (2016) Two fuzzy covering rough set models and their generalizations over fuzzy lattices. Fuzzy Sets Syst 294:1–17
Mardani A, Jusoh A, Zavadskas EK, Fuzzy multiple criteria decision-making techniques and applications-Two decades review from, (1994) to 2014. Expert Syst Appl 42(2015):4126–4148
Meng FY, Tang J, Fujita H (2019) Linguistic intuitionistic fuzzy preference relations and their application to multi-criteria decision making. Inform. Fusion 46:77–90
Merigo JM, Gil-Lafuente AM (2010) New decision-making techniques and their application in the selection of financial products. Inform Sci 180:2085–2094
Opricovic S, Tzeng GH (2004) Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur J Oper Res 156:445–455
Palmeira E, Bedregal B, Mesiar R, Fernandez J (2014) A New Way to Extend t-norms, t-conorms and Negations. Fuzzy Sets Syst 240:1–21
Pamučar D, Petrović I, Ćirović G (2018) Modification of the Best-Worst and MABAC methods: a novel approach based on interval-valued fuzzy-rough numbers. Expert Syst Appl 91:89–106
Pawlak Z (1982) Rough sets. Int J Comput Inform Sci 11:341–356
Qiao JS, Hu BQ (2018) Granular variable precision \(L\)-fuzzy rough sets based on residuated lattices. Fuzzy Sets Syst 336:148–166
A.M. Radzikowska, E.E. Kerre, Fuzzy rough sets based on residuated lattices, in: Transactions on Rough Sets II, in: Lect. Notes Comput. Sci., vol 3155, Springer-Verlag, 2004, pp. 278-296
Ramalho FD, Ekel PY, Pedrycz W, Júnior JGP, Soares GL (2019) Multicriteria decision making under conditions of uncertainty in application to multiobjective allocation of resources. Inform Fusion 49:249–261
Roy B (1968) Classement et choix en présence de ponts de vue multiples (la méthode ELECTRE) Rev. Fr Inf Rech Opér 8:57–75
Sun BZ, Ma WM, Li BJ, Li XN (2018) Three-way decisions approach to multiple attribute group decision making with linguistic information-based decision-theoretic rough fuzzy set. Int J Approx Reason 93:424–442
Sun BZ, Ma WM, Qian YH (2017) Multigranulation fuzzy rough set over two universes and its application to decision making. Knowl-Based Syst 123:61–74
Sun BZ, Zhou XM, Lin NN (2020) Diversified binary relation-based fuzzy multigranulation rough set over two universes and application to multiple attribute group decision making. Inform Fusion 55:91–104
Wang CY, Hu BQ (2015) Granular variable precision fuzzy rough sets with general fuzzy relations. Fuzzy Sets Syst 275:39–57
Wang CZ, Wang Y, Shao MW, Qian YH, Chen DG (2020) Fuzzy rough attribute reduction for categorical data. IEEE Tran Fuzzy Syst 28:818–830
Wang XZ, Tsang ECC, Zhao SY, Chen DG, Yeung DS (2007) Learning fuzzy rules from fuzzy samples based on rough set technique. Inform Sci 177:4493–4514
Wei W, Liang JY (2019) Information fusion in rough set theory: an overview. Inform Fusion 48:107–118
Xu ZS, Zhao N (2016) Information fusion for intuitionistic fuzzy decision making: An overview. Inform Fusion 28:10–23
Yager RR (1988) On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Tran Fuzzy Syst 18:183–190
Yager RR (1993) Families of OWA operators. Fuzzy Sets Syst 59:125–166
Yang B, Hu BQ (2018) Matrix representations and interdependency on \(L\)-fuzzy covering-based approximation operators. Int J Approx Reason 96:57–77
Yao YQ, Mi JS, Li ZJ (2014) A novel variable precision (\(\theta\), \(\sigma\))-fuzzy rough set model based on fuzzy granules. Fuzzy Sets Syst 236:58–72
Yao YY (2018) Three-way decision and granular computing. Int J Approx Reason 103:107–123
Yao YY, Yao BX (2012) Covering based rough set approximations. Inform. Sci. 200:91–107
Zadeh LA (1965) Fuzzy sets, Inform. Control 8:338–353
Zhan JM, Jiang HB, Yao YY (2020) Covering-based variable precision fuzzy rough sets with PROMETHEE-EDAS methods. Inform Sci 538:314–336
Zhang C, Li DY, Liang JY (2020) Interval-valued hesitant fuzzy multi-granularity three-way decisions in consensus processes with applications to multi-attribute group decision making. Inform Sci 511:192–211
Zhang K, Zhan JM, Wang XZ (2020) TOPSIS-WAA method based on a covering-based fuzzy rough set: an application to rating problem. Inform Sci 539:397–421
Zhang K, Zhan JM, Wu WZ (2020) On multi-criteria decision-making method based on a fuzzy rough set model with fuzzy \(\alpha\)-neighborhoods. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2020.3001670
Zhao SY, Tsang ECC, Chen DG (2009) The model of fuzzy variable percision rough sets. IEEE Trans Fuzzy Syst 17:451–467
Zhao XR, Hu BQ (2015) Fuzzy variable precision rough sets based on residuated lattices. Int J Gen Syst 44:743–765
Ziarko W (1993) Variable precision rough set model. J Comput Syst Sci 46:39–59
Acknowledgements
The authors are extremely grateful to the editors and three reviewers for their valuable comments and helpful suggestions which helped to improve the presentation of this paper. This research is partially supported by NNSFC (11961025; 61866011).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declared that they have no conflicts of interest to this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jiang, H., Zhan, J. & Chen, D. Covering-based variable precision L-fuzzy rough sets based on residuated lattices and corresponding applications. Int. J. Mach. Learn. & Cyber. 12, 2407–2429 (2021). https://doi.org/10.1007/s13042-021-01320-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-021-01320-w