Global exponential stability of uncertain memristor-based recurrent neural networks with mixed time delays | International Journal of Machine Learning and Cybernetics Skip to main content
Springer Nature Link
Log in

Global exponential stability of uncertain memristor-based recurrent neural networks with mixed time delays

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

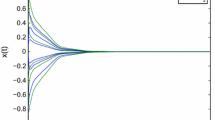
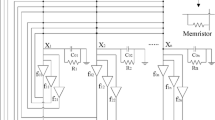
The global exponential stability of the equilibrium point for uncertain memristor-based recurrent neural networks is studied in this paper. The memristor-based recurrent neural networks considered in this paper are based on a realistic memristor model, and can be considered as the extension of some existing memristor-based recurrent neural networks. By virtue of homomorphic theory, it is proved that the uncertain memristor-based recurrent neural networks have a unique equilibrium point under some mild assumptions. Moreover, the unique equilibrium point is proved to be globally exponentially stable by constructing a suitable Lyapunov functional. Finally, the obtained results are applied to determine the dynamical behaviors and circuit design of the memristor-based recurrent neural networks by some numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Chua LO (1971) Memristor-the missing circuit element. IEEE Trans Circuit Theory 18:507–519

    Article  Google Scholar 

  2. Strukov DB, Snider GS, Stewart DR, Williams RS (2008) The missing memristor found. Nature 453:80–83

    Article  Google Scholar 

  3. Lu W (2012) Memristors: going active. Nat Mater 12(2):93–94

    Article  Google Scholar 

  4. Thomas A (2013) Memristor-based neural networks. J Phys D Appl Phys 46:093001/1–093001/12

    Google Scholar 

  5. Qin S, Bian W, Xue X (2013) A new one-layer recurrent neural network for nonsmooth pseudoconvex optimization. Neurocomputing 120:655–662

    Article  Google Scholar 

  6. Qin S, Xue X (2015) A two-layer recurrent neural network for nonsmooth convex optimization problems. IEEE Trans Neural Netw Learn Syst 26(6):1149–1160

    Article  MathSciNet  Google Scholar 

  7. Qin S, Fan D, Wu G, Zhao L (2015) Neural network for constrained nonsmooth optimization using Tikhonov regularization. Neural Netw 63:272–281

    Article  MATH  Google Scholar 

  8. Zhu Q, Cao J, Rakkiyappan R (2015) Exponential input-to-state stability of stochastic Cohen–Grossberg neural networks with mixed delays. Nonlinear Dyn 2(79):1085–1098

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhu Q, Cao J (2014) Mean-square exponential input-to-state stability of stochastic delayed neural networks. Neurocomputing 131:157–163

    Article  Google Scholar 

  10. Zhu Q, Cao J (2012) Stability analysis of Markovian jump stochastic BAM neural networks with impulse control and mixed time delays. IEEE Trans Neural Netw Learn Syst 23(3):467–479

    Article  MathSciNet  Google Scholar 

  11. Zhu Q, Cao J (2012) Stability of Markovian jump neural networks with impulse control and time varying delays. Nonlinear Anal Real World Appl 13(5):2259–2270

    Article  MathSciNet  MATH  Google Scholar 

  12. Xie W, Zhu Q (2015) Mean square exponential stability of stochastic fuzzy delayed Cohen–Grossberg neural networks with expectations in the coefficients. Neurocomputing 166:133–139

    Article  Google Scholar 

  13. Ali MS, Gunasekaran N, Zhu Q (2017) State estimation of T–S fuzzy delayed neural networks with Markovian jumping parameters using sampled-data control. Fuzzy Sets Syst 306:87–104

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu L, Zhu Q (2015) Almost sure exponential stability of numerical solutions to stochastic delay Hopfield neural networks. Appl Math Comput 266:698–712

    MathSciNet  MATH  Google Scholar 

  15. Zhu Q, Cao J, Hayat T, Alsaadi F (2015) Robust stability of Markovian jump stochastic neural networks with time delays in the leakage terms. Neural Process Lett 41(1):1–27

    Article  Google Scholar 

  16. Qin S, Xue X, Wang P (2012) Global exponential stability of almost periodic solution of delayed neural networks with discontinuous activations. Inf Sci 220:367–378

    Article  MathSciNet  MATH  Google Scholar 

  17. Qin S, Fan D, Yan M, Liu Q (2014) Global robust exponential stability for interval delayed neural networks with possibly unbounded activation functions. Neural Process Lett 40(1):35–50

    Article  Google Scholar 

  18. Qin S, Xu J, Shi X (2014) Convergence analysis for second-order interval Cohen–Grossberg neural networks. Commun Nonlinear Sci Numer Simul 19(8):2747–2757

    Article  MathSciNet  Google Scholar 

  19. Zhou C, Zhang W, Yang X, Xu C, Feng J (2017) Finite-time synchronization of complex-valued neural networks with mixed delays and uncertain perturbations. Neural Process Lett 46(1):271–291

    Article  Google Scholar 

  20. Yang X, Feng Z, Feng J, Cao J (2016) Synchronization of discrete-time neural networks with delays and Markov jump topologies based on tracker information. Neural Netw 85(C):157–164

    Google Scholar 

  21. Anthes G (2011) Memristors: pass or fail? Commun ACM 54(3):22–24

    Article  MathSciNet  Google Scholar 

  22. Qin S, Wang J, Xue X (2015) Convergence and attractivity of memristor-based cellular neural networks with time delays. Neural Netw 63:223–233

    Article  MATH  Google Scholar 

  23. Wang L, Duan M, Duan S (2013) Memristive perceptron for combinational logic classification. Math Probl Eng 4:211–244

    MathSciNet  MATH  Google Scholar 

  24. Hu J, Wang J (2010) Global uniform asymptotic stability of memristor-based recurrent neural networks with time delays. IEEE Congress Comput Intell Barc Spain 2010:2127–2134

    Google Scholar 

  25. Wu A, Zeng Z, Zhu X, Zhang J (2011) Exponential synchronization of memristor-based recurrent neural networks with time delays. Neurocomputing 74(17):3043–3050

    Article  Google Scholar 

  26. Wu A, Zeng Z (2012) Exponential stabilization of memristive neural networks with time delays. IEEE Trans Neural Netw Learn Syst 23:1919–1929

    Article  Google Scholar 

  27. Wu H, Zhang X, Li R, Yao R (2015) Adaptive anti-synchronization and anti-synchronization for memristive neural networks with mixed time delays and reaction-diffusion terms. Neurocomputing 168:726–740

    Article  Google Scholar 

  28. Wu A, Zeng Z (2014) Lagrange stability of memristive neural networks with discrete and distributed delays. IEEE Trans Neural Netw Learn Syst 25(4):690–703

    Article  Google Scholar 

  29. Yang S, Guo Z, Wang J (2015) Robust synchronization of multiple memristive neural networks with uncertain parameters via nonlinear coupling. IEEE Trans Syst Man Cybern Syst 45(7):1077–1086

    Article  Google Scholar 

  30. Wu A, Zeng Z (2013) Anti-synchronization control of a class of memristive recurrent neural networks. Commun Nonlinear Sci Numer Simul 18:373–385

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang G, Shen Y (2014) Exponential synchronization of coupled memristive neural networks with time delays. Neural Comput Appl 24(6):1421–1430

    Article  Google Scholar 

  32. Wen S, Zeng Z, Huang T (2013) Dynamic behaviors of memristor-based delayed recurrent networks. Neural Comput Appl 23(3–4):815–821

    Article  Google Scholar 

  33. Guo Z, Wang J, Y Z (2014) Attractivity analysis of memristor-based cellular neural networks with time-varying delays. IEEE Trans Neural Netw Learn Syst 25(4):704–717

    Article  Google Scholar 

  34. Wen S, Bao G, Zeng Z, Chen Y, Huang T (2013) Global exponential synchronization of memristor-based recurrent neural networks with time-varying delays. Neural Netw 48:195–203

    Article  MATH  Google Scholar 

  35. Chen L, Wu R, Cao J, Liu J-B (2015) Stability and synchronization of memristor-based fractional-order delayed neural networks. Neural Netw 71:37–44

    Article  MATH  Google Scholar 

  36. Li JN, Li LS (2015) Mean-square exponential stability for stochastic discrete-time recurrent neural networks with mixed time delays. Neurocomputing 151:790–797

    Article  Google Scholar 

  37. Li JN et al (2016) Exponential synchronization of discrete-time mixed delay neural networks with actuator constraints and stochastic missing data. Neurocomputing 207(2016):700–707

    Article  Google Scholar 

  38. Arik S (2014) New criteria for global robust stability of delayed neural networks with norm-bounded uncertainties. IEEE Trans Neural Netw Learn Syst 25(25):1045–1052

    Google Scholar 

  39. Jarina Banu L, Balasubramaniam P (2016) Robust stability analysis for discrete-time neural networks with time-varying leakage delays and random parameter uncertainties. Neurocomputing 179:126–134

    Article  Google Scholar 

  40. Wang X, Li C, Huang T (2014) Delay-dependent robust stability and stabilization of uncertain memristive delay neural networks. Neurocomputing 140:155–161

    Article  Google Scholar 

  41. Yang S, Guo Z, Wang J (2015) Robust synchronization of multiple memristive neural networks with uncertain parameters via nonlinear coupling. IEEE Trans Syst Man Cybern Syst 45(7):1077–1086

    Article  Google Scholar 

  42. Faydasicok O, Arik S (2012) Robust stability analysis of a class of neural networks with discrete time delays. Neural Netw 29–30(5):1407–1414

    MATH  Google Scholar 

  43. Qin S, Cheng Q, Chen G (2016) Global exponential stability of uncertain neural networks with discontinuous Lurie-type activation and mixed delays. Neurocomputing 198(C):12–19

    Article  Google Scholar 

  44. Feng J, Ma Q, Qin S (2017) Exponential stability of periodic solution for impulsive memristor-based Cohen–Grossberg neural networks with mixed delays. Int J Pattern Recogn Artif Intell 31(27):1750022

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant (11201100, 11401142, 61403101), and Heilongjiang Province Science and Technology Agency Funds of China (A201213).

Author information

Authors and Affiliations

  1. Department of Electronic Science and Technology, Harbin University of Science and Technology, Harbin, 150080, People’s Republic of China

    Jianmin Wang

  2. Department of Applied Mathematics, Harbin University of Science and Technology, Harbin, 150080, People’s Republic of China

    Fengqiu Liu

  3. Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, People’s Republic of China

    Sitian Qin

Authors
  1. Jianmin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fengqiu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sitian Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianmin Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., Liu, F. & Qin, S. Global exponential stability of uncertain memristor-based recurrent neural networks with mixed time delays. Int. J. Mach. Learn. & Cyber. 10, 743–755 (2019). https://doi.org/10.1007/s13042-017-0759-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-017-0759-4

Keywords

Search

Navigation