Analysis of the strategy of competing retailers in hiring a purchasing agent under a price discount contract

Abstract

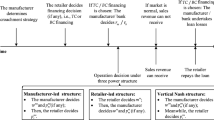
Currently, an increasing number of retailers are hiring purchasing agents to source products from upstream manufacturers instead of sourcing directly themselves. The retailers’ choices of purchasing agents are influenced not only by the agents’efficiencies and costs, but also by the competitors’ purchasing strategies. On this basis, this study establishes a Nash game model to investigate two competing retailers’ sourcing strategies from a common manufacturer: purchasing themselves with a base wholesale price or purchasing through an agent with a lower wholesale price. We find that, for the retailers, when both retailers choose a purchasing agent, it is not always superior to the case in which neither of them does; this completely depends on the agent’s efficiency and has nothing to do with the agency fee. Second, regardless of the competitor’s strategy, the retailer always chooses to hire an agent if the efficiency of the agent is relatively high and the cost is sufficiently low, which can yield a lower wholesale price at an acceptable agency fee. Finally, we verify that a Nash equilibrium can be achieved only when the two retailers have the same purchasing strategy, i.e., neither of the retailers hires a purchasing agent or both of them do, and the case in which only one retailer hires an agent is never an equilibrium.

Appendix 1

Proof of Lemma 4

From Lemmas 1 and 3, we have $\Pi _{\text {R}_1}^{\text {AA}}-\Pi _{\text {R}_1}^{\text {NN}}=-\frac{\varphi (-w^2+\mu )}{-9\varphi w^2+9\mu }$. From $\Pi _{\text {R}_1}^{\text {AA}}-\Pi _{\text {R}_1}^{\text {NN}} > 0$, we obtain $\mu <w^2$, otherwise $\Pi _{\text {R}_1}^{\text {AA}}-\Pi _{\text {R}_1}^{\text {NN}} < 0$. This completes the proof. $\square$

Proof of Lemma 5

From Lemmas 1 and 2, we obtain $\Pi _{\text {R}_1}^{\text {AN}} - \Pi _{\text {R}_1}^{\text {NN}} = \frac{\varphi Q}{9(4\varphi w^2-3\mu )^2}$, where $Q = ( - 16w^4 + 9\mu w^2)\varphi + 15\mu w^2 - 9\mu ^2$. When $\mu > \frac{16w^2}{9}$, $Q < 0$, and thus $\Pi _{\text {R}_1}^{\text {AN}} - \Pi _{\text {R}_1}^{\text {NN}} < 0$; When $\frac{16w^2}{9}> \mu > \frac{15w^2}{9}$, $Q<0$ and thus $\Pi _{\text {R}_1}^{\text {AN}} - \Pi _{\text {R}_1}^{\text {NN}} < 0$; When $\frac{15w^2}{9} > \mu$, let $Q=0$ and we obtain $\phi _1 = \frac{(9\mu -15w^2)\mu }{(9\mu -16w^2)w^2}$. Therefore, we have $Q < 0$ and thus $\Pi _{\text {R}_1}^{\text {AN}} - \Pi _{\text {R}_1}^{\text {NN}} < 0$ if $\phi > \phi _1$, otherwise $\Pi _{\text {R}_1}^{\text {AN}} - \Pi _{\text {R}_1}^{\text {NN}} > 0$. $\square$

Proof of Lemma 6

From Lemmas 2 and 3, we obtain $\Pi _{\text {R}_1}^{\text {AA}} - \Pi _{\text {R}_2}^{\text {AN}} = \frac{M}{9(4\varphi w^2-3\mu )^2(\varphi w^2 - \mu )}$, where $M = (-36w^6 + 16\mu w^4)\varphi ^2 + (56\mu w^4 - 24\mu ^2 w^2)\varphi - 21w^2\mu ^2 + 9\mu ^3$. When $\mu > \frac{7w^2}{3}$, $M > 0$ and thus $\Pi _{\text {R}_1}^{\text {AA}} - \Pi _{\text {R}_2}^{\text {AN}} < 0$; When $\frac{7w^2}{3}> \mu > \frac{9w^2}{4}$, let $M = 0$ and we obtain $\phi _2 = \frac{(-14w^2+6\mu +\root 2 \of {7W^4-3\mu w^2})\mu }{2(4\mu -9w^2)w^2}$. Therefore, we have $M > 0$ and thus $\Pi _{\text {R}_1}^{\text {AA}} - \Pi _{\text {R}_2}^{\text {AN}} < 0$ if $\phi > \phi _2$, otherwise $\Pi _{\text {R}_1}^{\text {AA}} - \Pi _{\text {R}_2}^{\text {AN}} > 0$; When $\frac{9w^2}{4} > \mu$, $M > 0$ and thus $\Pi _{\text {R}_1}^{\text {AA}} - \Pi _{\text {R}_2}^{\text {AN}} < 0$. $\square$

Proof of Proposition 2

$\Pi _\mathrm{{P}}^{{\text {AA}}} - \Pi _\mathrm{{P}}^{{\text {AN}}}$ $= -\frac{(a-w)^2\mu \varphi (101\varphi ^3 w^6 - 184\mu \varphi ^2 w^4 + 105\mu ^2\varphi w^2 - 18\mu ^3)}{(288(\varphi w^2-\mu )^2 (\varphi w^2-\frac{3}{4}\mu )^2)}$. Let $f(\mu ) =-( 101\varphi ^3 w^6 - 184\mu \varphi ^2 w^4 + 105\mu ^2\varphi w^2 - 18\mu ^3)$, then $f(\mu ) < 0$ in $[2\phi w^2, \frac{23}{9}\phi w^2]$ and $f(\mu ) > 0$ in $[\frac{23}{9}\phi w^2,+\infty ]$. Hence, the function f(u) must have a root $\mu _0$ in $[2\phi w^2, +\infty ]$ . From the above analysis we can obtain that $\Pi _\mathrm{{P}}^{{\text {AA}}} - \Pi _\mathrm{{P}}^{{\text {AN}}}<0$ if $\mu <\mu _0$ and $\Pi _\mathrm{{P}}^{{\text {AA}}} - \Pi _\mathrm{{P}}^{{\text {AN}}}>0$ if $\mu >\mu _0$. $\square$