PySP: modeling and solving stochastic programs in Python | Mathematical Programming Computation Skip to main content
Springer Nature Link
Log in

PySP: modeling and solving stochastic programs in Python

  • Full Length Paper
  • Published:
Mathematical Programming Computation Aims and scope Submit manuscript

Abstract

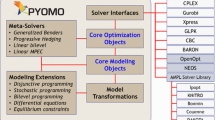
Although stochastic programming is a powerful tool for modeling decision-making under uncertainty, various impediments have historically prevented its wide-spread use. One factor involves the ability of non-specialists to easily express stochastic programming problems as extensions of their deterministic counterparts, which are typically formulated first. A second factor relates to the difficulty of solving stochastic programming models, particularly in the mixed-integer, non-linear, and/or multi-stage cases. Intricate, configurable, and parallel decomposition strategies are frequently required to achieve tractable run-times on large-scale problems. We simultaneously address both of these factors in our PySP software package, which is part of the Coopr open-source Python repository for optimization; the latter is distributed as part of IBM’s COIN-OR repository. To formulate a stochastic program in PySP, the user specifies both the deterministic base model (supporting linear, non-linear, and mixed-integer components) and the scenario tree model (defining the problem stages and the nature of uncertain parameters) in the Pyomo open-source algebraic modeling language. Given these two models, PySP provides two paths for solution of the corresponding stochastic program. The first alternative involves passing an extensive form to a standard deterministic solver. For more complex stochastic programs, we provide an implementation of Rockafellar and Wets’ Progressive Hedging algorithm. Our particular focus is on the use of Progressive Hedging as an effective heuristic for obtaining approximate solutions to multi-stage stochastic programs. By leveraging the combination of a high-level programming language (Python) and the embedding of the base deterministic model in that language (Pyomo), we are able to provide completely generic and highly configurable solver implementations. PySP has been used by a number of research groups, including our own, to rapidly prototype and solve difficult stochastic programming problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. AIMMS: Optimization software for operations research applications. http://www.aimms.com/operations-research/mathematical-programming/stochastic-programming, July (2010)

  2. Alonso-Ayuso A., Escudero L.F., Ortuño M.T.: BFC, a branch-and-fix coordination algorithmic framework for solving some types of stochastic pure and mixed 0-1 programs. Eur. J. Oper. Res. 151(3), 503–519 (2003)

    Article  MATH  Google Scholar 

  3. AMPL: A modeling language for mathematical programming. http://www.ampl.com, July (2010)

  4. Badilla, F.: Problema de Planificación Forestal Estocástico Resuelto a Traves del Algoritmo Progressive Hedging. PhD thesis, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Santiago, Chile (2010)

  5. Bertsekas D.P.: Constrained Optimization and Lagrange Multiplier Methods. Athena Scientific, Massachusetts (1996)

    Google Scholar 

  6. Birge J.R.: Decomposition and partitioning methods for multistage stochastic linear programs. Oper. Res. 33, 989–1007 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  7. Birge J.R., Dempster M.A., Gassmann H.I., Gunn E.A., King A.J., Wallace S.W.: A standard input format for multiperiod stochastic linear program. COAL (Math. Prog. Soc. Commun. Algorithms) Newsletter 17, 1–19 (1987)

    Google Scholar 

  8. Birge J.R., Louveaux F.: Introduction to Stochastic Programming. Springer, Berlin (1997)

    MATH  Google Scholar 

  9. Carøe C.C., Schultz R.: Dual decomposition in stochastic integer programming. Oper. Res. Lett. 24(1–2), 37–45 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chen D.-S., Batson R.G., Dang Y.: Applied Integer Programming. Wiley, New York (2010)

    MATH  Google Scholar 

  11. COIN-OR: COmputational INfrastructure for Operations Research. http://www.coin-or.org, July (2010)

  12. CPLEX: http://www.cplex.com, July (2010)

  13. Crainic, T.G., Fu, X., Gendreau, M., Rei, W., Wallace, S.W.: Progressive hedging-based meta-heuristics for stochastic network design. Technical report CIRRELT-2009-03, University of Montreal CIRRELT, January (2009)

  14. Fan Y., Liu C.: Solving stochastic transportation network protection problems using the progressive hedging-based method. Netw. Spatial Econ. 10(2), 193–208 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  15. FLOPCPP: Flopc++: Formulation of linear optimization problems in C++. http://www.projects.coin-or.org/FlopC++, August (2010)

  16. Fourer R., Gay D.M., Kernighan B.W.: AMPL: a mathematical programming language. Manage. Sci. 36, 519–554 (1990)

    Article  MATH  Google Scholar 

  17. Fourer R., Lopes L.: A management system for decompositions in stochastic programming. Ann. Oper. Res. 142, 99–118 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fourer R., Lopes L.: StAMPL: a filtration-oriented modeling tool for multistage recourse problems. INFORMS J. Comput. 21(2), 242–256 (2009)

    Article  MathSciNet  Google Scholar 

  19. Fourer R., Ma J., Martin K.: OSiL: an instance language for optimization. Comput. Optim. Appl. 45(1), 181–203 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  20. FrontLine: Frontline solvers: developers of the Excel solver. http://www.solver.com, July (2011)

  21. GAMS: The General Algebraic Modeling System. http://www.gams.com, July (2010)

  22. Gassmann H.I.: MSLiP: a computer code for the multistage stochastic linear programming problem. Math. Program. 47, 407–423 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  23. Gassmann H.I., Ireland A.M.: On the formulation of stochastic linear programs using algebraic modeling languages. Ann. Oper. Res. 64, 83–112 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  24. Gassmann H.I., Schweitzer E.: A comprehensive input format for stochastic linear programs. Ann. Oper. Res. 104, 89–125 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  25. GUROBI: Gurobi optimization. http://www.gurobi.com, July (2010)

  26. Hart W.E., Laird C.D., Watson J.P., Woodruff D.L.: Pyomo: Optimization Modeling in Python. Springer, Berlin (2012)

    Book  MATH  Google Scholar 

  27. Hart, W.E., Siirola, J.D.: The PyUtilib component architecture. Technical report, Sandia National Laboratories (2010)

  28. Hart W.E., Watson J.P., Woodruff D.L.: Python optimization modeling objects (Pyomo). Math. Program. Comput. 3, 219–260 (2011)

    Article  MathSciNet  Google Scholar 

  29. Helgason T., Wallace S.W.: Approximate scenario solutions in the progressive hedging algorithm: a numerical study. Ann. Oper. Res. 31(1–4), 425–444 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  30. Huang, Y.: Sustainable Infrastructure System Modeling under Uncertainties and Dynamics. PhD thesis, Department of Civil and Environmental Engineering, University of California, Davis (2010)

  31. Hvattum L.M., Løkketangen A.: Using scenario trees and progressive hedging for stochastic inventory routing problems. J. Heurist. 15(6), 527–557 (2009)

    Article  MATH  Google Scholar 

  32. Jorjani S., Scott C.H., Woodruff D.L.: Selection of an optimal subset of sizes. Int. J. Prod. Res. 37(16), 3697–3710 (1999)

    Article  MATH  Google Scholar 

  33. Kall, P., Mayer, J.: Building and solving stochastic linear programming models with SLP-IOR. In: Wallace, S.W., Ziemba, W.T. (eds.) Applications of Stochastic Programming, pp. 79–93. MPS-SIAM (2005)

  34. Kall P., Mayer J.: Stochastic Linear Programming: Models, Theory, and Computation. Springer, Berlin (2005)

    MATH  Google Scholar 

  35. Karabuk, S.: An open source algebraic modeling and programming software. Technical report, University of Oklahoma, School of Industrial Engineering, Norman (2005)

  36. Karabuk S.: Extending algebraic modeling languages to support algorithm development for solving stochastic programming models. IMA J. Manage. Math. 19, 325–345 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  37. Karabuk S., Grant F.H.: A common medium for programming operations-research models. IEEE Softw. 24(5), 39–47 (2007)

    Article  Google Scholar 

  38. LINDO: LINDO systems, August (2010)

  39. Listes O., Dekker R.: A scenario aggregation based approach for determining a robust airline fleet composition. Transport. Sci. 39, 367–382 (2005)

    Article  Google Scholar 

  40. Løkketangen A., Woodruff D.L.: Progressive hedging and tabu search applied to mixed integer (0,1) multistage stochastic programming. J. Heurist. 2, 111–128 (1996)

    Article  Google Scholar 

  41. Maximal Software: http://www.maximal-usa.com/maximal/news/stochastic.html, July (2010)

  42. Parija G.R., Ahmed S., King A.J.: On bridging the gap between stochastic integer programming and mip solver technologies. INFORMS J. Comput. 16, 73–83 (2004)

    Article  MathSciNet  Google Scholar 

  43. PYRO: Python remote objects. http://pyro.sourceforge.net, July (2009)

  44. Python: Python programming language—official website. http://python.org, July (2010)

  45. Dive Into Python: http://diveintopython.org/power_of_introspection/index.html, July (2010)

  46. Rockafellar R.T., Wets R.J.-B.: Scenarios and policy aggregation in optimization under uncertainty. Math. Oper. Res. 16(1), 119–147 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  47. Schultz R., Tiedemann S.: Conditional value-at-risk in stochastic programs with mixed-integer recourse. Math. Program. 105(2–3), 365–386 (2005)

    MathSciNet  Google Scholar 

  48. Shapiro, A., Dentcheva, D., Ruszczynski, A.: Lectures on stochastic programming: modeling and theory. Society for Industrial and Applied Mathematics (SIAM) (2009)

  49. SMI: SMI. http://www.projects.coin-org.org/Smi, August (2010)

  50. SUTIL: SUTIL—a stochastic programming utility library. http://www.coral.ie.lehigh.edu/~sutil, July (2011)

  51. Thénié J., van Delft Ch., Vial J.-Ph.: Automatic formulation of stochastic programs via an algebraic modeling language. Comput. Manage. Sci. 4(1), 17–40 (2007)

    Article  MATH  Google Scholar 

  52. Valente C., Mitra G., Sadki M., Fourer R.: Extending algebraic modelling languages for stochastic programming. INFORMS Journal On Computing 21(1), 107–122 (2009)

    Article  MathSciNet  Google Scholar 

  53. Valente, P., Mitra, G., Poojari, C.A.: A stochastic programming integrated environment. In: Wallace, S.W., Ziemba, W.T. (eds.) Applications of Stochastic Programming, pp. 115–136. MPS-SIAM (2005)

  54. Van Slyke R.M., Wets R.J.-B.: L-shaped linear programs with applications to optimal control and stochastic programming. SIAM J. Appl. Math. 17, 638–663 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  55. Wallace, S.W., Ziemba, W.T. (eds.): Applications of Stochastic Programming. Society for Industrial and Applied Mathematics (SIAM) and the Mathematical Programming Society (MPS) (2005)

  56. Watson J.P., Woodruff D.L.: Progressive hedging innovations for a class of stochastic mixed-integer resource allocation problems. Comput. Manage. Sci. 8(4), 355–370 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  57. Woodruff D.L., Zemel E.: Hashing vectors for tabu search. Ann. Oper. Res. 41(2), 123–137 (1993)

    Article  MATH  Google Scholar 

  58. Word, D.P., Burke, D.A., Iamsirithaworn, D.S., Laird, C.D.: A nonlinear programming approach for estimation of transmission parameters in childhood infectious disease using a continuous time model. J. R. Soc. Interface (Under Review)

  59. Xpress-Mosel. http://www.dashopt.com/home/products/products_sp.html, July (2010, to appear)

  60. XpressMP: FICO express optimization suite. http://www.fico.com/en/products/DMTools/pages/FICO-Xpress-Optimization-Suite.aspx, July (2010)

Download references

Author information

Authors and Affiliations

  1. Discrete Math and Complex Systems Department, Sandia National Laboratories, PO Box 5800, MS 1326, Albuquerque, NM, 87185-1326, USA

    Jean-Paul Watson

  2. Graduate School of Management, University of California Davis, Davis, CA, 95616-8609, USA

    David L. Woodruff

  3. Computer Science and Informatics Department, Sandia National Laboratories, PO Box 5800, MS 1327, Albuquerque, NM, 87185-1327, USA

    William E. Hart

Authors
  1. Jean-Paul Watson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David L. Woodruff
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. William E. Hart
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jean-Paul Watson.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Watson, JP., Woodruff, D.L. & Hart, W.E. PySP: modeling and solving stochastic programs in Python. Math. Prog. Comp. 4, 109–149 (2012). https://doi.org/10.1007/s12532-012-0036-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12532-012-0036-1

Mathematics Subject Classification (2000)

Search

Navigation