An efficient numerical method based on Chelyshkov operation matrix for solving a type of time-space fractional reaction diffusion equation | Journal of Applied Mathematics and Computing Skip to main content
Springer Nature Link
Log in

An efficient numerical method based on Chelyshkov operation matrix for solving a type of time-space fractional reaction diffusion equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

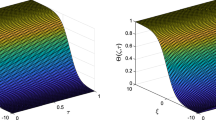
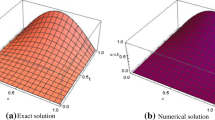
In this article, a numerical method based on Chelyshkov operation matrix is built to investigate a time-space fractional reaction diffusion model. First of all, we transform the solution of time-space fractional reaction diffusion equation into the solution of a linear system by using operational matrix method. Next, in order to validate the accuracy of this proposed method, error analysis is performed. At last, three excellent numerical examples are also provided to demonstrate the effectiveness and feasibility of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Hilfer, R., Luchko, Y., Tomovski, Z.: Operational method for the solution of fractional differential equations with generalized Riemann-Liouville fractional derivatives. J. Math. Anal. Appl. 12, 299–318 (2009)

    MathSciNet  Google Scholar 

  2. Wang, G.: Monotone iterative technique for boundary value problems of a nonlinear fractional differential equation with deviating arguments. J. Comput. Appl. Math. 236, 2425–2430 (2012)

  3. Zhang, L., Ahmad, B., Wang, G., et al.: Nonlinear fractional integro-differential equations on unbounded domains in a Banach space. J. Comput. Appl. Math. 249, 51–56 (2013)

    Article  MathSciNet  Google Scholar 

  4. Jafari, H., Jassim, H.K., Baleanu, D., et al.: On the approximate solutions for a system of coupled Korteweg-de Vries equations with local fractional derivative. Fractals 29, 2140012 (2021)

    Article  ADS  Google Scholar 

  5. Wang, G., Ren, X., Zhang, L., et al.: Explicit iteration and unique positive solution for a Caputo-Hadamard fractional turbulent flow model. IEEE Access 7, 109833–109839 (2019)

    Article  Google Scholar 

  6. Cruz-Duarte, J.M., Rosales-Garcia, J., Correa-Cely, C.R., et al.: A closed form expression for the Gaussian-based Caputo-Fabrizio fractional derivative for signal processing applications. Commun. Nonlinear Sci. Numer. Simul. 61, 138–148 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  7. Shitikova, M.V.: Fractional operator viscoelastic models in dynamic problems of mechanics of solids: A review, Mechanics of Solids, 1-33 (2021)

  8. Zhou, F., Wang, L., Liu, Z., et al.: A viscoelastic-viscoplastic mechanical model of time-dependent materials based on variable-order fractional derivative. Mech. Time-Depend. Mater. 26, 699–717 (2022)

    Article  ADS  Google Scholar 

  9. Al-Raeei, M.: Applying fractional quantum mechanics to systems with electrical screening effects. Chaos Solitons Fractals 150, 111209 (2021)

    Article  MathSciNet  Google Scholar 

  10. Zhang, Z., Zeb, A., Egbelowo, O.F., et al.: Dynamics of a fractional order mathematical model for COVID-19 epidemic. Adv. Differ. Equ. 2020, 1–16 (2020)

    Article  MathSciNet  CAS  PubMed  PubMed Central  Google Scholar 

  11. Veeresha, P., Ilhan, E., Prakasha, D.G., et al.: A new numerical investigation of fractional order susceptible-infected-recovered epidemic model of childhood disease. Alex. Eng. J. 61, 747–1756 (2022)

    Article  Google Scholar 

  12. Hattaf, K.: On the stability and numerical scheme of fractional differential equations with application to biology. Computation 10, 97 (2022)

    Article  Google Scholar 

  13. Ikram, M.D., Imran, M.A., Chu, Y.M., et al.: MHD flow of a Newtonian fluid in symmetric channel with ABC fractional model containing hybrid nanoparticles. Combinat. Chem. High Throughput Screen. 25, 1087–1102 (2022)

    Article  CAS  Google Scholar 

  14. Chu, Y.M., Rashid, S., Karim, S. et al.: New configurations of the fuzzy fractional differential Boussinesq model with application in ocean engineering and their analysis in statistical theory. CMES-Comput. Model. Eng. Sci. 137 (2023)

  15. Chu, Y.M., Khan, M.F., Ullah, S., et al.: Mathematical assessment of a fractional-order vector-host disease model with the Caputo-Fabrizio derivative. Math. Methods Appl. Sci. 46, 232–247 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  16. Ahmad, I., Ahmad, H., Thounthong, P., et al.: Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry 12, 1195 (2020)

    Article  ADS  Google Scholar 

  17. Chu, Y.M., Bani Hani, E.H., El-Zahar, E.R. et al.: Combination of Shehu decomposition and variational iteration transform methods for solving fractional third order dispersive partial differential equations. Numer. Methods Partial Differ. Equ. (2021)

  18. Liu, W., Huang, J., Long, X.: Coupled nonlinear advection-diffusion-reaction system for prevention of groundwater contamination by modified upwind finite volume element method. Comput. Math. Appl. 69, 477–493 (2015)

    Article  MathSciNet  Google Scholar 

  19. Shi, X.C., Cai, W.Q., Meng, Y.F.: Study on the model of contaminant ions reaction and diffusion near wellbore. Thermal Sci. 19(suppl 1), 157-162 (2015)

  20. Park, J., Hong, G.: Simulation on the permeability evaluation of a hybrid liner for the prevention of contaminant diffusion in soils contaminated with total petroleum hydrocarbon. Int. J. Environ. Res. Public Health 19, 13710 (2022)

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Wang, X., Wang, B., Meyerson, M., et al.: A phase-field model integrating reaction-diffusion kinetics and elasto-plastic deformation with application to lithiated selenium-doped germanium electrodes. Int. J. Mech. Sci. 144, 158–171 (2018)

    Article  Google Scholar 

  22. Mozafarifard, M., Toghraie, D.: Time-fractional subdiffusion model for thin metal films under femtosecond laser pulses based on Caputo fractional derivative to examine anomalous diffusion process. Int. J. Heat Mass Transf. 153, 119592 (2020)

    Article  CAS  Google Scholar 

  23. Manimaran, J., Shangerganesh, L.: Existence and uniqueness of time-fractional nonlocal diffusion systems modelling an epidemic disease. Indian J. Indus. Appl. Math. 193-207 (2020)

  24. Jayathunga, Y., Bock, W.: An ADI scheme for two-sided fractional reaction-diffusion equations and applications to an epidemic model. Authorea Preprints. (2020)

  25. Graham, A.: Kronecker products and matrix calculus with applications. Courier Dover Publications, New York (2018)

    Google Scholar 

  26. Miller, K.S., Ross, B.: An introduction to the fractional calculus and fractional differential equations, New York, (1993)

  27. Chelyshkov, V.S.: Alternative orthogonal polynomials and quadratures. Electron. Trans. Numer. Anal. 25, 17–26 (2016)

    MathSciNet  Google Scholar 

  28. Kumar, D., Baleanu, D.: Fractional calculus and its applications in physics. Front. Phys. 7, 81 (2019)

    Article  Google Scholar 

  29. Chen, Y., Wu, Y., Cui, Y., et al.: Wavelet method for a class of fractional convection-diffusion equation with variable coefficients. J. Comput. Sci. 1, 146–149 (2010)

    Article  Google Scholar 

  30. Kargar, Z., Saeedi, H.: B-spline wavelet operational method for numerical solution of time-space fractional partial differential equations. Int. J. Wavelets Multiresolut. Inf. Process. 15, 1750034 (2017)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Computer Science, Shanxi Normal University, Taiyuan, 030031, Shanxi, China

    Lihong Zhang, Keke Lu & Guotao Wang

Authors
  1. Lihong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Keke Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guotao Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guotao Wang.

Ethics declarations

Conflict of interest

Not Applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supported by NNSFC(No. 12001344), NSF of Shanxi Province, China (No. 20210302123339) and the Graduate Education and Teaching Innovation Project of Shanxi, China (No. 2022YJJG124).

All authors contributed equally to this work.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, L., Lu, K. & Wang, G. An efficient numerical method based on Chelyshkov operation matrix for solving a type of time-space fractional reaction diffusion equation. J. Appl. Math. Comput. 70, 351–374 (2024). https://doi.org/10.1007/s12190-023-01971-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-023-01971-8

Keywords

Mathematics Subject Classification

Search

Navigation