A new development of sixth order accurate compact scheme for the Helmholtz equation | Journal of Applied Mathematics and Computing Skip to main content
Springer Nature Link
Log in

A new development of sixth order accurate compact scheme for the Helmholtz equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

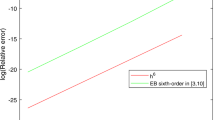
A standard sixth order compact finite difference scheme for two dimensional Helmholtz equation is further improved and a more accurate scheme is presented for the two dimensional Helmholtz equation which is also compact. The novel feature of the present scheme is that it is less sensitive to the associated wave number when compared with that for available sixth order schemes. Theoretical analysis is presented for the newly constructed scheme. The high accuracy of the proposed scheme is illustrated by comparing numerical solutions for solving the two dimensional Helmholtz equations using available sixth-order schemes and the present scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Al-Said, E.A., Noor, M.A., Al-Shejari, A.A.: Numerical solutions for system of second order boundary value problems. Korean J. Comput. Appl. Math. 5(3), 659–667 (1998)

    MathSciNet  MATH  Google Scholar 

  2. Ames, W.F.: Numerical Methods for Partial Differential Equations. Academic press, Cambridge (2014)

    Google Scholar 

  3. Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM J. Numer. Anal. 34(6), 2392–2423 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bayliss, A., Goldstein, C.I., Turkel, E.: The numerical solution of the Helmholtz equation for wave propagation problems in underwater acoustics. Comput. Math. Appl. 11(7–8), 655–665 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chawla, M.M.: A sixth-order tridiagonal finite difference method for general non-linear two-point boundary value problems. IMA J. Appl. Math. 24(1), 35–42 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  7. Dastour, H., Liao, W.: A fourth-order optimal finite difference scheme for the Helmholtz equation with PML. Comput. Math. Appl. 78(6), 2147–2165 (2019)

    Article  MathSciNet  Google Scholar 

  8. Feng, X., Wu, H.: Discontinuous Galerkin methods for the Helmholtz equation with large wave number. SIAM J. Numer. Anal. 47(4), 2872–2896 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Fournié, M., Karaa, S.: Iterative methods and high-order difference schemes for 2D elliptic problems with mixed derivative. J. Appl. Math. Comput. 22(3), 349–363 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fu, Y.: Compact fourth-order finite difference schemes for Helmholtz equation with high wave numbers. J. Comput. Math. 26, 98–111 (2008)

    MathSciNet  MATH  Google Scholar 

  11. Hackbusch, W.: Iterative solution of large sparse systems of equations. Springer, Berlin (1994)

    Book  MATH  Google Scholar 

  12. Harari, I., Hughes, T.J.R.: Finite element methods for the Helmholtz equation in an exterior domain: model problems. Comput. Methods Appl. Mech. Eng. 87(1), 59–96 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  13. Harari, I., Turkel, E.: Accurate finite difference methods for time-harmonic wave propagation. J. Comput. Phys. 119(2), 252–270 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  14. Ihlenburg, F., Babuška, I.M.: Finite element solution of the Helmholtz equation with high wave number Part I: The h-version of the FEM. Comput. Math. Appl. 30(9), 9–37 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  15. Ihlenburg, F., Babuška, I.M.: Finite element solution of the Helmholtz equation with high wave number part II: the hp version of the FEM. SIAM J. Numer. Anal. 34(1), 315–358 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  16. Manohar, R.P., Stephenson, J.W.: Single cell high order difference methods for the Helmholtz equation. J. Comput. Phys. 51(3), 444–453 (1983)

    Article  MATH  Google Scholar 

  17. Nabavi, M., Siddiqui, M.H.K., Dargahi, J.: A new 9-point sixth-order accurate compact finite-difference method for the Helmholtz equation. J. Sound Vib. 307(3), 972–982 (2007)

    Article  Google Scholar 

  18. Patel, K.S., Mehra, M.: A numerical study of Asian option with high-order compact finite difference scheme. J. Appl. Math. Comput. 57(1–2), 467–491 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  19. Peiró, J., Sherwin, S.: Finite difference, finite element and finite volume methods for partial differential equations. In: Yip, S. (ed.) Handbook of materials modeling, 2415–2446. Springer (2005)

  20. Settle, S.O., Douglas, C.C., Kim, I., Sheen, D.: On the derivation of highest-order compact finite difference schemes for the one-and two-dimensional Poisson equation with Dirichlet boundary conditions. SIAM J. Numer. Anal. 51(4), 2470–2490 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Shaw, R.P.: Integral equation methods in acoustics. Bound. Elem. X 4, 221–244 (1988)

    MathSciNet  Google Scholar 

  22. Sheu, T.W.H., Hsieh, L.W., Chen, C.F.: Development of a three-point sixth-order Helmholtz scheme. J. Comput. Acoust. 16(3), 343–359 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  23. Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  24. Singer, I., Turkel, E.: Sixth-order accurate finite difference schemes for the Helmholtz equation. J. Comput. Acoust. 14(3), 339–351 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  25. Sutmann, G.: Compact finite difference schemes of sixth order for the Helmholtz equation. J. Comput. Appl. Math. 203(1), 15–31 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  26. Thomas, J.W.: Numerical Partial Differential Equations: Conservation Laws and Elliptic Equations. Springer, Berlin (2013)

    Google Scholar 

  27. Turkel, E., Gordon, D., Gordon, R., Tsynkov, S.: Compact 2D and 3D sixth order schemes for the Helmholtz equation with variable wave number. J. Comput. Phys. 232(1), 272–287 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wu, T., Xu, R.: An optimal compact sixth-order finite difference scheme for the Helmholtz equation. Comput. Math. Appl. 75, 2520–2537 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  29. Young, D.M.: Iterative Solution of Large Linear Systems. Elsevier, Amsterdam (2014)

    Google Scholar 

  30. Zhang, Y., Wang, K., Guo, R.: Sixth-order finite difference scheme for the Helmholtz equation with inhomogeneous Robin boundary condition. Adv. Differ. Equ. 2019(1), 362 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors sincerely thank the editor and anonymous referees for detailed and very helpful suggestions and comments which significantly improved the presentation of this paper. The research work to the first author is supported by SRM Institute of Science and Technology Kattankulathur, Tamil Nadu India. The authors also acknowledge the SERB, New Delhi, India towards computational facility through project file No. MTR/2017/000187. Discussions with Dr. Shuvam Sen is also acknowledged.

Author information

Authors and Affiliations

  1. Research Institute, SRM Institute of Science & Technology, Kattankulathur, Kancheepuram, Tamil Nadu, 603 203, India

    Neelesh Kumar

  2. Research Institute & Department of Mathematics, SRM Institute of Science & Technology, Kattankulathur, Tamil Nadu, 603 203, India

    Ritesh Kumar Dubey

Authors
  1. Neelesh Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ritesh Kumar Dubey
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Neelesh Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the SRMIST, Tamil Nadu; and SERB New Delhi, India under Grant [MTR/2017/000187].

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, N., Dubey, R.K. A new development of sixth order accurate compact scheme for the Helmholtz equation. J. Appl. Math. Comput. 62, 637–662 (2020). https://doi.org/10.1007/s12190-019-01301-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-019-01301-x

Keywords

Mathematics Subject Classification