Abstract
The non-waiting constraint is a crucial factor in industries with continuous production flows. Recognizing the significance of this constraint in the manufacturing process, we propose several approaches to minimize the maximum tardiness in the no-wait manufacturing flow shop scheduling problem. This research presents two main approaches: an exact method that utilizes mixed integer linear programming and an approximate method based on constructive heuristics and hybrid meta-heuristics. To tackle the problem, we introduce multiple heuristics and hybrid improved meta-heuristics based Nawaz Enscore Ham, greedy randomized adaptive search procedure and genetic algorithm. Furthermore, we propose three hybrid meta-heuristics based on the simulated annealing approach. To validate the effectiveness and robustness of our methods, we conducted experiments on multiple instances of the flow shop problem proposed by Taillard. The results demonstrate that the hybrid algorithm, which combines a greedy randomized adaptive search procedure with the insertion procedure and simulated annealing, exhibits strong performance. In fact, this algorithm achieved a success rate of \(72\%\) across 200 test instances. It outperformed the other two meta-heuristics, with a minimum average relative percentage deviation of only \(0.0039\%\).
















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Availability of data and materials
No datasets were generated or analysed during the current study.
References
Tighazoui A, Sauvey C, Sauer N (2023) Heuristics for flow shop rescheduling with mixed blocking constraints. TOP 32:1–33
Alawad NA, Abed-alguni BH (2022) Discrete Jaya with refraction learning and three mutation methods for the permutation flow shop scheduling problem. J Supercomput 78:1–22
Kacem A, Dammak A (2021) Multi-objective scheduling on two dedicated processors. TOP 29(3):694–721
Jiang Y, Yin S (2017) Recent results on key performance indicator oriented fault detection using the DB-KIT toolbox. In: IECON 2017-43rd annual conference of the IEEE industrial electronics society. IEEE, pp 7103–7108
Nawaz M, Enscore EE Jr, Ham I (1983) A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 11(1):91–95
Prabhaharan G, Khan BSH, Rakesh L (2006) Implementation of grasp in flow shop scheduling. Int J Adv Manuf Technol 30:1126–1131
Rajendran C (1994) A no-wait flowshop scheduling heuristic to minimize makespan. J Oper Res Soc 45(4):472–478
Hall NG, Sriskandarajah C (1996) A survey of machine scheduling problems with blocking and no-wait in process. Oper Res 44(3):510–525
Zhao F, Zhang L, Liu H, Zhang Y, Ma W, Zhang C et al (2019) An improved water wave optimization algorithm with the single wave mechanism for the no-wait flow-shop scheduling problem. Eng Optim 51(10):1727–1742
Pan QK, Tasgetiren MF, Liang YC (2008) A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem. Comput Oper Res 35(9):2807–2839
Cascone A, D’Apice C, Piccoli B, Rarità L (2008) Circulation of car traffic in congested urban areas. Commun Math Sci 6(3):765–784
D’Apice C, Manzo R, Piccoli B (2012) Optimal input flows for a PDE-ODE model of supply chains. Commun Math Sci 10(4):1225–1240
D’Arienzo MP, Rarità L (2020) Management of supply chains for the wine production. In: AIP conference proceedings, vol 2293. AIP Publishing
Rarità L et al (2020) Optimization approaches to manage congestions for the phenomenon “Luci D’Artista” in Salerno. In: Proceedings of 32nd European modeling and simulation symposium, EMSS 2020, pp 319–324
D’Arienzo MP, Rarità L (2020) Growth effects on the network dynamics with applications to the cardiovascular system. In: AIP conference proceedings, vol 2293. AIP Publishing
de Almeida FS, Nagano MS (2023) An efficient iterated greedy algorithm for a multi-objective no-wait flow shop problem with sequence dependent setup times. 4OR, pp 1–15
Bertolissi E (2000) Heuristic algorithm for scheduling in the no-wait flow-shop. J Mater Process Technol 107(1–3):459–465
Sapkal SU, Laha D (2013) A heuristic for no-wait flow shop scheduling. Int J Adv Manuf Technol 68:1327–1338
Laha D, Sapkal SU (2014) An improved heuristic to minimize total flow time for scheduling in the m-machine no-wait flow shop. Comput Ind Eng 67:36–43
Kz Gao, Qk Pan, Jq Li (2011) Discrete harmony search algorithm for the no-wait flow shop scheduling problem with total flow time criterion. Int J Adv Manuf Technol 56:683–692
Akhshabi M, Tavakkoli-Moghaddam R, Rahnamay-Roodposhti F (2014) A hybrid particle swarm optimization algorithm for a no-wait flow shop scheduling problem with the total flow time. Int J Adv Manuf Technol 70:1181–1188
Qi X, Wang H, Zhu H, Zhang J, Chen F, Yang J (2016) Fast local neighborhood search algorithm for the no-wait flow shop scheduling with total flow time minimization. Int J Prod Res 54(16):4957–4972
Zhang S, Gu X, Zhou F (2020) An improved discrete migrating birds optimization algorithm for the no-wait flow shop scheduling problem. IEEE Access 8:99380–99392
Sharma M, Sharma M, Sharma S (2020) Advanced metaheuristics for bicriteria no-wait flow shop scheduling problem. In: Soft computing for problem solving 2019: proceedings of SocProS 2019, vol 1. Springer, Berlin, pp 121–135
Bewoor LA, Chandra Prakash V, Sapkal SU (2017) Evolutionary hybrid particle swarm optimization algorithm for solving NP-hard no-wait flow shop scheduling problems. Algorithms 10(4):121
AitZai A, Benmedjdoub B, Boudhar M (2016) Branch-and-bound and PSO algorithms for no-wait job shop scheduling. J Intell Manuf 27:679–688
Zhao F, Qin S, Yang G, Ma W, Zhang C, Song H (2019) A factorial based particle swarm optimization with a population adaptation mechanism for the no-wait flow shop scheduling problem with the makespan objective. Expert Syst Appl 126:41–53
Samarghandi H (2019) Solving the no-wait job shop scheduling problem with due date constraints: a problem transformation approach. Comput Ind Eng 136:635–662
Valenzuela-Alcaraz VM, Cosio-Leon M, Romero-Ocaño AD, Brizuela CA (2022) A cooperative coevolutionary algorithm approach to the no-wait job shop scheduling problem. Expert Syst Appl 194:116498
Riahi V, Kazemi M (2018) A new hybrid ant colony algorithm for scheduling of no-wait flowshop. Oper Res Int J 18:55–74
Pan QK, Wang L, Zhao BH (2008) An improved iterated greedy algorithm for the no-wait flow shop scheduling problem with makespan criterion. Int J Adv Manuf Technol 38:778–786
Qian B, Wang L, Hu R, Huang D, Wang X (2009) A DE-based approach to no-wait flow-shop scheduling. Comput Ind Eng 57(3):787–805
Zhao F, He X, Wang L (2020) A two-stage cooperative evolutionary algorithm with problem-specific knowledge for energy-efficient scheduling of no-wait flow-shop problem. IEEE Trans Cybern 51(11):5291–5303
Yüksel D, Taşgetiren MF, Kandiller L, Gao L (2020) An energy-efficient bi-objective no-wait permutation flowshop scheduling problem to minimize total tardiness and total energy consumption. Comput Ind Eng 145:106431
Wu X, Che A (2020) Energy-efficient no-wait permutation flow shop scheduling by adaptive multi-objective variable neighborhood search. Omega 94:102117
Zhao F, Liu H, Zhang Y, Ma W, Zhang C (2018) A discrete water wave optimization algorithm for no-wait flow shop scheduling problem. Expert Syst Appl 91:347–363
Zhao F, Zhang L, Liu H, Zhang Y, Ma W, Zhang C et al (2018) An improved water wave optimization algorithm with the single wave mechanism for the no-wait flow-shop scheduling problem. Eng Optim 51:1727–1742
Engin O, Güçlü A (2018) A new hybrid ant colony optimization algorithm for solving the no-wait flow shop scheduling problems. Appl Soft Comput 72:166–176
Sun H, Jiang A, Ge D, Zheng X, Gao F (2021) A chance constrained programming approach for no-wait flow shop scheduling problem under the interval-valued fuzzy processing time. Processes 9(5):789
Bougloula AE (2023) Optimizing the job shop scheduling problem with a no wait constraint by using the Jaya algorithm approach. Manag Prod Eng Rev 14(3):148–155
Mahdavi K, Mohammadi M, Ahmadizar F (2023) Efficient scheduling of a no-wait flexible job shop with periodic maintenance activities and processing constraints. J Qual Eng Prod Optim
Lin YK, Yen CH (2023) Genetic algorithm for solving the no-wait three-stage surgery scheduling problem. Healthcare 11:739
Rahimi A, Hejazi SM, Zandieh M, Mirmozaffari M (2023) A novel hybrid simulated annealing for no-wait open-shop surgical case scheduling problems. Appl Syst Innov 6(1):15
Karacan I, Senvar O, Bulkan S (2023) A novel parallel simulated annealing methodology to solve the no-wait flow shop scheduling problem with earliness and tardiness objectives. Processes 11(2):454
Yu J, Zhang H, Dong Y (2023) Research on no-wait flow shop scheduling based on discrete state transition algorithm. J Syst Simul 35(5):1034–1045
Koulamas C, Kyparisis GJ (2021) The no-wait flow shop with rejection. Int J Prod Res 59(6):1852–1859
Zhao F, He X, Zhang Y, Lei W, Ma W, Zhang C et al (2020) A jigsaw puzzle inspired algorithm for solving large-scale no-wait flow shop scheduling problems. Appl Intell 50:87–100
Miyata HH, Nagano MS, Gupta JN (2019) Incorporating preventive maintenance into the m-machine no-wait flow-shop scheduling problem with total flow-time minimization: a computational study. Eng Optim 51(4):680–698
Aqil S (2024) Effective population-based meta-heuristics with NEH and GRASP heuristics minimizing total weighted flow time in no-wait flow shop scheduling problem under sequence-dependent setup time constraint. Arab J Sci Eng 1:1–24
Shao W, Pi D, Shao Z (2017) An extended teaching-learning based optimization algorithm for solving no-wait flow shop scheduling problem. Appl Soft Comput 61:193–210
Pereira MT, Nagano MS (2022) Hybrid metaheuristics for the integrated and detailed scheduling of production and delivery operations in no-wait flow shop systems. Comput Ind Eng 170:108255
Li J, Guo X, Zhang Q (2023) Multi-strategy discrete teaching-learning-based optimization algorithm to solve no-wait flow-shop-scheduling problem. Symmetry 15(7):1430
Smutnicki C, Pempera J, Bocewicz G, Banaszak Z (2022) Cyclic flow-shop scheduling with no-wait constraints and missing operations. Eur J Oper Res 302(1):39–49
Allahverdi A, Aydilek H, Aydilek A (2022) An algorithm for a no-wait flowshop scheduling problem for minimizing total tardiness with a constraint on total completion time. Int J Ind Eng Comput 13(1):43–50
Başar R, Engin O (2022) A no-wait flow shop scheduling problem with setup time in fuzzy environment. In: Intelligent and fuzzy techniques for emerging conditions and digital transformation: proceedings of the INFUS 2021 conference, held August 24–26, 2021, vol 1, Springer, Berlin, pp 607–614
Deng G, Wei M, Zhang S, Xu M, Jiang T, Wang F (2024) A simple migrating birds optimization algorithm with two search modes to solve the no-wait job shop problem. Expert Syst Appl 238:122112
Mirmozaffari M, Hejazi SM, Karamizadeh N, Montazeri A (2024) A mixed-integer non-linear no-wait open-shop scheduling model for minimizing makespan and total tardiness in manufacturing. Decis Anal J 10:100403
Khurshid B, Maqsood S, Khurshid Y, Naeem K, Khalid QS (2024) A hybridization of evolution strategies with iterated greedy algorithm for no-wait flow shop scheduling problems. Sci Rep 14(1):2376
Almeida FSd, Nagano MS (2023) Heuristics to optimize total completion time subject to makespan in no-wait flow shops with sequence-dependent setup times. J Oper Res Soc 74(1):362–373
Prata BdA, Nagano MS (2023) A novel iterated greedy algorithm for no-wait permutation flowshop scheduling to minimize weighted quadratic tardiness. Eng Optim 55(12):2070–2083
Ji N, Gu X (2024) Integration of planning, scheduling, and control of no-wait batch plant. Comput Chem Eng 180:108467
Samarghandi H, Behroozi M (2017) On the exact solution of the no-wait flow shop problem with due date constraints. Comput Oper Res 81:141–159
Alekseeva E, Mezmaz M, Tuyttens D, Melab N (2017) Parallel multi-core hyper-heuristic GRASP to solve permutation flow-shop problem. Concurr Comput: Pract Exp 29(9):e3835
Molina-Sánchez L, González-Neira E (2016) GRASP to minimize total weighted tardiness in a permutation flow shop environment. Int J Ind Eng Comput 7(1):161–176
Bamoumen M, Elfirdoussi S, Ren L, Tchernev N (2023) An efficient GRASP-like algorithm for the multi-product straight pipeline scheduling problem. Comput Oper Res 150:106082
Yepes-Borrero JC, Perea F, Villa F, Vallada E (2023) Flowshop with additional resources during setups: mathematical models and a GRASP algorithm. Comput Oper Res 154:106192
Feo TA, Resende MG (1995) Greedy randomized adaptive search procedures. J Global Optim 6:109–133
Bertsimas D, Tsitsiklis J (1993) Simulated annealing. Stat Sci 8(1):10–15
Amine K (2019) Multiobjective simulated annealing: principles and algorithm variants. Adv Oper Res 2019:8134674
Wei H, Li S, Jiang H, Hu J, Hu J (2018) Hybrid genetic simulated annealing algorithm for improved flow shop scheduling with makespan criterion. Appl Sci 8(12):2621
Osman IH, Potts C (1989) Simulated annealing for permutation flow-shop scheduling. Omega 17(6):551–557
Holland JH (1992) Genetic algorithms. Sci Am 267(1):66–73
Funding
The authors declare that no funding was received for conducting this study.
Author information
Authors and Affiliations
Contributions
Omar Nejjarou: Conceptualization, Methodology, Software, Validation. Said Aqil: Conceptualization, Methodology, Writing—review and editing. Mohamed Lahby: Writing—review and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Numerical illustration
Appendix: Numerical illustration
Our contribution focuses on improving the GRASP algorithm by integrating the Total Permutation Procedure (TPP) and the NEH heuristic. To our knowledge, this is the first time such an improvement has been applied to GRASP algorithms. First, we’ll present the results obtained with TPP. Then, we’ll apply the NEH approach to these same GRASP algorithm results, in order to further evaluate the effectiveness of our proposed enhancement. We’ll compare these results to those found by MILP. For this, we have chose to apply this approach in a production workshop with six jobs \(\{ J_1, J_2, J_3, J_4, J_5, J_6 \}\) to produce three machines \(\{ M_1, M_2, M_3 \}\) in serial workshop. the following matrices show job processing times on the machines, as well as lead times, we will classify these jobs in descending order of the sum of the operating times of each job (\(TP_j= \sum _{i=1}^{m} p_{ij}\)), this allowed us to have the initial sequence \(S_0=\{ J_6, J_3, J_1, J_5, J_4, J_2 \}\). From this initial solution we will start our approach we apply the GRASP algorithm to each iteration and improve the partial solution by the total permutation method.
On this first iteration we have the first job is \(J_6\) we will combine it with the other jobs \(\{J_3, J_1, J_5, J_4, J_2 \}\) and calculated the value of the objective function and deduce the best partial sequence:
IGRN solution
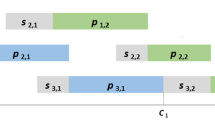
During this phase we have as solution for the first iteration \(S^{gr}_{1} = \{ J_6,J_5 \}\), and we start to insert the other jobs and update the solution; the following figure shows well the first three iterations as well as the results obtained. The Fig. 17 show the last step insertion process using the NEH algorithm in the improved GRASP procedure.
The Fig. 18 illustrate the graphical solution given in IGRN, where the best constructive solution in improved GRASP by NEH is \(S=\{J_4,J_1,J_5,J_3,J_2,J_6\}\). The minimum value of the objective function, denoted as \(T_{max}=38\), is achieved by inserting job \(J_1\) into the previously best sub-sequence.
IGRP solution
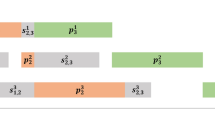
The Fig. 19 depict last iterations of the improved GRASP with TPP, initiated with the \({J_6, J_5}\) job combination. In each iteration, the generated solution is obtained by considering the total permutations within the selected sub-sequence from the RCL set.
In this approach, we utilized the IGRP algorithm to generate a set of solutions by exhaustively permuting the right sub-sequence. This algorithm facilitates extensive exploration of the solution’s neighborhood by examining various job positions. The final step yielded the best solution, denoted as \(S=\{J_6,J_1,J_5,J_4,J_3,J_2\}\). The graphical Gantt chart in Fig. 20 illustrates the resulting scheduling plan, with a maximum tardiness of \(T{max}=43\) attributed to job \(J_2\).
MILP solution
Using the LINGO solver, we found the optimal solution with a value of \(T_{\text {max}} = 34\). This solution is obtained by the sequence \({J_2, J_4, J_3, J_5, J_1, J_6}\), as shown in the Gantt diagram in Fig. 21.
In Figs. 22 and 23 presents the initial solution for instances 20 jobs ans 5 machines of Taillard’s dataset, attained by the two NEH and IGRN, providing visual evidence of the efficacy of these approaches.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Nejjarou, O., Aqil, S. & Lahby, M. Hybrid meta-heuristic solving no-wait flow shop scheduling minimizing maximum tardiness. Evol. Intel. 17, 3935–3959 (2024). https://doi.org/10.1007/s12065-024-00965-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12065-024-00965-0