A novel two-phase hybrid selection mechanism feeder to improve performance of many-objective optimization algorithms | Evolutionary Intelligence Skip to main content
Springer Nature Link
Log in

A novel two-phase hybrid selection mechanism feeder to improve performance of many-objective optimization algorithms

  • Research Paper
  • Published:
Evolutionary Intelligence Aims and scope Submit manuscript

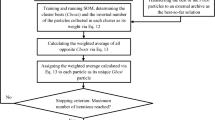
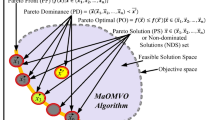
Abstract

Solving many-objective optimization problems has become one of the most popular research areas in recent years due to its ever-increasing applications in industries and other fields. In this paper, a novel two-phase hybrid feeder (TPHF) is proposed to provide elite solutions for selection mechanism of many-objective optimization algorithms (MaOAs) to improve their performance. The proposed TPHF framework generates solutions using a novel particle swarm optimization (PSO) operator along with a genetic algorithm operator during a two-phase calculated search based on the average velocity of the PSO particles. TPHF focuses on the worst solutions of the population to find a better place for them. Therefore, it frequently resets the PSO particles to the worst solutions. The new PSO operator uses the novel idea of dynamic inertia and learning factors and a novel velocity update equation. The classic global bests set of the classic PSO operator is replaced by a PSO feeder which uses the novel idea of using groups of the best/worst solutions to feed the new PSO operator based on the phase of the search. The proposed TPHF is applied to some of the most famous and state-of-the-art MaOAs with their corresponding default parameters. The result of the comparison between these MaOAs with their corresponding TPHF versions on MaF test suite shows a significant improvement in the performance of the TPHF versions in 62.2% of the cases.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: Nsga-ii. IEEE Trans Evolut Comput 6(2):182–197

    Google Scholar 

  2. Soto C et al (2020) Solving the multi-objective flexible job shop scheduling problem with a novel parallel branch and bound algorithm. Swarm Evolut Comput 53:100632

    Google Scholar 

  3. Li Q, Cao Z, Ding W, Li Q (2020) A multi-objective adaptive evolutionary algorithm to extract communities in networks. Swarm Evolut Comput 52:100629

    Google Scholar 

  4. Zhang Y, Gong D-W, Gao X-Z, Tian T, Sun X-Y (2020) Binary differential evolution with self-learning for multi-objective feature selection. Inf Sci 507:67–85

    MathSciNet  Google Scholar 

  5. Abualigah LMQ et al (2019) Feature selection and enhanced krill herd algorithm for text document clustering. Springer, Berlin

    Google Scholar 

  6. Abualigah LM, Khader AT (2017) Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering. J Supercomput 73(11):4773–4795

    Google Scholar 

  7. Yang Y, Yang B, Wang S, Jin T, Li S (2020) An enhanced multi-objective grey wolf optimizer for service composition in cloud manufacturing. Appl Soft Comput 87:106003

    Google Scholar 

  8. Zitzler E (1999) Evolutionary algorithms for multiobjective optimization: Methods and applications, vol 63. Citeseer

  9. Zitzler E, Laumanns M, Thiele L (2019) Spea2: Improving the strength pareto evolutionary algorithm. TIK-report 103

  10. Srinivas N, Deb K (1994) Multiobjective optimization using nondominated sorting in genetic algorithms. Evolut Comput 2(3):221–248

    Google Scholar 

  11. Knowles J, Corne D (1999) The pareto archived evolution strategy: A new baseline algorithm for pareto multiobjective optimisation. IEEE, vol 1. pp 98–105

  12. Zhang X, Zheng X, Cheng R, Qiu J, Jin Y (2018) A competitive mechanism based multi-objective particle swarm optimizer with fast convergence. Inf Sci 427:63–76

    MathSciNet  Google Scholar 

  13. Lin Q, Li J, Du Z, Chen J, Ming Z (2015) A novel multi-objective particle swarm optimization with multiple search strategies. Eur J Op Res 247(3):732–744

    MathSciNet  Google Scholar 

  14. Khare V, Yao X, Deb K (2003) Performance scaling of multi-objective evolutionary algorithms. Springer, pp 376–390

  15. Purshouse RC, Fleming PJ (2003) Evolutionary many-objective optimisation: An exploratory analysis. IEEE, vol 3. pp 2066–2073

  16. Purshouse RC, Fleming PJ (2007) On the evolutionary optimization of many conflicting objectives. IEEE Trans Evolut Comput 11(6):770–784

    Google Scholar 

  17. Chand S, Wagner M (2015) Evolutionary many-objective optimization: a quick-start guide. Surv Op Res Manag Sci 20(2):35–42

    MathSciNet  Google Scholar 

  18. Panichella A (2019) An adaptive evolutionary algorithm based on non-euclidean geometry for many-objective optimization. 595–603

  19. Sun Y, Yen GG, Yi Z (2018) Igd indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans Evolut Comput 23(2):173–187

    Google Scholar 

  20. Coello C, Lamont G, Van Veldhuizen D (2007) Evolutionary algorithms for solving multi-objective problems, 2nd edn. Springer-Verlag, New York Inc

    Google Scholar 

  21. Van Veldhuizen DA (1999) Multiobjective evolutionary algorithms: classifications, analyses, and new innovations. Tech. Rep., Air force Inst of Tech Wright-Patterson AFB OH school of engineering and management

  22. Coello CAC, Lamont GB (2004) Applications of multi-objective evolutionary algorithms, vol 1. World Scientific, Singapore

    Google Scholar 

  23. Coello CAC (2002) Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art. Comput Methods Appl Mech Eng 191(11–12):1245–1287

    ADS  MathSciNet  Google Scholar 

  24. Yuan Y, Xu H, Wang B, Yao X (2015) A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans Evolut Comput 20(1):16–37

    Google Scholar 

  25. Wang H, He S, Yao X (2017) Nadir point estimation for many-objective optimization problems based on emphasized critical regions. Soft Comput 21(9):2283–2295

    Google Scholar 

  26. Das I, Dennis JE (1998) Normal-boundary intersection: A new method for generating the pareto surface in nonlinear multicriteria optimization problems. SIAM J Optim 8(3):631–657

    MathSciNet  Google Scholar 

  27. Zhang X, Tian Y, Jin Y (2014) A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans Evolut Comput 19(6):761–776

    Google Scholar 

  28. Deb K, Miettinen K (2009) A review of nadir point estimation procedures using evolutionary approaches: A tale of dimensionality reduction. 1–14

  29. Deb K, Miettinen K, Chaudhuri S (2010) Toward an estimation of nadir objective vector using a hybrid of evolutionary and local search approaches. IEEE Trans Evolut Comput 14(6):821–841

    Google Scholar 

  30. Michalewicz Z, Fogel DB (2013) How to solve it: modern heuristics. Springer Science & Business Media, Germany

    Google Scholar 

  31. Goldberg DE (1989) Genetic algorithms in search. Optimization, and MachineLearning. Addion wesley

  32. Husbands P (1992) Genetic algorithms in optimisation and adaptation. Halsted Press, Canberra, pp 227–276

    Google Scholar 

  33. Vicini A, Quagliarella D, Vicini A, Quagliarella D (1997) Multipoint transonic airfoil design by means of a multiobjective genetic algorithm. In: 35th Aerospace Sciences Meeting and Exhibit, p 82. https://doi.org/10.2514/6.1997-82

  34. Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. science 220(4598):671–680

    ADS  MathSciNet  CAS  PubMed  Google Scholar 

  35. Osycska A (1984) Multi-Criterion Optimization in Engineering with Fortran Examples. Halstad Press, New York, NY. https://www.worldcat.org/title/multicriterion-optimization-in-engineering-withfortran-programs/oclc/10275539

  36. Glover F, Laguna M (1998) Tabu search. Springer, Boston, pp 2093–2229

    Google Scholar 

  37. Michalewicz Z, Hartley SJ (1996) Genetic algorithms+ data structures= evolution programs. Mathl Intell 18(3):71

    Google Scholar 

  38. Back T (1996) Evolutionary algorithms in theory and practice: Evolution strategies, evolutionary programming, genetic algorithms. Oxford University Press, United Kingdom

    Google Scholar 

  39. Eberhart R, Kennedy J (1995) Particle swarm optimization. Citeseer, vol 4. pp 1942–1948

  40. Mirjalili S, Mirjalili SM, Hatamlou A (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 27(2):495–513

    Google Scholar 

  41. Abualigah L (2020) Multi-verse optimizer algorithm: a comprehensive survey of its results, variants, and applications. Neural Comput Appl 32(16):12381–12401

    Google Scholar 

  42. Lamont GB (1993) Compendium of Parallel Programs for the Intel iPSC Computers. Wright-Patterson AFB, OH 45433

  43. Fogel DB, Computation E (1995) Toward a new philosophy of machine intelligence. IEEE Evolut Comput

  44. Deb K (2001) Multi-objective optimization using evolutionary algorithms, vol 16. John Wiley, New Jersey

    Google Scholar 

  45. Garza-Fabre M, Pulido GT, Coello CAC (2009) Ranking methods for many-objective optimization. Springer, pp 633–645

  46. Deb K, Jain H (2013) An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: solving problems with box constraints. IEEE Trans Evolut Comput 18(4):577–601

    Google Scholar 

  47. Zhu Q et al (2019) An elite gene guided reproduction operator for many-objective optimization. IEEE Trans Cybern 51(2):765–778

    Google Scholar 

  48. Jiang S, He X, Zhou Y (2019) Many-objective evolutionary algorithm based on adaptive weighted decomposition. Appl Soft Comput 84:105731

    Google Scholar 

  49. Chen G, Li J (2019) A diversity ranking based evolutionary algorithm for multi-objective and many-objective optimization. Swarm Evolut Comput 48:274–287

    Google Scholar 

  50. Zhang Q, Li H (2007) Moea/d: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evolut Comput 11(6):712–731

    Google Scholar 

  51. Liang Z, Zeng J, Liu L, Zhu Z (2021) A many-objective optimization algorithm with mutation strategy based on variable classification and elite individual. Swarm Evolut Comput 60:100769

    Google Scholar 

  52. Zou X, Chen Y, Liu M, Kang L (2008) A new evolutionary algorithm for solving many-objective optimization problems. IEEE Trans Syst Man Cybern Part B (Cybernetics) 38(5):1402–1412

    Google Scholar 

  53. Bader J, Zitzler E (2011) Hype: an algorithm for fast hypervolume-based many-objective optimization. Evolut Comput 19(1):45–76

    Google Scholar 

  54. Liang Z, Hu K, Ma X, Zhu Z (2019) A many-objective evolutionary algorithm based on a two-round selection strategy. IEEE Trans Cybern 51(3):1417–1429

    Google Scholar 

  55. Cheng R, Jin Y, Olhofer M, Sendhoff B (2016) A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans Evolut Comput 20(5):773–791

    Google Scholar 

  56. Coello CC, Lechuga MS (2002) Mopso: A proposal for multiple objective particle swarm optimization. IEEE, vol 2. pp 1051–1056

  57. Dai C, Wang Y, Ye M (2015) A new multi-objective particle swarm optimization algorithm based on decomposition. Inf Sci 325:541–557

    Google Scholar 

  58. Zapotecas Martínez S, Coello Coello CA (2011) A multi-objective particle swarm optimizer based on decomposition. pp. 69–76

  59. Nebro AJ et al (2009) Smpso: A new pso-based metaheuristic for multi-objective optimization. IEEE, pp 66–73

  60. Peng W, Zhang Q (2008) A decomposition-based multi-objective particle swarm optimization algorithm for continuous optimization problems. IEEE, pp 534–537

  61. Sierra MR, Coello Coello CA (2005) Improving pso-based multi-objective optimization using crowding, mutation and \(\epsilon\)-dominance. Springer, pp 505–519

  62. Zhan Z-H et al (2013) Multiple populations for multiple objectives: a co-evolutionary technique for solving multi-objective optimization problems. IEEE Trans Cybern 43(2):445–463

    PubMed  Google Scholar 

  63. Knowles JD, Corne DW (2000) Approximating the nondominated front using the pareto archived evolution strategy. Evolut Comput 8(2):149–172

    CAS  Google Scholar 

  64. Hu W, Yen GG (2013) Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system. IEEE Trans Evolut Comput 19(1):1–18

    CAS  Google Scholar 

  65. Zitzler E, Thiele L (1998) Multiobjective optimization using evolutionary algorithms–a comparative case study. Springer, pp 292–301

  66. Ding R, Dong H, He J, Li T (2019) A novel two-archive strategy for evolutionary many-objective optimization algorithm based on reference points. Appl Soft Comput 78:447–464

    Google Scholar 

  67. Luo J, Huang X, Li X, Gao K (2019) A novel particle swarm optimizer for many-objective optimization. IEEE, pp 958–965

  68. Lin Q et al (2016) Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems. IEEE Trans Evolut Comput 22(1):32–46

    Google Scholar 

  69. Tian Y, Cheng R, Zhang X, Jin Y (2017) Platemo: A matlab platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput Intell Mag 12(4):73–87

    Google Scholar 

  70. Sindhya K, Miettinen K, Deb K (2012) A hybrid framework for evolutionary multi-objective optimization. IEEE Trans Evolut Comput 17(4):495–511

    Google Scholar 

  71. Lin Q et al (2015) A hybrid evolutionary immune algorithm for multiobjective optimization problems. IEEE Trans Evolut Comput 20(5):711–729

    Google Scholar 

  72. Tian Y, Zheng X, Zhang X, Jin Y (2019) Efficient large-scale multiobjective optimization based on a competitive swarm optimizer. IEEE Trans Cybern 50(8):3696–3708

    PubMed  Google Scholar 

  73. Cheng R et al (2017) A benchmark test suite for evolutionary many-objective optimization. Complex Intell Syst 3(1):67–81

    Google Scholar 

  74. Huband S, Hingston P, Barone L, While L (2006) A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans Evolut Comput 10(5):477–506

    Google Scholar 

  75. Deb K, Thiele L, Laumanns M, Zitzler E (2005) Scalable test problems for evolutionary multiobjective optimization. Springer, London, pp 105–145

    Google Scholar 

  76. Jain H, Deb K (2013) An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part ii: handling constraints and extending to an adaptive approach. IEEE Trans Evolut Comput 18(4):602–622

    Google Scholar 

  77. Brockhoff D, Zitzler E (2009) Objective reduction in evolutionary multiobjective optimization: theory and applications. Evolut Comput 17(2):135–166

    Google Scholar 

  78. Deb K, Saxena D, et al (2006) Searching for pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems. pp. 3352–3360

  79. Köppen M, Yoshida K (2007) Substitute distance assignments in nsga-ii for handling many-objective optimization problems. Springer, pp 727–741

  80. Ishibuchi H, Hitotsuyanagi Y, Tsukamoto N, Nojima Y (2010) Many-objective test problems to visually examine the behavior of multiobjective evolution in a decision space. Springer, pp 91–100

  81. Li M, Grosan C, Yang S, Liu X, Yao X (2017) Multiline distance minimization: a visualized many-objective test problem suite. IEEE Trans Evolut Comput 22(1):61–78

    Google Scholar 

  82. Saxena DK, Zhang Q, Duro JA, Tiwari A (2011) Framework for many-objective test problems with both simple and complicated pareto-set shapes. Springer, pp 197–211

  83. Cheng R, Jin Y, Olhofer M et al (2016) Test problems for large-scale multiobjective and many-objective optimization. IEEE Trans Cybern 47(12):4108–4121

    PubMed  Google Scholar 

  84. Zitzler E, Thiele L, Laumanns M, Fonseca CM, Da Fonseca VG (2003) Performance assessment of multiobjective optimizers: an analysis and review. IEEE Trans Evolut Comput 7(2):117–132

    Google Scholar 

  85. Mann HB, Whitney DR (1947 ) On a test of whether one of two random variables is stochastically larger than the other. Annals Mathematical Stat. 18(1):50–60. https://doi.org/10.1214/aoms/1177730491 ,https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-18/issue-1/On-a-Test-of-Whether-one-of-Two-Random-Variables/10.1214/aoms/1177730491.full

  86. Steel RGD, Torrie JH (1986) Principles and procedures of statistics: a biometrical approach. McGraw-Hill, New York

    Google Scholar 

  87. Chaffi BN, Tafreshi FS (2019) Nasseh method to visualize high-dimensional data. Appl Soft Comput 84:105722

    Google Scholar 

Download references

Acknowledgements

We wish to acknowledge the efforts of Mrs. Narges Sayyadi for proofreading this paper.

Author information

Author notes

  1. M. Rahmani contributed equally to this work.

Authors and Affiliations

  1. Computer Engineering, Arak University, Sardasht, Arak, 38156-8-8349, Markazi, Iran

    Babak Nasseh Chaffi & Mohsen Rahmani

Authors
  1. Babak Nasseh Chaffi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohsen Rahmani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Babak Nasseh Chaffi.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nasseh Chaffi, B., Rahmani, M. A novel two-phase hybrid selection mechanism feeder to improve performance of many-objective optimization algorithms. Evol. Intel. 17, 889–920 (2024). https://doi.org/10.1007/s12065-022-00763-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12065-022-00763-6

Keywords

Search

Navigation