Abstract
Evolution is a highly complex multilevel process and mathematical modeling of evolutionary phenomenon requires proper abstraction and radical reduction to essential features. Examples are natural selection, Mendel’s laws of inheritance, optimization by mutation and selection, and neutral evolution. An attempt is made to describe the roots of evolutionary theory in mathematical terms. Evolution can be studied in vitro outside cells with polynucleotide molecules. Replication and mutation are visualized as chemical reactions that can be resolved, analyzed, and modeled at the molecular level, and straightforward extension eventually results in a theory of evolution based upon biochemical kinetics. Error propagation in replication commonly results in an error threshold that provides an upper bound for mutation rates. Appearance and sharpness of the error threshold depend on the fitness landscape, being the distribution of fitness values in genotype or sequence space. In molecular terms, fitness landscapes are the results of two consecutive mappings from sequences into structures and from structures into the (nonnegative) real numbers. Some properties of genotype–phenotype maps are illustrated well by means of sequence–structure relations of RNA molecules. Neutrality in the sense that many RNA sequences form the same (coarse grained) structure is one of these properties, and characteristic for such mappings. Evolution cannot be fully understood without considering fluctuations—each mutant originates form a single copy, after all. The existence of neutral sets of genotypes called neutral networks, in particular, necessitates stochastic modeling, which is introduced here by simulation of molecular evolution in a kind of flowreactor.











Similar content being viewed by others
Notes
There is also a third stationary state defined by ϕ = 0. For strictly positive fitness values, f i > 0 ∀ i = 1, 2, …, n, this condition can only be fulfilled by x i = 0 ∀ i = 1, 2, …, n, which is identical to state (i). If some f i values are zero—corresponding to lethal variants—the respective variables vanish in the infinite time limit because of dx i /dt = −ϕ(t) x i with ϕ(t) > 0.
All chromosomes are autosomes except the sexual chromosomes X and Y.
In case matrix A is not symmetric, the dynamical system (10) may show more complex dynamics like oscillations, deterministic chaos, etc.
Protein synthesis in vivo is regulated by a complex network controlling gene activity called gene expression. The network involves regulation of transcription (DNA → RNA), post-transcriptional modification and maturation of the messenger-RNA, its translation into protein, and post-translational modification before the protein unfolds its function.
Qβ-replicase is an enzyme consisting of four subunits. Three subunits are host proteins involved in translation, the ribosomal protein S1 and the elongation factors Ef-Tu and Ef-Ts. The fourth subunit is a virus-specific protein encoded by the viral RNA.
Standard amplification of single stranded DNA by means of the polymerase chain reaction (PCR) is a frequently used technique for replication that circumvents isothermal duplex dissociation by means of a temperature program: Single stranded DNA is completed to a double helical duplex by means of a polymerase from Thermophilus aquaticus (Taq), the duplex is dissociated into single stands at higher temperature, and cooling of single strands completes the cycle (see also Cahill et al. 1991).
A square non-negative matrix T = {t ij ; i, j = 1, …, n; t ij ≥ 0} is called primitive if there exists a positive integer m such that T m is strictly positive: T m > 0 which implies T m = {t (m) ij ; i, j = 1, …, n; t (m) ij > 0}.
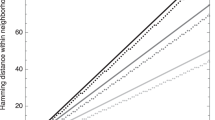
The Hamming distance d H ij between two strings, X i and X j of equal length counts the number of positions in which the two end-to-end aligned strings differ (Hamming 1986).
It can be proven by means of a recursion that the eigenvalues of the matrix \(\tilde{{W}}\) fulfill the relation \(\lambda^{n-1}\left(\lambda-\kappa^{-\ell} \sum\nolimits_{i=1}^nf_i\right)=0.\)
A sharp transition from the structured quasi-species to the uniform distribution is found for the single-peak landscape and some related landscapes only (see “Fitness landscapes and error thresholds” section.
The data obtained from biomolecules suggest a high degree of ruggedness for the landscapes derived for structures and functions: nearby sequences may lead to identical or very different structures. By the same token functions like fitness values may be the same or very different for close by lying genotypes. Ruggedness is an intrinsic property of mapping from biopolymer sequences into structures or functions.
Compatibility means that the sequence can form the structure but not necessarily as the minimum free energy structure.
It is important to stress two facts about relay series: (i) The same shape may appear two or more times in a given relay series series. Then, it was extinct between two consecutive appearances. (ii) A relay series is not a genealogy which is the full recording of parent-offspring relations a time-ordered series of genotypes.
Identical means here that everything was kept unchanged in the computer experiments except the seeds for the random number generator.
Efficiency of evolutionary optimization is measured by average and best fitness values obtained in populations after a predefined number of generations.
References
Biebicher CK, Luce R (1992) In vitro recombination and terminal elongation of RNA by Qβ replicase. EMBO J 11(13):5129–5135
Biebricher C, Eigen M (1988) Kinetics of RNA replication by Qβ replicase. In: Domingo E, Holland J, Ahlquist P (eds) RNA genetics, vol I. CRC Press, Boca Raton, pp. 1–21
Biebricher CK, Eigen M, William C, Gardiner J (1983) Kinetics of RNA replication. Biochemistry 22:2544–2559
Biebricher CK, Eigen M, William C, Gardiner J (1984) Kinetics of RNA replication: plus-minus asymmetry and double-strand formation. Biochemistry 23:3186–3194
Biebricher CK, Eigen M, William C, Gardiner J (1985) Kinetics of RNA replication:competition and selection among self-replicating RNA species. Biochemistry 24:6550–6560
Blount ZD, Z C, Lenski RE (2008) Historical contingency an the evolution of a key innovation in an experimental population of Escherichia coli. Proc Natl Acad Sci USA 105:7898–7906
Blythe RA, McKane A (2007) Stochastic models of evolution in genetice, ecology and linguistics. J Stat Mech P07018:1–58
Brown D, Gold L (1996) RNA replication by Qβ replicase: a working model. Proc Natl Acad Sci USA 93:11558–11562
Cahill P, Foster K, Mahan DE (1991) Polymerase chain reaction and Qβ replicase amplification. Clin Chem 37:1482–1485
Darwin C (1859) On the origin of species by means of natural selection or the preservation of favoured races in the struggle for life. John Murray, London
Demetrius L, Schuster P, Sigmund K (1985) Polynucleotide evolution and branching processes. Bull Math Biol 47:239–262
Derrida B, Peliti L (1991) Evolution in a flat fittness landscape. Bull Math Biol 53:355–382
Dimitrov RA, Zuker M (2004) Prediction of hybridization and melting for double-stranded nucleic acids. Biophys J 87:215–226
Dobzhansky T, Ayala FJ, Stebbins GL, Valentine JW (1977) Evolution. W. H. Freeman & Co., San Francisco
Domingo E (ed) (2005) Virus entry into error catastrophe as a new antiviral strategy. Virus Res 107(2):115–228
Drake JW (1993) Rates of spontaneous mutation among RNA viruses. Proc Natl Acad Sci USA 90:4171–4175
Drake JW, Charlesworth B, Charlesworth D, Crow JF (1998) Rates of spontaneous mutation. Genetics 148:1667–1686
Edwards AW (1994) The fundamental theroem of natural selection. Biol Rev 69:443–474
Eigen M (1971) Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 58:465–523
Eigen M, Biebricher C (1988) Sequence space and quasispecies distribution. In: Domingo E, Holland J, Ahlquist P (eds) RNA Genetics, vol III, CRC Press, Boca Raton, pp 211–245
Eigen M, McCaskill J, Schuster P (1989) The molecular quasispecies. Adv Chem Phys 75:149–263
Fisher RA (1930) The genetical theory of natural selection. Oxford University Press, Oxford
Fontana W, Schuster P (1987) A computer model of evolutionary optimization. Biophys Chem 26:123–147
Fontana W, Schuster P (1998a) Continuity in evolution: on the nature of transitions. Science 280:1451–1455
Fontana W, Schuster P (1998b) Shaping space. The possible and the attainable in RNA genotype-phenotype mapping. J Theor Biol 194:491–515
Fontana W, Schnabl W, Schuster P (1989) Physical aspects of evolutionary optimization and adaptation. Phys Rev A 40:3301–3321
Fontana W, Konings DAM, Stadler PF, Schuster P (1993) Statistics of RNA secondary structures. Biopolymers 33:1389–1404
Gillespie DT (1976) A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comp Phys 22:403–434
Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81:2340–2361
Gillespie DT (2007) Stochastic simulation of chemical kinetics. Annu Rev Phys Chem 58:35–55
Hamming RW (1986) Coding and information theory, 2nd edn. Prentice-Hall, Englewood Cliffs
Held DM, Greathouse ST, Agrawal A, Burke DH (2003) Evolutionary landscapes for the acquisition of new ligand recognition by RNA aptamers. J Mol Evol 57:299–308
Hofacker IL, Fontana W, Stadler PF, Bonhoeffer LS, Tacker M, Schuster P (1994a) Fast folding and comparison of RNA secondary structures. Monatshefte für Chemie 125:167–188
Hofacker IL, Fontana W, Stadler PF, Bonhoeffer LS, Tacker M, Schuster P (1994b) Vienna RNA package. Current Version 1.8.4. Institute for Theoretical Chemistry, University of Vienna, Vienna.
Hosoda K, Matsuura T, Kita H, Ichihashi N, Tsukada K, Yomo T (2007) Kinetic analysis of the entire RNA amplification process by Qβ replicase. J Biol Chem 282:15516–15527
Huang Z, Szostak JW (2003) Evolution of aptamers with a new specificity and new secondary structures from an ATP aptamer. RNA 9:1456–1463
Huynen MA, Stadler PF, Fontana W (1996) Smoothness within ruggedness. The role of neutrality in adaptation. Proc Natl Acad Sci USA 93:397–401
Jones BL, Leung HK (1981) Stochastic analysis of a non-linear model for selection of biological macromolecules. Bull Math Biol 43:665–680
Jones BL, Enns RH, Rangnekar SS (1976) On the theory of selection of coupled macromolecular systems. Bull Math Biol 38:15–28
Joyce GF (2007) Forty years of in vitro evolution. Angew Chem Int Ed 46:6420–6436
Judson H (1979) The eighth day of creation. The makers of the revolution in biology. Jonathan Cape, London
Kimura M (1983) The neutral theory of molecular evolution. Cambridge University Press, Cambridge
Kupczok A, Dittrich P (2006) Determinants of simulated RNA evolution. J Theor Biol 238:726–735
Küppers B, Sumper M (1975) Minimal requirements for template recognition by bacteriophage Qβ replicase: approach to general RNA-dependent RNA synthesis. Proc Natl Acad Sci USA 72:2640–2643
Lenski RE, Rose MR, Simpson SC, Tadler SC (1991) Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2,000 generations. Am Nat 38:1315–1341
Leontis NB, Lescoute A, Westhof E (2006) The building blocks and motifs of RNA architecture. Curr Opin Struct Biol 16:279–287
Lincoln TA, Joyce GF (2009) Self-sustained replication of an RNA enzyme. Science 323:1229–1232
Malthus TR (1798) An Essay of the principle of population as it affects the future improvement of society. J. Johnson, London
Maxam A, Gilbert W (1977) A new method of sequencing DNA. Proc Natl Acad Sci USA 74:560–564
McCaskill JS (1984) A localization threshold for macromolecular quasispecies from continuously distributed replication rates. J Chem Phys 80:5194–5202
Mendel G (1866) Versuche über Pflanzen-Hybriden. Verhandlungen des naturforschenden Vereins in Brünn 4:3–47
Mendel G (1870) Über einige aus künstlicher Befruchtung gewonnenen Hieracium-Bastarde. Verhandlungen des naturforschenden Vereins in Brünn 8:26–31
Mills DR, Peterson RL, Spiegelman S (1967) An extracellular Darwinian experiment with a self-duplicating nucleic acid molecule. Proc Natl Acad Sci USA 58:217–224
Moore PB (1999) Structural motifs in RNA. Annu Rev Biochem 68:287–300
Nakaishi T, Iio K, Yamamoto K, Urabe I, Yomo T (2002) Kinetic properties of Qβ replicase, an RNA dependent RNA polymerase. J Biosci Bioeng 93:322–327
Okasha S (2008) Fisher’s fundamental theorem of natural selection—a philosophical analysis. Br J Phil Sci 59:319–351
Phillipson PE, Schuster P (2009) Modeling by nonlinear differential equations. Dissipative and conservative processes. World Scientific Series on Nonlinear Science A, vol 69. World Scientific, Singapore
Price GR (1972) Fisher’s “fundamental theorem” made clear. Annals of Human Genetics 36:129–140
Reidys C, Stadler PF, Schuster P (1997) Generic properties of combinatory maps. Neutral networks of RNA secondary structure. Bull Math Biol 59:339–397
Sanger F, Nicklen S, Coulson A (1977) DNA sequencing with chain-terminating inhibitors. Proc Natl Acad Sci USA 74:5463–5467
Schultes EA, Bartel DP (2000) One sequence, two ribozymes: implications for the emergence of new ribozyme folds. Science 289:448–452
Schuster P (2003) Molecular insight into the evolution of phenotypes. In: Crutchfield JP, Schuster P (eds) Evolutionary dynamics—exploring the interplay of accident, selection, neutrality, and function, Oxford University Press, New York, pp 163–215
Schuster P (2006) Prediction of RNA secondary structures: From theory to models and real molecules. Reports on Progress in Physics 69:1419–1477
Schuster P, Swetina J (1988) Stationary mutant distribution and evolutionary optimization. Bull Math Biol 50:635–660
Schuster P, Fontana W, Stadler PF, Hofacker IL (1994) From sequences to shapes and back: a case study in RNA secondary structures. Proc R Soc Lond B 255:279–284
Seneta E (1981) Non-negative matrices and Markov chains, 2nd edn. Springer-Verlag, New York
Spiegelman S (1971) An approach to the experimental analysis of precellular evolution. Q Rev Biophys 4:213–253
Stadler BRM, Stadler PF, Wagner GP, Fontana W (2001) The topology of the possible: formal spaces underlying patterns of evolutionary change. J Theor Biol 213:241–274
Thompson CJ, McBride JL (1974) On Eigen’s theory of the self-organization of matter and the evolution of biological macromolecules. Math Biosci 21:127–142
Verhulst P (1838) Notice sur la loi que la population pursuit dans son accroisement. Corresp Math Phys 10:113–121
Weissmann C (1974) The making of a phage. FEBS Lett 40:S10–S18
Wiehe T (1997) Model dependency of error thresholds: the role of fitness functions and contrasts between the finite and infinite sites models. Genet Res Camb 69:127–136
Zuker M (1989a) On finding all suboptimal foldings of an RNA molecule. Science 244:48–52
Zuker M (1989b) The use of dynamic programming algorithms in RNA secondary structure prediction. In: Waterman MS (ed) Mathematical methods for DNA sequences, CRC Press, Boca Raton, pp 159–184
Zuker M, Stiegler P (1981) Optimal computer folding of larger RNA sequences using thermodynamics and auxiliary information. Nucl Acids Res 9:133–148
Zwillinger D (1998) Handbook of differential equations, 3rd edn. Academic Press, San Diego
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Schuster, P. Mathematical modeling of evolution. Solved and open problems. Theory Biosci. 130, 71–89 (2011). https://doi.org/10.1007/s12064-010-0110-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12064-010-0110-z