Automatic gait classification patterns in spastic hemiplegia

Abstract

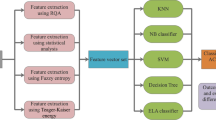
Clinical gait analysis and the interpretation of related records are a powerful tool to aid clinicians in the diagnosis, treatment and prognosis of human gait disabilities. The aim of this study is to investigate kinematic, kinetic, and electromyographic (EMG) data from child patients with spastic hemiplegia (SH) in order to discover useful patterns in human gait. Data mining techniques and classification algorithms were used to explore data from 278 SH patients. We studied different techniques for selection of attributes in order to get the best classification scores. For kinematics data, the dimension of the initial attribute space was 1033, which was reduced to 78 using the Ranker and FilteredAttributeEval algorithms. For kinetics data, the best combination of attributes was determined by SubsetSizeForward Selection and CfsSubEval with a reduction of attribute space size from 931 to 25. Decision-tree based learning algorithms, in particular the logistic model tree based on logistic regression and J48, produced the best scores for correct SH gait classification (89.393% for kinetics, 89.394% for kinematics, and 97.183% for EMG). To evaluate the effectiveness of combined feature selection methods with the classifiers, quantitative measures of model quality were used (kappa statistic, measures of sensitivity and specificity, verisimilitude rates, and ROC curves). Comparison of these results to a qualitative assessment from physicians showed a success rate of 100% for results from kinematics and EMG data, while for kinetics data the success rate was 60%. The patterns resulting from automatic data analysis of gait records have been integrated into an end-user application in order to support medical decision-making.

Annex A

1.1 Evaluator and search methods for feature selection

Feature selection can be considered as a search problem (subset generation) with some evaluation criteria (subset evaluation) including a stopping criterion (Al Janabi and Kadhim 2018). A short description of the Search and Evaluation methods is presented below. Additional details about these methods can be found in Weka (2020) and Witten et al. (2011).

1.1.1 Search methods

Search algorithms provide a way to select an optimal set of attributes. An individual attribute or a set of attributes fetched by the search algorithm is an input to the Feature Evaluator, which measures its worthiness. The starting point for these algorithms can be no/all attributes or an arbitrary point in the attribute space. The search process is stopped when the addition or deletion of any attribute results in a decrease in the evaluation or when a predetermined number of features/iterations has occurred or when an optimal subset of features is obtained (Al Janabi and Kadhim 2018). Search can also produce a ranked list of attributes by traversing the space from one side to the other and recording the order in which attributes are selected (Arun Kumar et al. 2017). Search methods that traverse the attribute space to find a good subset include (Witten et al. 2011):

• BestFirst: Searches the space of attribute subsets by greedy hill climbing augmented with a backtracking facility. It can search forward from the empty set of attributes, backward from the full set, or start at an intermediate point (specified by a list of attribute indexes) and search in both directions by considering all possible single-attribute additions and deletions. Subsets that have been evaluated are cached for efficiency.

• LinearForwardSelection: Extension of BestFirst. It limits the number of attribute expansions in each forward selection step to a restricted number (k) of attributes. At first, a specified subset evaluator is used to rank the attributes individually. Afterwards, the algorithm proceeds in two modes of operation; In the first mode, called fixed set, a forward best-first search is performed on just the k top-ranked attributes. In the second mode, called fixed width, the search considers expanding the best subset at each step by selecting an attribute from the k top-ranked attributes. The search uses either the initial ordering to select the top k attributes, or performs a ranking (with the same evaluator the search uses later on). The search direction can be forward, or floating forward selection (with optional backward search steps).

• SubsetsizeFowardSelection: Extension of LinearFowardSelection with a process to determine the optimal subset size. Performs an internal cross-validation on the training data. It applies LinearForwardSelection m times—once for each training set in the cross-validation. A given test fold is used to evaluate each size of subset explored by LinearForwardSelection in its corresponding training set. The performance for each subset size is then averaged over the folds. Finally, LinearForwardSelection is performed on all the data to find a subset of that optimal size.

• GreedyStepwise: Performs a greedy forward or backward search through the space of attribute subsets. May start with no/all attributes or from an arbitrary point in the space. Stops when the addition/deletion of any attribute results in a decrease in evaluation. Can also produce a ranked list of attributes. Like BestFirst, it may progress forward from the empty set or backward from the full set. Unlike BestFirst, it does not backtrack but terminates as soon as adding or deleting the best remaining attribute decreases the evaluation metric. In an alternative mode, it ranks attributes by traversing the space from empty to full (or vice versa) and recording the order in which attributes are selected.

• Ranker: Ranks attributes by their individual evaluations. It is not a search method for attribute subsets but rather a ranking scheme for individual attributes. It sorts attributes by their individual evaluations and must be used in conjunction with one of the single attribute evaluators—not an attribute subset evaluator. Ranker not only ranks attributes but also performs attribute selection by removing the lower-ranking ones

1.1.2 Evaluation methods

Subsets of features generated based on a certain search strategy are passed through an evaluation function, which measures the quality of the subset. The subset generated is compared with the previous best and replaces it if it is found to be better (Al Janabi and Kadhim 2018). Two commonly used techniques for evaluation are Attribute Subset Evaluator and Single-Attribute Evaluator (Witten et al. 2011). Subset evaluators take a subset of attributes and return a numerical measure that guides the search. For this, evaluators use different search algorithms to generate the feature subset and the degree of relevance is measured using different Machine Learning methods (Arun Kumar et al. 2017). Single-Attribute Evaluation uses the ranking method to measure the degree of relevance.

• Correlation-based Feature Selection (CfsSubsetEval) is an attribute subset evaluator that evaluates the worth of a subset of attributes by considering the individual predictive ability of each feature along with the degree of redundancy between them (Hall 1999). The feature subsets are ranked according to a correlation based heuristic evaluation function. The bias of the evaluation function is toward subsets that contain features that are highly correlated with the class and uncorrelated with each other. Irrelevant features should be ignored because they will have low correlation with the class. Redundant features should be screened out as they will be highly correlated with one or more of the remaining features. The acceptance of a feature will depend on the extent to which it predicts classes in areas of the instance space not already predicted by other features. The heuristic assigns high scores to subsets containing attributes that are highly correlated with the class and have low inter-correlation with each other (Hall and Holmes 2003):

  $$ Merit_{s} = \frac{{k\overline{{r_{cf} }} }}{{\sqrt {k + k\left( {k - 1} \right)\overline{{r_{ff} }} } }} $$

  where Merit_s is the heuristic ‘merit’ of a feature subset S containing k features, $\overline{{r_{cf} }}$ is the mean feature-class correlation (f ∈ S), and $\overline{{r_{cf} }}$ is the average feature–feature intercorrelation. The numerator can be thought of as providing an indication of how predictive of the class a set of features are; the denominator of how much redundancy there is among the features (Hall 1999; Hall and Holmes 2003).

• FilteredAttributeEval: is a single-attribute evaluator that applies an arbitrary evaluator to filtered data. Single-attribute evaluators are used with the Ranker search method to generate a ranked list from which Ranker discards a given number. The evaluators commonly used include (Witten et al. 2011):

  • ReliefFAttributeEval (Kira and Rendell 1992) is instance based: It samples instances randomly and checks neighboring instances of the same and different classes. It operates on discrete and continuous class data.

  • InfoGainAttributeEval (Quinlan 1986) evaluates attributes by measuring their information gain with respect to the class. It is defined as InfoGain(Class, Attribute) = H(Class) – H(Class | Attribute), where H is the information entropy.

  • ChiSquaredAttributeEval evaluates attributes by computing the Chi squared statistic with respect to the class.

  • Gain-RatioAttributeEval evaluates attributes by measuring their gain ratio with respect to the class.

  • SymmetricalUncertAttributeEval evaluates an attribute by measuring its symmetrical uncertainty with respect to the class.

  • OneRAttributeEval uses the simple accuracy measure adopted by the OneR classifier.

Classifier Algorithms

Best first tree (BFT)	Constructs a decision tree using a best-first expansion of nodes rather than the depth-first expansion used by standard decision tree learners (such as C4.5). Pre- and postpruning options are available that are based on finding the best number of expansions to use via cross-validation on the training data (Shi 2007; Friedman et al. 2000)
Functional tree (FT)	Builds functional trees (Gama 2004)—that is, trees for classification with linear functions at the leaves and, optionally, at interior nodes as well. It builds on the LMT implementation and expands the choice of attributes to split on at interior nodes by creating synthetic attributes that hold the class probabilities predicted by that node’s logistic regression model
J48	C4.5 decision tree learner (implements C4.5 release 8). The C4.5 algorithm derives from the simple divide-and-conquer algorithm for producing decision trees (Quinlan 1993). C4.5 Release 8, the last noncommercial version of C4.5, includes an MDL-based adjustment to the information gain for splits on numeric attributes
Random forest (RF)	Builds a randomized decision tree (random forests) in each iteration of the bagging algorithm (Breiman 2001)
Random tree (RT)	Constructs a tree that considers a given number of random features at each node. Performs no pruning. Also has an option to allow estimation of class probabilities (or target mean in the regression case) based on a hold-out set (backfitting) (Witten et al. 2011)
Logistic model tree (LMT)	Builds logistic model trees, which are classification trees with logistic regression functions at the leaves. When fitting these functions at a node using the LogitBoost algorithm, it uses cross-validation just once to determine how many iterations to run, and employs the same number throughout the tree instead of cross-validating at every node (Landwehr et al. 2005)
Fast decision tree learner (REPTree)	Fast tree learner that uses reduced-error pruning. Builds a decision or regression tree using information gain/variance reduction and prunes it using reduced-error pruning. It deals with missing values by splitting instances into pieces, as C4.5 does (Witten et al. 2011)
SimpleCart (SC)	Decision tree learner using CART’s minimal cost complexity pruning strategy. Named after the CART (classification and regression tree) learner that pioneered this strategy (Breiman et al. 1984)
DecisionStump (DS)	Builds one-level binary decision trees for datasets with a categorical or numeric class, dealing with missing values by treating them as a separate value and extending a third branch from the stump (Witten et al. 2011)
Hoeffding tree (HT)	An incremental, anytime decision tree induction algorithm that is capable of learning from massive data streams, assuming that the distribution generating examples does not change over time. Hoeffding trees exploit the fact that a small sample can often be enough to choose an optimal splitting attribute (Hulten et al. 2001)
RBFNetwork (RBF)	Implements a normalized Gaussian radial basis function network, deriving the centers and widths of hidden units using k-means and combining the outputs obtained from the hidden layer using logistic regression if the class is nominal, or linear regression if it is numeric (Witten et al. 2011)
Sequential minimal optimization (SMO)	Implements the sequential minimal optimization algorithm for training a support vector classifier, using kernel functions such as polynomial or Gaussian kernels (Platt 1999; Keerthi et al. 2001). For constructing a tree that considers K randomly chosen attributes at each node. Performs no pruning. Also has an option to allow estimation of class probabilities (or target mean in the regression case) based on a hold-out set (backfitting)
Multilayer Perceptron (MP)	Backpropagation neural network. It uses backpropagation to learn a multi-layer perceptron to classify instances. This network has three layers: an input layer, a hidden layer to which all the input nodes are connected; and an output. Output nodes for numeric classes are automatically converted to unthresholded linear units (Weka 2020)
Decision table (DT)	Builds a simple decision table majority classifier. It evaluates feature subsets using best-first search and can use cross-validation for evaluation (Kohavi 1995). An option uses the nearest-neighbor method to determine the class for each instance that is not covered by a decision table entry, instead of the table’s global majority, based on the same set of features
PART	Obtains rules from partial decision trees built using J48. It builds the tree using C4.5’s heuristics (Frank and Witten 1998)
ZeroR	Predicts the majority class (if nominal) or the average value (if numeric). Although there is no predictability power in ZeroR, it is useful for determining a baseline performance as a benchmark for other classification methods (Weka 2020)
ViaRegression (mVR)	Uses regression methods. Class is binarized and one regression model is built for each class value (Frank et al. 1998)
Adaptive Boosting (AdaBoostM1)	Boost using the AdaBoostM1 method (Freund and Schapire 1996). It handles weighted instances, where the weight of an instance is a positive number. The presence of instance weights changes the way in which a classifier’s error is calculated: It is the sum of the weights of the misclassified instances divided by the total weight of all instances, instead of the fraction of instances that are misclassified. By weighting instances, the learning algorithm can be forced to concentrate on a particular set of instances, namely those with high weight. Such instances become particularly important because there is a greater incentive to classify them correctly