Improvement of edge response in multi-detector row CT by high-spatial-frequency sampling of projection data | International Journal of Computer Assisted Radiology and Surgery Skip to main content
Springer Nature Link
Log in

Improvement of edge response in multi-detector row CT by high-spatial-frequency sampling of projection data

  • Original article
  • Published:
International Journal of Computer Assisted Radiology and Surgery Aims and scope Submit manuscript

Abstract

Purpose

The edge response behavior of multi-detector row computed tomography (MDCT) in high-spatial- frequency sampling may diminish due to fluctuations, so a method for improving the edge response was developed and tested.

Method

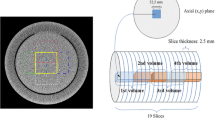
MDCT enables thin-slice and high-speed scanning compared with conventional single-detector row CT (SDCT). However, MDCT uses increased volume scanning with a simultaneous increase in the radiation dose to patients. Recently, we proposed a fluctuation reduction method using high-spatial-frequency data sampling; however, the edge response in the processed image decreased. In this research, we investigate the edge response behavior in the high-spatial-frequency sampling, and propose a method for improving the edge response. To verify this method, a large water phantom that consists of five resinous rods and a small phantom with a similitude rate of 0.5, which is topologically similar to the former large phantom were scanned, and projection data sampling using high-spatial-frequency was simulated. Thereafter, reconstructed images were obtained by averaging the high-spatial-frequency sampling data, edge gradients of profiles were calculated, and the increased rate of the gradient values were evaluated.

Results

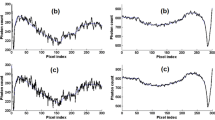
This method increased the image noise slightly and provided higher gradient values with the same image matrix size as the conventional scans could be obtained without special image processing. In this phantom study, in order to simulate the high-spatial-frequency sampling, a large phantom was scanned and the fluctuation of transmitted X-rays was increased, thereby increasing the noise.

Conclusion

A phantom study of projection data sampling by high-spatial-frequency sampling was simulated in the x- and y-direction by scanning two phantoms, and the improvement in the edge response by this method produced 25–97% improvement using double-spatial-frequency sampling. If low-noise or high-sensitivity detector is developed, this method may be more effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Endo M, Tsunoo T, Kandatsu S, Tanada S, Aradate H, Saito Y (2003) Four-dimensional Computed Tomography (4D-CT)—concepts and preliminary development. Radiat Med 21(1): 17–22

    PubMed  Google Scholar 

  2. Donoho DL (1993) Nonlinear wavelet methods for recovery of signals, densities, and spectra from indirect and noisy data. Proc Symp Appl Math 47:173–205

    Google Scholar 

  3. Donoho DL (1995) De-noising by soft-thresholding. IEEE Trans Inform Theory 41(3):613–627

    Article  Google Scholar 

  4. Reiter E (1996) Wavelet compression of medical imagery. Telemed J 2(2):131–137

    PubMed  CAS  Google Scholar 

  5. Tikkanen PE (1999) Nonlinear wavelet and wavelet packet denoising of electrocardiogram signal. Biol Cybernet 80(4):259–267

    Article  CAS  Google Scholar 

  6. Cherkassky V, Kilts S (2001) Myopotential denoising of ECG signals using wavelet thresholding methods. Neural Netw 14(8):1129–1137

    Article  PubMed  CAS  Google Scholar 

  7. Harpen MD (1999) A computer simulation of wavelet noise reduction in computed tomography. Med Phys 26(8): 1600–1606

    Article  PubMed  CAS  Google Scholar 

  8. Yasuda N, Ishikawa Y, Kodera Y (2005) Improvement of Image Quality in Chest MDCT Using Nonlinear Wavelet Shrinkage with Trimmed-thresholding. Jpn J Radiol Technol 61(12):1599–1608

    Google Scholar 

  9. Yasuda N, Abe S, Nishimura K, Sato H, Tomida T, Muraishi H, Kanai T, Tazawa S, Kawachi K (2003) Comparison of Wavelet Shrinkage and Fourier Noise Reductions in Heavy Ion Computed Tomography. In: Proceedings of the World Congress on Medical Physics and Biomedical Engineering, [CD-ROM] ISBN 1877040142

  10. Sasaki T, Hanari T, Sasaki M, Oikawa H, Gakumazawa H, Okumura M, Ikeda Y, Toyoshima N (2004) Reduction of radiation exposure in CT perfusion study using a quantum de-noising filter. Jpn J Radiol Technol 60(12):1688–1693

    Google Scholar 

  11. Daubechies I (1988) Orthogonal bases of compactly supported wavelets. Comm Pure Appl Math 41:909–996

    Google Scholar 

  12. Mallat SG (1989) A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans Pattern Anal Mach Intell 11(7):674–693

    Article  Google Scholar 

  13. Daubechies I (1990) The wavelet transform, time-frequency localization and signal analysis. IEEE Trans Inform Theory 36(5):961–1005

    Article  Google Scholar 

  14. Mallat S, Zhong S (1992) Characterization of signals from multiscale edges. IEEE Trans Pattern Anal Mach Intell 14(7):710–732

    Article  Google Scholar 

  15. Uchiyama Y, Yamamoto K (1998) Enhancement of fine structure in medical image using wavelet analysis. J Comput Aid Diagn Med Images 2(1):1–6

    Google Scholar 

  16. Petrascu O, Bel A, Linthout N, Verellen D, Soete G, Storme G (2000) Automatic on-line electronic portal image analysis with a wavelet-based edge detector. Med Phys 27(2):321–329

    Article  PubMed  CAS  Google Scholar 

  17. Laine A, Fan J, Schuler S (1994) A framework for contrast enhancement by dyadic wavelet analysis. In: Proceedings of the 2nd international workshop on digital mammography, pp 91–100

  18. Yasuda N, Ishikawa Y, Kodera Y (2006) Improvement of image quality in MDCT by high-frequency sampling of x-, y- and z-direction. In: Proceedings of the international society for optical engineering, vol 6144, pp 61446C-61441–61448

  19. Glover GH, Pelc N J (1980) Nonlinear partial volume artifacts in X-ray computed tomography. Med Phys 7:238–248

    Article  PubMed  CAS  Google Scholar 

  20. Zou Y, Sidky EY, Pan X (2004) Partial volume and aliasing artefacts in helical cone-beam CT. Phys Med Biol 49:2365–2375

    Article  PubMed  Google Scholar 

  21. Iwamoto S, Shiozaki A (2006) Statistical influence of logarithmic transform of projection data with noise and a simple correction method. (in Japanese) Med Imag Tech 24(3): 209–215

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Medical Sciences, Nagoya University, 1-1-20 Daiko-minami, Higashi-ku, Nagoya-city, Aichi, 461-8673, Japan

    Naruomi Yasuda & Yoko Ishikawa

  2. School of Health Sciences, Nagoya University, 1-1-20 Daiko-minami, Higashi-ku, Nagoya-city, Aichi, 461-8673, Japan

    Yoshie Kodera

Authors
  1. Naruomi Yasuda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yoko Ishikawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yoshie Kodera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Naruomi Yasuda.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yasuda, N., Ishikawa, Y. & Kodera, Y. Improvement of edge response in multi-detector row CT by high-spatial-frequency sampling of projection data. Int J CARS 1, 311–320 (2007). https://doi.org/10.1007/s11548-007-0067-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11548-007-0067-7

Keywords

Search

Navigation