Abstract
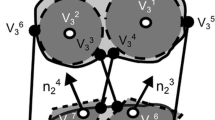
A fully automated computer algorithm for calculating the articular contact points between two bone surface models is presented. The algorithm requires the bone surface models and their relative positions as inputs in order to resolve the articular contact path. In the case of surface model overlap due to measurement errors or as a solution of an optimization procedure, the result is a volumetric estimation of the space confined between the two surfaces. The algorithm is based on attaching a grid of lines to one bone surface model and calculating the intersecting points of each of the lines in the grid with both bone surface models. The contact points are then determined as the closest points between the surfaces along the lines in the grid. The same contact points are used to evaluate any volume that is confined between two overlapping surface models. The algorithm is ideal for use in biomechanical studies, simulations of joint motion, and optimizations that require an iterative process to determine contact path and relative bone position. The algorithm is applied to a Sawbones® knee model that is moved from flexion to extension while being tracked by an optical tracking system. The contact path of the two bones is generated and an example of calculating bone impingement is provided.









Similar content being viewed by others
References
Asano T, Akagi M, Tanaka K, Tamura J, Nakamura T (2001) In vivo three dimensional knee kinematics using a biplanar image-matching techniques. Clin Orthop 388:157–166
Bansk S, Hodge WA (1996) Accurate measurement of three-dimensional knee replacement kinematics using single plane fluoroscopy. IEEE Trans Biomed Eng 43:638–649
Banks S, Markovich GD, Hodge WA (1997) In vivo kinematics of cruciate-retaining and substituting knee arthroplasties. J Arthroplasty 12:297–304
Blankevoort L, Kuiper JH, Huiskes R, Grootenboer HJ (1991) Articular contact in a three-dimensional model of the knee. J Biomech 24:1019–1031
Chen E, Ellis RE, Bryant JT, Rudan JF (2001) A computational model of postoperative knee kinematics. Med Image Anal 5:317–330
Davidson JK, Hunt KH (2004) Robots and screw theory, application of kinematics and statics to robotics. Oxford University Press, New York,
DeFrate LE, Sun H, Gill TJ, Rubash HE, Li G (2004) In vivo tibiofemoral contact analysis using 3D MRI-based knee models. J Biomech 37:1499–1504
DiGioia AM, Jaramaz B, Blackwell M, Simon DA, Fritz M, Moody JE, Nikou C, Colgan BD, Aston MA, Labaraca RS, Kischell E, Kanade T (1998) The Otto Aufrance award: image guided navigation system to measure intraoperatively acetabular implant alignment. Clin Orthop 355:8–22
Essinger JR, Leyvaraz PF, Heegard HJ, Robertson DD (1989) A mathematical model for the evaluation of the behaviour during flexion of condylar-type knee prostheses. J Biomech 22:1229–1241
Greis PE, Scuderi MG, Mohr A, Bachus KN, Burks RT (2002) Glenohumeral articular contact areas and pressures following labral and osseous injury to the anteroinferior quadrant of the glenoid. J Shoulder Elbow Surg 11:442–451
Heino BJ, Powers CM, Terk MR, Ward SR, Lee TQ (2003) Quantification of the patellofemoral joint contact area using magnetic resonance imaging. Magn Reson Imaging 21:955–959
Hoff WA, Komistek RD, Dennis DA, Gabriel SM, Walker SA (1996) Three-dimensional determination of femoral–tibial contact positions under “in vivo” conditions using fluoroscopy. In: Proceedings of the European society of biomechanics, Leuven, pp 28–31
Hsieh YF, Draganich LF, Ho SH, Reider B (2002) The effect of removal and reconstruction of the anterior cruciate ligament on the contact characteristics of the patellofemoral joint. Am J Sports Med 30:121–127
Huberti HH, Hayes WC (1984) Patellofemoral contact pressures. The influence of q-angle and tendofemoral contact. J Joint Bone Surg A 66:715–724
Invaco SJ, Mullins E, Coughlin KM, Banks S, Banks A, Beynnon BD (2004) Tibiofemoral kinematic analysis of kneeling after total knee arthroplasty. J Arthroplasty 19:906–910
Klein F (1871) Ueber Liniengeometrie und metrische Geometrie. Mathematische Annalen v, pp 257–303
Komistek RD, Scott RD, Dennis DA, Yasgur D, Anderson DT, Hajner ME (2002) In vivo comparison of femorotibial contact positions for press fit posterior stabilized and posterior cruciate-retaining total knee arthroplasties. J Arthroplasty 17:209–216
Komistek RD, Dennis DA, Mahfouz M (2003) In vivo fluoroscopic analysis of the normal human knee. Clin Orthop 410:69–81
Pottmann H, Wallner J (2001) Computational line geometry. Springer, Berlin
Pottmann H, Peternell M, Ravani B (1999) An introduction to line geometry with applications. Comput Aided Des 31:3–16
Scarvell JM, Smith PN, Refshauge KM, Galloway HR, Woods KR (2004) Evaluation of a method to map tibiofemoral contact points in the normal knee using MRI. J Orthop Res 22:788–793
Tsai LW (1999) Robot analysis: the mechanics of serial and parallel manipulators. Wiley, New York
Von Eisenhart-Rothe R, Siebert M, Bringmann C, Vogl T, Englmeier KH, Graichen H (2004) A new in vivo technique for determination of 3D kinematics and contact areas of the patello-femoral and tibio-femoral joint. J Biomech 37:927–934ssss
Wilson DR, Apreleva MV, Eichler MJ, Harrold FR (2003) Accuracy and repeatability of the pressure measurement system in the patellofemoral joint. J Biomech 36:1909–1915
Wismans J, Veldpaus F, Janssen J (1980) A three-dimensional mathematical model of the knee-joint. J Biomech 13:677–685
Acknowledgments
This work was supported by the National Science Foundation of the United States under NSF ITR Grant No. 0325920.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wolf, A., Jaramaz, B. & Murtha, P.E. Fully automated computer algorithm for calculating articular contact points with application to knee biomechanics. Med Biol Eng Comput 46, 233–240 (2008). https://doi.org/10.1007/s11517-007-0297-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-007-0297-4