Modeling of skeletal muscle: the influence of tendon and aponeuroses compliance on the force–length relationship | Medical & Biological Engineering & Computing Skip to main content
Springer Nature Link
Log in

Modeling of skeletal muscle: the influence of tendon and aponeuroses compliance on the force–length relationship

  • Original Article
  • Published:
Medical & Biological Engineering & Computing Aims and scope Submit manuscript

Abstract

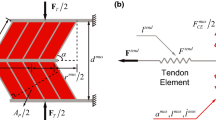
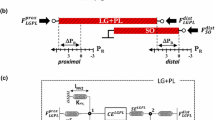
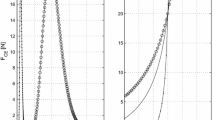
The aim of this study was to investigate the influence of changing elastic properties of tendon and aponeuroses on force production and muscle geometry. A three-dimensional, structural, continuum mechanics model of the cat medial gastrocnemius was used for this purpose. Increasing compliance in tendon and aponeuroses caused a decrease in the peak isometric force and a shift of the force–length relationship to the right of the length axis (i.e. toward greater muscle lengths). This result can be explained with the stability condition of the force–length relationship which produced a history dependence of force production that is conceptually in agreement with experimental observations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Chadwick P (1999) Continuum mechanics concise theory and problems. Dover Publications, New York

    Google Scholar 

  2. Corr D, Herzog W (2005) Force recovery following activated shortening in whole skeletal muscle: transient and steady-state aspects of force depression. J Appl Phys 99:252–260. doi:10.1152/japplphysiol.00509

    Article  Google Scholar 

  3. Edman K, Elzinga G, Noble M (1982) Residual force enhancement after stretch of contracting frog single muscle fibers. J Gen Physiol 80:769–784

    Article  Google Scholar 

  4. Epstein M, Herzog W (1998) Theoretical models of skeletal muscle. Wiley, Chichester

    Google Scholar 

  5. Epstein M, Herzog W (2003) Aspects of skeletal muscle modelling. Proc R Soc 358:1445–1452. doi:10.1098/rstb.2003.1344

    Google Scholar 

  6. Fernandez JW, Mithraratne P, Thrupp SF, Tawhai MH, Hunter PJ (2002) Anatomically based geometric modelling of the musculo-skeletal system and other organs. Biomech Model Mechanobiol 2:139–155. doi:10.1007/s10237-003-0036-1

    Article  Google Scholar 

  7. Gans C, Bock CW (1965) The functional significance of muscle architecture: a theoretical analysis. Ergebn Anat Entw Gesch 38:115–142

    Google Scholar 

  8. Gielen AWJ, Oomens CWJ, Bovendeerd PHM, Arts T, Janssen JD (2000) A finite element approach for skeletal muscle using a distributed moment model of contraction. Comp Meth Biomech Biomed Eng 3:231–244

    Article  Google Scholar 

  9. Gordon AM, Huxley AF, Julian FJ (1966) The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J Physiol 184:170–192

    Google Scholar 

  10. Griffiths RI (1987) Ultrasound transit time gives direct measurement of muscle fiber length in vivo. J Neurosci Meth 21:159–165

    Article  Google Scholar 

  11. Herzog W (2005) Force enhancement following stretching of activated muscle: critical review and proposal for mechanisms. Med Biol Eng Comput 43:173–180. doi:10.1007/BF02345951

    Article  Google Scholar 

  12. Hill A (1938) The heat of shortening and the dynamic constants of muscle. Proc R Soc 126:136–195

    Google Scholar 

  13. Hunter PJ, Smaill BH (1988) The analysis of cardiac function: a continnum approach. Prog Biophys Mol Biol, pp 101–164

  14. Huxley A (1957) Muscle structure and theories of contraction. Prog Biophys Biophys Chem 7:255–318

    Google Scholar 

  15. Kaya M, Carvalho W, Leonard T, Herzog W (2002) Estimation of cat medial gastrocnemius fascicles lengths during dynamic contractions. J Biomech 35:893–902

    Article  Google Scholar 

  16. Lemos RR, Epstein M, Herzog W, Wyvill B (2004) A framework for structured modeling of skeletal muscle. Comp Meth Biomech Biomed Eng 7:305–317. doi:10.1080/10255840412331317398

    Article  Google Scholar 

  17. Lieber RL, Fridén J (2000) Functional and clinical significance of skeletal muscle architecture. Muscle Nerve 23:1647–1666. doi:10.1002/1097-4598(200011)23:11<1647::AID-MUS1>3.0.CO;2-M

    Article  Google Scholar 

  18. Maurel W, Wu Y, Thalmann NM, Thalmann D (1998) Biomechanical models for soft tissue simulation. Springer, Berlin

    Google Scholar 

  19. Ogden RW (1984) Non-linear elastic deformations. Dover Publications, New York

    Google Scholar 

  20. Oomens CWJ, Maenhout M, van Oijen CH, Drost MR, Baaijens FP (2003) Finite element modelling of contracting skeletal muscle. Proc R Soc 358:1453–1460. doi:10.1098/rstb.2003.1345

    Google Scholar 

  21. Sasaki N, Odajima S (1996) Elongation mechanism of collagen fibrils and force–strain relations of tendon at each level of structural hierarchy. J Biomech 29:1131–1136

    Article  Google Scholar 

  22. Schachar R, Herzog W, Leonard T (2002) Force enhancement above the initial isometric force on the descending limb of the force–length relationship. J Biomech 35:1299–1306

    Article  Google Scholar 

  23. Schroeder WJ, Avila LS, Hoffman W (2000) Visualizing with vtk: a tutorial. IEEE Comput Graph Appl 20(5):20–27

    Article  Google Scholar 

  24. Scott SH, Loeb GE (1995) Mechanical properties of aponeurosis and tendon of the cat soleus muscle during whole muscle isometric contractions. J Morphol 224:73–86. doi:10.1002/jmor.1052240109

    Article  Google Scholar 

  25. Stouffer DC, Butler DL, Hosny D (1985) The relationship between crimp pattern and mechanical response of human patellar tendon-bone units. J Biomech Eng 107:158–165

    Article  Google Scholar 

  26. Winters JM, Stark L (1987) Muscle models: what is gained and what is lost by varying model complexity. Biol Cybern 55:403–420

    Article  MathSciNet  Google Scholar 

  27. Wu JZ, Herzog W (1999) Modelling concentric contraction of muscle using an improved cross-bridge model. J Biomech 32:837–848

    Article  Google Scholar 

  28. Yucesoy CA, Koopman BHFJM, Huijing PA, Grootenboer HJ (2002) Three-dimensional finite element modeling of skeletal muscle using a two-domain approach: linked fiber-matrix mesh model. J Biomech 35(9):1253–1262

    Article  Google Scholar 

  29. Zahalak G (1981) A distribution-moment approximation for kinetic theories of muscular contraction. Math Biosci 55:89–114

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported in part by CAPES-Brazil, University of Caxias do Sul, FAPERGS, University of Calgary, NSERC of Canada, and The Canada Research Chair Programme.

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Caxias do Sul, Caixa Postal 1352, 95020-972, Caxias do Sul, RS, Brazil

    R. R. Lemos

  2. Department of Mechanical and Manufacturing Engineering, University of Calgary, Calgary, AB, Canada

    M. Epstein

  3. Faculty of Kinesiology, University of Calgary, Calgary, AB, Canada

    W. Herzog

Authors
  1. R. R. Lemos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Epstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. W. Herzog
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. R. Lemos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lemos, R.R., Epstein, M. & Herzog, W. Modeling of skeletal muscle: the influence of tendon and aponeuroses compliance on the force–length relationship. Med Bio Eng Comput 46, 23–32 (2008). https://doi.org/10.1007/s11517-007-0259-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11517-007-0259-x

Keywords

Search

Navigation