Performance Analysis of Downlink-NOMA Over Málaga Distributed Optical Links

Abstract

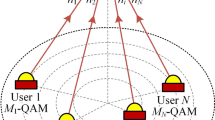
Non-orthogonal multiple access (NOMA) can be a desirable method since it can utilize resources efficiently to provide larger capacity. Similarly, optical transmission is also becoming popular due to the availability of licence-free large bandwidth and low-cost transceiver implementation. Although optical NOMA system can be promising for long range wireless systems, investigation of its reliability performance is essential for different channel models. In this study, outage probability, channel capacity, symbol error rate expressions, diversity and coding gains for arbitrary number of users are obtained for downlink-NOMA over free space optical links modeled with Málaga distribution. Theoretical results are verified by numerical examples for various scenarios providing useful background for future analyses and designs.

Appendices

Appendix A: Derivation of PDF of SINR

Three steps to obtain the PDF of $\gamma$ in (7) contain the derivations of PDFs for $\frac{\delta }{\lambda }$, $\frac{\delta }{\lambda }+\varrho$ and $\frac{\kappa }{\frac{\delta }{\lambda }+\varrho }$. In the first stage, it is required that PDF of $\frac{\delta }{\lambda }$ must be evaluated by using the PDF of $\lambda$ (i.e. channel gain=$I^2$) which can be easily obtained as below,

$$\begin{aligned} f_{\lambda }(\lambda )=\frac{A}{2}\displaystyle \sum _{k=1}^{\beta }a_k\lambda ^{\frac{\alpha +k}{4}-1} K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{\lambda }}\bigg ), \end{aligned}$$

(A1)

where $\zeta =\frac{\alpha \beta }{\eta \beta +\Omega '}$. The PDF of $\tau =\frac{\delta }{\lambda }$ can be found via CDF of $\lambda$ in (A1). The CDF of $\tau$ is $F_{\tau }(\tau )=1-Pr(0\le \lambda \le \frac{\delta }{\tau })$, then

$$\begin{aligned} F_{\tau }(\tau )=1-\int _{\lambda =0}^{\frac{\delta }{\tau }}f_{\lambda }(\lambda )d\lambda =1-F_{\lambda }\bigg (\frac{\delta }{\tau }\bigg ). \end{aligned}$$

(A2)

When derivatives of both sides in (A2) are computed, one can get $f_{\tau }(\tau )=\frac{\delta }{\tau ^2}f_{\lambda }(\frac{\delta }{\tau })$. By substituting $\frac{\delta }{\tau }$ into (A1), $f_{\tau }(\tau )$ is found as,

$$\begin{aligned} f_{\tau }(\tau )=\frac{A\delta }{2\tau ^2}\displaystyle \sum _{k=1}^{\beta }a_k\bigg (\frac{\delta }{\tau }\bigg )^{\frac{\alpha +k}{4}-1}K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{\frac{\delta }{\tau }}}\bigg ). \end{aligned}$$

(A3)

(6) can be rewritten as $\gamma =\frac{\kappa }{\tau +\varrho }$. Considering $\psi =\tau +\varrho$ and by using the CDF such that $F_{\psi }(\psi )=Pr(\tau +\varrho \le \psi )\hspace{2pt}\Longrightarrow \hspace{2pt}F_{\psi }(\psi ) =Pr(0\le \tau \le \psi -\varrho )=F_{\tau }(\psi -\varrho )$. It is evident that after derivative of $F_{\tau }(\psi -\varrho )$ is evaluated, $f_{\psi }(\psi )$ can be found as,

$$\begin{aligned} f_{\psi }(\psi )=\frac{A\delta }{2(\psi -\varrho )^2}\displaystyle \sum _{k=1}^{\beta }a_k\bigg (\frac{\delta }{\psi -\varrho }\bigg )^{\frac{\alpha +k}{4}-1}K_{\alpha -k} \bigg (2\sqrt{\zeta \sqrt{\frac{\delta }{\psi -\varrho }}}\bigg ). \end{aligned}$$

(A4)

(6) becomes $\gamma =\frac{\kappa }{\psi }$. PDF of $\gamma$ can be obtained from $F_{\gamma }(\gamma )=Pr(\frac{\kappa }{\psi }\le \gamma )\hspace{2pt}\Longrightarrow \hspace{2pt} F_{\gamma }(\gamma )=1-Pr(\varrho \le \psi \le \frac{\kappa }{\gamma })$ as follows,

$$\begin{aligned} f_{\gamma }(\gamma )=\frac{\kappa }{\gamma ^2}\frac{A\delta }{2(\frac{\kappa }{\gamma }-\varrho )^2} \displaystyle \sum _{k=1}^{\beta }a_k\bigg (\frac{\delta }{\frac{\kappa }{\gamma }-\varrho }\bigg )^{\frac{\alpha +k}{4}-1} K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{\frac{\delta }{\frac{\kappa }{\gamma }-\varrho }}}\bigg ). \end{aligned}$$

(A5)

Boundary values of $\gamma$ are computed as $0\le \gamma \le \frac{\kappa }{\varrho }$. When (A5) is rearranged, (7) can be obtained.

Appendix B: PDF Parameters of Normalized SINR

In this section, derivations of the PDF of normalized SINR and the parameters a and t [57] (needed for diversity and coding gains) are presented. The term $(\sqrt{\sqrt{\chi }})^{\alpha +k-4}K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{\chi }}\bigg )$ in (15) is multiplied with $\frac{(2\sqrt{\zeta })^{\alpha +k-4}}{(2\sqrt{\zeta })^{\alpha +k-4}}$ in order to write it in terms of Meijer’s G-function [55, Section 2.6]. Then, it can be rewritten as,

$$\begin{aligned} \bigg (2\sqrt{\zeta \sqrt{\chi }}\bigg )^{\alpha +k-4}K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{\chi }}\bigg ) =2^{\alpha +k-5}G_{0,2}^{2,0}\bigg (\zeta \sqrt{\chi }| _{\alpha -2,\;\;\;k-2}\bigg ). \end{aligned}$$

(B6)

When (B6) is substituted into (15), it can be written as,

$$\begin{aligned} f_{\chi }(\chi )=\frac{A}{4}\displaystyle \sum _{k=1}^{\beta }a_k\frac{1}{(\sqrt{\zeta })^{\alpha +k-4}} G_{0,2}^{2,0}\bigg (\zeta \sqrt{\chi }| _{\alpha -2,\;\;\;k-2}\bigg ). \end{aligned}$$

(B7)

Meijer’s G-function in (B7) can be written as follows ( [55, Theorem 1.4.3, Eq. (1.4.14)]) where z, q, p, $a_p$ and $b_q$ correspond to $\zeta \sqrt{\chi }$, 2, 0, $(-,\hspace{10pt}{-})$ and $({\alpha -2,\hspace{10pt} k-2})$, respectively.

$$\begin{aligned} G_{p,q}^{q,0}(z\vert ^{a_p}_{b_q})\sim {H_{p,q}(z)}=[e^{(p-q)z^{\frac{1}{q-p}}}]z^{\rho ^{*}} \bigg [\frac{(2\pi )^{\frac{q-p-1}{2}}}{(q-p)^{\frac{1}{2}}}+\frac{M_1}{z^{\frac{1}{q-p}}}+\frac{M_2}{z^{\frac{1}{q-p}}}+...\bigg ], \end{aligned}$$

(B8)

$$\begin{aligned} \rho ^{*}=\frac{1}{q-p}\bigg [\sum _{j=1}^{q}{b_j}-\sum _{j=1}^{p}{a_j}+\frac{p-q+1}{2}\bigg ]. \end{aligned}$$

(B9)

When $p=0$ and $q=2$ are substituted into Eqs. (B8) and (B9), they become $G_{0,2}^{2,0}(z|^{a_p}_{b_q})\sim [e^{-2\sqrt{z}}]z^{\rho ^{*}}\bigg [\pi ^{\frac{1}{2}} +\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]$ and $\rho ^{*}=\frac{1}{2}[\alpha +k-\frac{9}{2}]$. The term $e^{-2\sqrt{z}}$ can be expanded Maclaurin series as below,

$$\begin{aligned} & G_{0,2}^{2,0}(z|^{a_p}_{b_q})\sim \bigg [1+\sum _{i=1}^{\infty }{\frac{(-2\sqrt{z})^i}{i!}}\bigg ] z^{\rho ^{*}}\bigg [\pi ^{\frac{1}{2}}+\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ], \end{aligned}$$

(B10)

$$\begin{aligned} & \quad \begin{aligned}&G_{0,2}^{2,0}(z\vert ^{a_p}_{b_q})\sim {z^{\rho ^*}\pi ^{\frac{1}{2}}}+z^{\rho ^*}\bigg [\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]\\&\hspace{10pt}+z^{\rho ^*}\sum _{i=1}^{\infty }{\frac{(-2\sqrt{z})^i}{i!}}\bigg [\pi ^{\frac{1}{2}} +\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]. \end{aligned} \end{aligned}$$

(B11)

The result obtained by substituting (B11) into (B7) can matches with (16) as below,

$$\begin{aligned} \begin{aligned} f_{\chi }(\chi )=&a\chi ^t+o(\chi ^t)\sim \frac{A}{4}\displaystyle \sum _{k=1}^{\beta } a_k\frac{1}{(\sqrt{\zeta })^{\alpha +k-4}}\bigg [{z^{\rho ^*}\pi ^{\frac{1}{2}}}+z^{\rho ^*}\bigg [\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]\\&+z^{\rho ^*}\sum _{i=1}^{\infty }{\frac{(-2\sqrt{z})^i}{i!}}\bigg [\pi ^{\frac{1}{2}} +\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]\bigg ], \end{aligned} \end{aligned}$$

(B12)

where

$$\begin{aligned} \begin{aligned} o(\chi ^t)=&\frac{A}{4}\displaystyle \sum _{k=1}^{\beta }a_k\frac{1}{(\sqrt{\zeta })^{\alpha +k-4}} \bigg [z^{\rho ^*}\bigg [\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]\\&+z^{\rho ^*}\sum _{i=1}^{\infty }{\frac{(-2\sqrt{z})^i}{i!}}\bigg [\pi ^{\frac{1}{2}} +\frac{M_1}{z^{\frac{1}{2}}}+\frac{M_2}{z^{\frac{1}{2}}}+...\bigg ]\bigg ], \end{aligned} \end{aligned}$$

(B13)

and

$$\begin{aligned} \begin{aligned} a\chi ^t= & \frac{A}{4}\displaystyle \sum _{k=1}^{\beta }a_k\frac{1}{(\sqrt{\zeta })^{\alpha +k-4}}z^{\rho ^*}\pi ^{\frac{1}{2}}\\= & \frac{A}{4}\displaystyle \sum _{k=1}^{\beta }a_k\frac{1}{(\sqrt{\zeta })^{\alpha +k-4}} (\zeta \sqrt{\chi })^{\frac{1}{2}[\alpha +k-\frac{9}{2}]}\pi ^{\frac{1}{2}}=\frac{A\pi ^{\frac{1}{2}}}{4\zeta ^{\frac{1}{4}}}\displaystyle \sum _{k=1}^{\beta }a_k\chi ^{\frac{1}{4}[\alpha +k-\frac{9}{2}]}, \end{aligned} \end{aligned}$$

(B14)

which eventually offers to obtain $t=\frac{1}{4}[\alpha +k-\frac{9}{2}]$, $a=\frac{A\pi ^{\frac{1}{2}}}{4\zeta ^{\frac{1}{4}}}a_k$ for only part of the summation in (B14).

Appendix C: Proof of Derivation of Average Channel Capacity

Derivation of the integral in (24) starts with the change of variables as $x=\frac{\delta \gamma }{\kappa -\gamma \varrho }$, $dx=\frac{\delta \kappa }{(\kappa -\gamma \varrho )^2}d_{\gamma }$ in that integral. Then, new parameters are substituted in (24) and it becomes as below by making some simple mathematical manipulations,

$$\begin{aligned} \frac{1}{(2\zeta )^{\frac{\alpha +k-4}{2}}}\int _{\gamma =0}^{\infty }ln \bigg (\frac{x(\varrho +\kappa )+\delta }{x\varrho +\delta }\bigg ) \bigg (2\sqrt{\zeta \sqrt{x}}\bigg )^{\alpha +k-4}K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{x}}\bigg )dx. \end{aligned}$$

(C15)

The term $\bigg (2\sqrt{\zeta \sqrt{x}}\bigg )^{\alpha +k-4}K_{\alpha -k}\bigg (2\sqrt{\zeta \sqrt{x}}\bigg )$ in (C15) can be expressed in terms of Meijer’s G-function [55, Section 2.6] and thus AVC becomes,

$$\begin{aligned} \frac{1}{2\zeta ^{\frac{\alpha +k-4}{2}}}\int _{x=0}^{\infty }ln \bigg (\frac{x(\varrho +\kappa )+\delta }{x\varrho +\delta }\bigg )G_{0,2}^{2,0} \bigg (\zeta \sqrt{x}\bigg | _{\alpha -2,\;\;k-2}\bigg )dx. \end{aligned}$$

(C16)

Using the partial integration by changing variables as $u=ln\bigg (\frac{x(\varrho +\kappa )+\delta }{x\varrho +\delta }\bigg )$ and $dv=G_{0,2}^{2,0}\bigg (\zeta \sqrt{x}\bigg | _{\alpha -2,\;\;k-2}\bigg )dx$ with $du=\bigg (\frac{1}{x+\frac{\delta }{\kappa +\varrho }}-\frac{1}{x+\frac{\delta }{\varrho }}\bigg )dx$, $v=G_{1,3}^{2,1}\bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]$ obtained based on [56], one can obtain the following equation,

$$\begin{aligned} \begin{aligned}&\int _{x=0}^{\infty }ln\bigg (\frac{x(\varrho +\kappa )+\delta }{x\varrho +\delta }\bigg )G_{0,2}^{2,0} \bigg (\zeta \sqrt{x}\bigg | _{\alpha -2,\;\;k-2}\bigg )dx=[uv]_{x=0}^{\infty }-\int _{x=0}^{\infty }vdu\\&=\bigg [ln\bigg (\frac{x(\varrho +\kappa )+\delta }{x\varrho +\delta }\bigg )G_{1,3}^{2,1}\bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]\bigg ]_{x=0}^{\infty }\\&\hspace{10pt}-\int _{x=0}^{\infty }G_{1,3}^{2,1}\bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ] \bigg (\frac{1}{x+\frac{\delta }{\kappa +\varrho }}-\frac{1}{x+\frac{\delta }{\varrho }}\bigg )dx, \end{aligned} \end{aligned}$$

(C17)

where $[uv]_{x=0}^{\infty }=ln\bigg (1+\frac{\kappa }{\varrho }\bigg )G_{1,3}^{2,1} \bigg [\infty \bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]$ and the term $G_{1,3}^{2,1}\bigg [\infty \bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]$ converges to zero when variable x goes to infinity. Therefore, $[uv]_{x=0}^{\infty }=ln\bigg (1+\frac{\kappa }{\varrho }\bigg )G_{1,3}^{2,1}\bigg [\infty \bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]=0$. Another change of variables in (C17) as $\beta _{1}=\frac{\delta }{\kappa +\varrho }$, $\beta _{2}=\frac{\delta }{\varrho }$ can be helpful in simplification as follows,

$$\begin{aligned} \begin{aligned} \int _{x=0}^{\infty }vdu= & \int _{x=0}^{\infty }\frac{1}{x+\beta _{1}}G_{1,3}^{2,1} \bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]dx\\&-\int _{x=0}^{\infty }\frac{1}{x+\beta _{2}}G_{1,3}^{2,1} \bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]dx. \end{aligned} \end{aligned}$$

(C18)

Integral in [55, Eq. 3.3.5a] is as follows,

$$\begin{aligned} \begin{aligned}&\int _{x=0}^{\infty }x^{\sigma -1}(\omega +x)^{\psi -1}G_{p,q}^{m,n} \bigg [\zeta {x}^{\frac{s}{r}}\bigg |^{a_p}_{b_q}\bigg ]dx\\&=\frac{\omega ^{\psi +\sigma -1}}{\Gamma (1-\psi )}(2\pi )^{1-s+c^*(1-r)}r^Us^{-\psi } G_{pr+s,qr+s}^{mr+s,nr+s}\bigg [\frac{\zeta ^rr^{r(p-q)}}{\omega ^s}\bigg |^{\Delta (s,1-\sigma ), \Delta (r,a_p)}_{\Delta (s,1-\psi -\sigma ), \Delta (r,b_q)}\bigg ], \end{aligned} \end{aligned}$$

(C19)

where $c^*=m+n-\frac{p}{2}-\frac{q}{2}$ and $U=\displaystyle \sum _{j=1}^{q}b_j-\displaystyle \sum _{j=1}^{p}a_j+\frac{p}{2}-\frac{q}{2}+1$. $\Delta (n,y)$ represents the set of n parameters [55, Page 70] $\frac{y}{n}, \frac{y+1}{n},...,\frac{y+n-1}{n}$. When $\sigma , \psi , s, r$ in [55, Eq. 3.3.5a] are selected as $\sigma =1$, $\psi =0$, $s=1$, $r=2$; then the both of integrals in (C18) can be put into form of integral in (C19).

When integral $\int _{x=0}^{\infty }\frac{1}{x+\beta _{1}}G_{1,3}^{2,1}\bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]dx$ and integral [55, Eq. 3.3.5a] are compared, $\sigma =1$, $\omega =\beta _1$, $\psi =0$, $m=2$, $n=1$, $p=1$, $\zeta =\zeta$, $s=1$, $r=2$, $a_p=\{1\}$, $b_q=\{\alpha -1, k-1, 0\}$. Based on this, $c^*=1$, $U=\alpha +k-3$, $\Delta (r,a_p)=\Delta (2,\{1\})$ and $\Delta (r,b_q)=\Delta (2,\{\alpha -1,k-1,0\})$.

Identity for $\Delta (.)$ is given as $\Delta (r,\{y_1, y_2,...,y_n\})\overset{\Delta }{=}\Delta (r,y_1), \Delta (r,y_2),...,\Delta (r,y_n)$ in [55, Page 117]. Based on that identity, $\Delta (2,\{\alpha -1,k-1,0\})=\Delta (2,\alpha -1),\Delta (2,k-1),\Delta (2,0)$. Finally, expanded forms of $\Delta (.)$’s are written as $\Delta (1,\{0\})=\{0\}$, $\Delta (2,\{1\})=\{\frac{1}{2}, 1\}$, $\Delta (2,\alpha -1)=\{\frac{\alpha -1}{2}, \frac{\alpha }{2}\}$, $\Delta (2,k-1)=\{\frac{k-1}{2}, \frac{k}{2}\}$, $\Delta (2,0)=\{0, \frac{1}{2}\}$. It is known that $\Gamma (1)=1$. When all parameters and $\Delta (.)$’s are substituted into (C19), one of integrals can be rewritten as,

$$\begin{aligned} \begin{aligned}&\int _{x=0}^{\infty }\frac{1}{x+\beta _{1}}G_{1,3}^{2,1} \bigg [\zeta \sqrt{x}\bigg |^{1,\;\; }_{\alpha -1,\;\;k-1,\;\;0\;\;}\bigg ]dx\\&=\frac{2^{\alpha +k-4}}{\pi }G_{3,7}^{5,3} \bigg [\frac{\zeta ^2}{16\beta _1}\bigg |^{\{0, \frac{1}{2}, 1\},\{\}}_{\{0,\frac{\alpha -1}{2}, \frac{\alpha }{2}, \frac{k-1}{2}, \frac{k}{2}\}, \{0, \frac{1}{2}\}}\bigg ]. \end{aligned} \end{aligned}$$

(C20)

Result in (C20) is also valid for integral including $\beta _2$ in (C18). Because, only different between integrals in (C18) is $\beta _1$ and $\beta _2$. Finally, when (C20) (i.e. $\int _{x=0}^{\infty }vdu$) is substituted into (C17), it can be rewritten as follows,

$$\begin{aligned} \begin{aligned} \frac{2^{\alpha +k-4}}{2\pi \zeta ^{\frac{\alpha +k-4}{2}}}\\ \times \bigg (G_{3,7}^{5,3}\bigg [\frac{\zeta ^2(\kappa +\varrho )}{16\delta }\bigg |^ {\{0, \frac{1}{2}, 1\},\{\}}_{\{0,\frac{\alpha -1}{2}, \frac{\alpha }{2}, \frac{k-1}{2}, \frac{k}{2}\}, \{0, \frac{1}{2}\}}\bigg ]-G_{3,7}^{5,3} \bigg [\frac{\zeta ^2\varrho }{16\delta }\bigg |^{\{0, \frac{1}{2}, 1\},\{\}}_{\{0,\frac{\alpha -1}{2}, \frac{\alpha }{2}, \frac{k-1}{2}, \frac{k}{2}\}, \{0, \frac{1}{2}\}}\bigg ]\bigg ). \end{aligned} \end{aligned}$$

(C21)