Impact of user mobility on wireless powered network for AF and DF relaying over FTR fading channel

Abstract

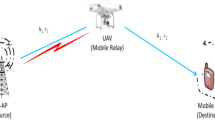
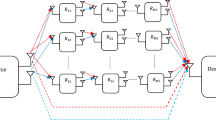
User mobility causes a significant impact on wireless system performance specifically when cell radius is small like in mm-wave band communication. This research studies, the ergodic outage probability (EOP) performance of wireless power transfer based simultaneous wireless information and power transfer system considering the random way point distributed user mobility. The fluctuating two ray fading model has been used to characterize source to relay and relay to mobile user channel, as it gives the best fit for small-scale fading measurement at the 28 GHz band and can be used to model various conventional and non-conventional fading environments. Closed form expressions for EOP have been derived for all four cases considering amplify-and-forward time switching relaying and decode-and-forward TSR protocols for no diversity and with multiple antenna reception case. Further the asymptotic expressions are also presented to get a better insight on the derived analytical expressions. The system EOP performance have been studied considering user mobility in 1D, 2D, and 3D deployment and results shows that a minute variation in node positioning can impact the system outage performance significantly. Hence the derived performances metric are useful to accurately characterize the system performance with random user mobility. Finally the accuracy of derived expressions has been validated through Monte Carlo simulations.

Appendices

Appendix 1: closed form for integral $I_{1}$

A generalised form for integral $I_{1}$ in (27) can be represented in (54)

$$I_{1} = \int\limits_{0}^{{R_{2} }} {r_{2}^{\rho_{l} } \int\limits_{\chi }^{\infty } {z^{{j_{1} }} \,e^{ - \alpha z} } } \Upsilon \left( {j_{2} + 1,\beta \frac{{r_{2}^{\varepsilon } }}{z}} \right)dzdr_{2}$$

(54)

Now changing order of integral and using transformation $r_{2}^{\varepsilon } = R_{2}^{\varepsilon } x$ we get,

$$I_{1} = \frac{{R_{2}^{\rho_l + 1} }}{\varepsilon }\int\limits_{\chi }^{\infty } {z^{{j_{1} }} e^{ - \alpha z} } \int\limits_{0}^{1} {x^{w - 1} } \Upsilon \left( {j_{2} + 1,\frac{{\beta R_{2}^{\varepsilon } }}{z}x} \right)dxdz$$

(55)

where $w = {{\left( {\rho_l + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\rho + 1} \right)} \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }$.

Using integration by part it can be shown that

$$\int\limits_{0}^{1} {x^{w - 1} \Upsilon \left( {m,ax} \right)dx = w^{ - 1} \left[ {\Upsilon \left( {m,a} \right) - a^{ - w} \Upsilon \left( {w + m,a} \right)} \right]}$$

(56)

Hence from (55) and (56),

$$\begin{aligned} I_{1} & = \frac{{R_{2}^{\rho_l + 1} }}{\varepsilon w}\underbrace {{\int\limits_{\chi }^{\infty } {z^{{j_{1} }} e^{\alpha z} } \Upsilon \left( {j_{2} + 1,\frac{{\beta R_{2}^{\varepsilon } }}{z}} \right)dz}}_{{I_{2} }} \\ & \quad - \left( {\beta R_{2}^{\varepsilon } } \right)^{ - w} \frac{{R_{2}^{\rho_l + 1} }}{\varepsilon w}\underbrace {{\int\limits_{\chi }^{\infty } {z^{{j_{1} + w}} e^{ - \alpha z} } \Upsilon \left( {w + j_{2} + 1,\frac{{\beta R_{2}^{\varepsilon } }}{z}} \right)dz}}_{{I_{3} }} \\ \end{aligned}$$

(57)

Observed that a closed form expression for integral $I_{1}$ can be obtained by solving integral $I_{2}$ and $I_{3}$. Let’s define integral $I_{2}$ as function $f\left( {j_{1} ,\left\lceil {j_{2} + 1} \right\rceil } \right)$ defined as follows,

$$f\left( {j_{1} ,\left\lceil {j_{2} + 1} \right\rceil } \right) = \int\limits_{\chi }^{\infty } {z^{{j_{1} }} \,e^{ - \alpha z} } \Upsilon \left( {j_{2} + 1,\frac{{\beta R_{2}^{\varepsilon } }}{z}} \right)dz$$

(58)

Expand incomplete gamma function using [30, 8.352.6]

$$f\left( {j_{1} ,\left\lceil {j_{2} + 1} \right\rceil } \right) = \Gamma \left( {j_{2} + 1} \right)\left[ {\int\limits_{\chi }^{\infty } {z^{{j_{1} }} e^{ - \alpha z} } dz - \sum\limits_{n = 0}^{{\left\lceil {j_{2} } \right\rceil }} {\frac{{\left( {\beta R_{2}^{\varepsilon } } \right)^{n} }}{n!}} \int\limits_{\chi }^{\infty } {z^{{j_{1} - n}} e^{{ - \alpha z - \frac{{\beta R_{2}^{\varepsilon } }}{z}}} } dz} \right]$$

(59)

With the aid of [30, 3.351.2] and [31, Eq. 14] a closed for integrals is obtained in (60)

$$\begin{gathered} f\left( {j_{1} ,\left\lceil {j_{2} + 1} \right\rceil } \right) = \frac{{\Gamma \left( {j_{2} + 1} \right)\Gamma \left( {j_{1} + 1,\chi } \right)}}{{\alpha^{{j_{1} + 1}} }} - \Gamma \left( {j_{2} + 1} \right) \hfill \\ \times \chi^{{j_{1} + 1}} \sum\limits_{n = 0}^{{\left\lceil {j_{2} } \right\rceil }} {\frac{1}{n!}} \left( {\frac{{\beta R_{2}^{\varepsilon } }}{\chi }} \right)^{n} G_{1,1;1,0;0,1}^{1,0;0,1;1,0} \left( {\left. {\begin{array}{*{20}c} {n - j_{1} } \\ {n - j_{1} + 1} \\ \end{array} } \right|\left. \begin{gathered} 1 \hfill \\ - \hfill \\ \end{gathered} \right|\left. \begin{gathered} - \hfill \\ 0 \hfill \\ \end{gathered} \right|\frac{1}{\chi \alpha },\frac{{\beta R_{2}^{\varepsilon } }}{\chi }} \right) \hfill \\ \end{gathered}$$

(60)

where,$G_{.,.;.,.;.,.}^{.,.;.,.;.,.} \left( {\left. . \right|\left. . \right|\left. . \right|.,.} \right)$ represents extended generalized bivariate Meijer G-function (EGBMGF) [32].

Now using (57) and (60),

$$I_{1} = \frac{{R_{2}^{\rho_l + 1} }}{\varepsilon w}\left( {f\left( {j_{1} ,\left\lceil {j_{2} + 1} \right\rceil } \right) - \left( {\beta R_{2}^{\varepsilon } } \right)^{ - w} f\left( {j_{1} + w,\left\lceil {j_{2} + w + 1} \right\rceil } \right)} \right)$$

(61)

where, $\left\lceil x \right\rceil$ is used to represent nearest integer greater than or equal to $x$.

Appendix 2: closed form for integral $I_{4}$

A generalised form for integral $I_{4}$ in (34) is given by (62)

$$I_{4} = \int\limits_{0}^{{R_{2} }} {r_{2}^{\rho_l } \int\limits_{0}^{\infty } {z^{{j_{2} }} e^{\alpha z} } } \Upsilon \left( {j_{1} + 1,\left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)} \right)dzdr_{2}$$

(62)

Use [30, 8.352.6] to expand incomplete gamma function

$$\Upsilon \left( {j_{1} + 1,\left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)} \right) = \Gamma \left( {j_{1} + 1} \right)\left( {1 - {\text{e}}^{{ - \left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)}} \sum\limits_{n = 0}^{{j_{1} }} {\frac{1}{n!}\left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)^{n} } } \right)$$

(63)

Now using binomial expansion and re-arranging (63) we get,

$$\Upsilon \left( {j_{1} + 1,\left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)} \right) = \Gamma \left( {j_{1} + 1} \right)\left( {1 - {\text{e}}^{{ - \left( {\beta + \chi \frac{{r_{2}^{\varepsilon } }}{z}} \right)}} \sum\limits_{n = 0}^{{j_{1} }} {\sum\limits_{m = 0}^{n} {\left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right)} \frac{{\beta^{n - m} \chi^{n} }}{n!}\left( {\frac{{r_{2}^{\varepsilon } }}{z}} \right)^{n} } } \right)$$

(64)

From (62) and (64),

$$\begin{aligned} I_{4} & = \Gamma \left( {j_{1} + 1} \right)\underbrace {{\int\limits_{0}^{{R_{2} }} {r_{2}^{\rho_l } \int\limits_{0}^{\infty } {z^{{j_{2} }} \,e^{ - \alpha z} } } dzdr_{2} }}_{{I_{5} }} \\ & \quad - {\text{e}}^{ - \beta } \Gamma \left( {j_{1} + 1} \right)\sum\limits_{n = 0}^{{j_{1} }} {\sum\limits_{m = 0}^{n} {\left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right)} \frac{{\beta^{n - m} \chi^{n} }}{n!}} \underbrace {{\int\limits_{0}^{{R_{2} }} {r_{2}^{\rho_l + \varepsilon n} \int\limits_{0}^{\infty } {z^{{j_{2} - n}} } } {\text{e}}^{{ - \left( {\alpha z + \frac{{\chi r_{2}^{\varepsilon } }}{z}} \right)}} dzdr_{2} }}_{{I_{6} }} \\ \end{aligned}$$

(65)

Integral $I_{5}$ in (65) can be solved using [30, 3.351.3], while $I_{6}$ can be represented as a modified Bessel function of second kind using [30, 3.471.9], and correspondingly in terms of Meijer –G function using [30, 9.34.3], we get

$$\begin{aligned} I_{4} & = \Gamma \left( {j_{1} + 1} \right)\frac{{R_{2}^{\rho_l + 1} }}{\rho_l + 1}\frac{{\Gamma \left( {j_{2} + 1} \right)}}{{\alpha^{{j_{2} + 1}} }} \\ & \quad - {\text{e}}^{ - \beta } \Gamma \left( {j_{1} + 1} \right)\sum\limits_{n = 0}^{{j_{1} }} {\sum\limits_{m = 0}^{n} {\left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right)} \frac{{\beta^{n - m} \chi^{n} }}{{n!\alpha^{\omega } }}} \int\limits_{0}^{{R_{2} }} {r_{2}^{\rho_l + \varepsilon n} } G_{0,2}^{2,0} \left( {\chi r_{2}^{\varepsilon } \alpha \left| \begin{gathered} - , - \hfill \\ 0,\omega \hfill \\ \end{gathered} \right.} \right)dr_{2} \\ \end{aligned}$$

(66)

where, $\omega$ is the nearest fraction to integer $\left( {j_{2} - n + 1} \right)$. Now utilizing [33], a closed form expression for integral $I_{4}$ is obtained in (67).

$$\begin{gathered} I_{4} = \Gamma \left( {j_{1} + 1} \right)\frac{{R_{2}^{\rho_l + 1} }}{\rho_l + 1}\frac{{\Gamma \left( {j_{2} + 1} \right)}}{{\alpha^{{j_{2} + 1}} }} \hfill \\ \begin{array}{*{20}c} {} & { - {\text{e}}^{ - \beta } \Gamma \left( {j_{1} + 1} \right)\sum\limits_{n = 0}^{{j_{1} }} {\sum\limits_{m = 0}^{n} {\left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right)} \frac{{\beta^{n - m} \chi^{{n - c_{l} }} }}{{n!\,\varepsilon \,\alpha^{{\omega + c_{l} }} }}} G_{1,3}^{2,1} \left( {\alpha \chi R_{2}^{\varepsilon } \left| \begin{gathered} 1 \hfill \\ c_{l} ,c_{l} + \omega ,0 \hfill \\ \end{gathered} \right.} \right)} \\ \end{array} \hfill \\ \end{gathered}$$

(67)

where, $c_{l} = {{\left( {\rho_{l} + m\varepsilon + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\rho_{l} + m\varepsilon + 1} \right)} \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }$.

Appendix 3: proof for (51)

From (48) and (49) the asymptotic form for integral $P_{2} \left( {C_{th} } \right)$ in (27) is given by (69)

$$P_{2}^{\infty } \left( {C_{th} } \right) \approx \sum\limits_{j = 0}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} }}{{R_{2}^{{\rho_{l} + 1}} }}} \frac{{d_{j0} \,d_{j} }}{{\Gamma \left( {j + 1} \right)}}\frac{1}{{2\sigma_{1}^{2} }}} \int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} }} \int\limits_{{a_{1} v}}^{\infty } {\Upsilon \left( {j + 1,\left( {\frac{{a_{2} vr_{2}^{\varepsilon } }}{{2\sigma_{2}^{2} z}}} \right)} \right)} dzdr_{2} }$$

(68)

Now using transformation,$x = 1/z$ and representing incomplete gamma function in form of confluent function using [34, 6.5.12] we get,

$$\begin{gathered} P_{2}^{\infty } \approx \sum\limits_{j = 0}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} }}{{R_{2}^{{\rho_{l} + 1}} }}} \frac{{d_{j0} d_{j} }}{{\Gamma \left( {j + 2} \right)}}\frac{{\left( {a_{2} v} \right)^{j + 1} }}{{2\sigma_{1}^{2} \left( {2\sigma_{2}^{2} } \right)^{j + 1} }}} \hfill \\ \begin{array}{*{20}c} {} & { \times \int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} + \varepsilon \left( {j + 1} \right)}} \int\limits_{0}^{{1/a_{1} v}} {x^{j - 1} e^{{ - \frac{{a_{2} vr_{2}^{\varepsilon } }}{{2\sigma_{2}^{2} }}x}} {}_{1}F_{1} \left( {1,j + 2,\frac{{a_{2} vr_{2}^{\varepsilon } }}{{2\sigma_{2}^{2} }}x} \right)} \,dxdr_{2} } } \\ \end{array} \hfill \\ \end{gathered}$$

(69)

Lower order integral in (69) can be solved by using [35]

$$\begin{aligned} P_{2}^{\infty } \left( {C_{th} } \right) & \approx \sum\limits_{j = 0}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} }}{{R_{2}^{{\rho_{l} + 1}} }}} \frac{{d_{j0} d_{j} }}{{j\,\Gamma \left( {j + 2} \right)\,}}\frac{1}{{\,2\sigma_{1}^{2} (a_{1} v)^{j} }}\left( {\frac{{a_{2} v}}{{2\sigma_{2}^{2} }}} \right)^{j + 1} } \\ & \quad \times \int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} + \varepsilon (j + 1)}} {}_{1}F_{1} \left( {j,j + 2, - \frac{{a_{2} }}{{a_{1} 2\sigma_{2}^{2} }}r_{2}^{\varepsilon } } \right)dr_{2} } \\ \end{aligned}$$

(70)

Integral in (70) can be solved using transformation $r_{2}^{\varepsilon } = z$ and [34] using property ${}_{1}F_{1} \left( {j,j + 2, - cz} \right) = e^{ - cz} {}_{1}F_{1} \left( {2,j + 2,cz} \right)$,

$$\begin{gathered} P_{2}^{\infty } \left( {C_{th} } \right) \approx \sum\limits_{{j = 0^{ + } }}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} \,d_{j0} d_{j} }}{{j\,\Gamma \left( {j + 2} \right)\,}}} \frac{1}{{\,2\sigma_{1}^{2} (a_{1} v)^{j} }}\left( {\frac{{a_{2} v}}{{2\sigma_{2}^{2} }}} \right)^{j + 1} } \hfill \\ \begin{array}{*{20}c} {} & { \times \frac{{r_{2}^{{\varepsilon \left( {j + 1} \right)}} }}{{\left( {\rho_{l} + \varepsilon \left( {j + 1} \right) + 1} \right)}}{}_{2}F_{2} \left( {j,\alpha ,j + 2,\alpha + 1, - \frac{{a_{2} }}{{a_{1} 2\sigma_{2}^{2} }}r_{2}^{\varepsilon } } \right)} \\ \end{array} \hfill \\ \end{gathered}$$

(71)

where, $\alpha = \frac{{\rho_{l} + \varepsilon \left( {j + 1} \right) + 1}}{\varepsilon }$.

Appendix 4: proof for (53)

From (34) and (49) asymptotic expression for $EOP_{AP}^{\infty }$ is given by (73)

$$\begin{gathered} EOP_{AF}^{\infty } \approx \sum\limits_{j = 0}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} }}{{R_{2}^{{\rho_{l} + 1}} }}} \frac{{d_{j0} d_{j} }}{{\Gamma \left( {j + 1} \right)}}} \frac{1}{{2\sigma_{1}^{2} \left( {2\sigma_{2}^{2} } \right)^{j + 1} }} \hfill \\ \begin{array}{*{20}c} {} & {} & { \times \int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} }} \int\limits_{0}^{\infty } {z^{j} e^{{ - z/2\sigma_{2}^{2} }} \left( {\frac{{vb_{3} }}{{b_{1} }} + \frac{{b_{2} vr_{2}^{\varepsilon } }}{{b_{1} z}}} \right)} dzdr_{2} } } \\ \end{array} \hfill \\ \end{gathered}$$

(72)

or

$$\begin{gathered} EOP_{AF}^{\infty } \approx \sum\limits_{j = 0}^{{N_{T} }} {\sum\limits_{l = 1}^{L} {\frac{{\vartheta_{l} }}{{R_{2}^{{\rho_{l} + 1}} }}} \frac{{d_{j0} \,d_{j} }}{{\Gamma \left( {j + 1} \right)}}} \frac{1}{{\,2\sigma_{1}^{2} \left( {2\sigma_{2}^{2} } \right)^{j + 1} }} \hfill \\ \begin{array}{*{20}c} {} & { \times \left( {\frac{{vb_{3} }}{{b_{1} }}\int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} }} \int\limits_{0}^{\infty } {z^{j} \,e^{{ - z/2\sigma_{2}^{2} }} } dzdr_{2} } + \frac{{vb_{2} }}{{b_{1} }}\int\limits_{0}^{{R_{2} }} {r_{2}^{{\rho_{l} + \varepsilon }} \int\limits_{0}^{\infty } {z^{j - 1} \,e^{{ - z/2\sigma_{2}^{2} }} } dzdr_{2} } } \right)} \\ \end{array} \hfill \\ \end{gathered}$$

(73)

Now using [30, 3.351.3] and solving integral in (73), asymptotic expression for EOP is obtained in (53).