Abstract
This paper explores some issues about the choice of variables for causal representation and explanation. Depending on which variables a researcher employs, many causal inference procedures and many treatments of causation will reach different conclusions about which causal relationships are present in some system of interest. The assumption of this paper is that some choices of variables are superior to other choices for the purpose of causal analysis. A number of possible criteria for variable choice are described and defended within a broadly interventionist approach to causation.
Similar content being viewed by others
Notes
Discussions of “cognitive ontology” among cognitive neuroscientists such as Lenartowicz et al. (2010) are in effect debates about how to choose “cognitive” variables on the basis of neural information, with the suspicion being frequently voiced that our current stock of variables is unprincipled and often an obstacle to casual understanding.
Thanks to Clark Glymour for this observation.
Other examples: Should we think in terms of just one intelligence variable (g—for general intelligence) or many different forms of intelligence? Different choices will likely lead to different conclusions about the causal influences at work. Is it reasonable to conceptualize “risk-taking” as general tendency (i.e., a single variable) and then investigate its genetic etiology?
To forestall an obvious criticism this is not the claim that variables should be chosen so that all possible interventionist dependency relations can be captured. My claim is merely that it is sometimes a defect in variable choice if it does not allow some such relations to be captured.
For those worried that this characterization is overly restrictive, several additional considerations may be helpful. First, a number of the features of good variables on which I focus are also justifiable in terms of other frameworks for thinking about causal explanation. For example, stability or generalizability is a desideratum on many theories of causal explanation. Finding counterfactual supporting dependency relations is also a goal of many theories that do not think of those dependency relations in specifically interventionist terms. Second, even if successful causal explanation involves more than just the features on which the interventionist conception focuses, as long as that conception captures some relevant features of causal explanation, it may be a useful source of constraints on variable choice.
For support for the empirical claim that common sense casual inquiry is guided by a preference for sparse causal representations in the sense described in Sect. 11, see Liu et al. (2008).
Another clarification: an anonymous referee worries that talk of goals of inquiry makes the “the truth of causal claims depend on the circumstances and goals of an inquiry rather than merely the system in question” and “leads to an “interest-relative” notion of causation. This is a misunderstanding. First, as should be clear from my discussion above, by goals of inquiry, I have in mind broad cognitive aims like provision of causal explanations as opposed to, say, “prediction”, rather than the idiosyncratic preferences of particular investigators for certain variables (such as the preferences of some psychologists for only behavioral variables). Second, once these broad goals are sufficiently specified, I take it to be an “objective” matter, not dependent on further facts about anyone’s interests, whether certain choices conduce to the goals—it is the nature of the system under investigation that determines this. Thus, if the specified goal is to find variables that maximize predictive accuracy according to some criterion, it is empirical features of the system investigated which determine which variables will do this. Similarly, if one’s goal is causal explanation. If investigator X is not interested in causal explanation but instead just in prediction and chooses variables accordingly and investigator Y is interested in causal explanation and chooses variables accordingly, we should not think of this as a case in which the truth of causal claims made by X and Y somehow varies depending on X and Y’s interests or the variables they choose. Instead X is not in the business of making causal claims and if the predictive claims X makes are interpreted causally (e.g. as predictions of the outcomes of interventions) presumably many of them will be false. Thus once one decides to adopt the goal of casual explanation and fleshes this out in a specific way, one is locked into certain criteria for what constitutes success in this enterprise—or so I assume. I will add that the idea that there is a conflict between, on the one hand, representing causal relations “as they really are” and, on the other hand, thinking in terms of goals of inquiry is misconceived: representing causal relations as they are (and so on) just is one possible goal of inquiry.
Finally, in connection with “goals” let me acknowledge the role of an additional (obvious) consideration : even given the broad goal of causal analysis, different researchers may target different systems or different features of systems for analysis: researcher A may be interested in a causal analysis of the molecular process involved in the opening an closing of individual ion channels during the generation of the action potential, while researcher B is interested in causal understanding of the overall circuit structure of the neuron that allows it to generate an action potential rather than some other response. Again, I take this sort of interest-relativity to be no threat to the “objectivity” of the resulting causal claims.
This contrast between relational and non-relational criteria is due to David Danks.
See Hitchcock (2012) for an application of this general strategy in connection with issues concerning the metaphysics of events.
For example, one might take R to be a difference-making or dependency relationship of some kind appropriate to characterizing causation—R might be understood in terms of counterfactual dependence, statistical dependence or along interventionist lines. For each of these understandings of R, one can ask questions parallel to those described above about how the R-relation between variables behaves under various transformations of those variables.
See Bass (2014, p. 8) for discussion. Basically this follows because the sigma-field generated by F(X) is a subfield of the sigma field generated by X and similarly for Y and G(Y). Hand-wavey proof in order to avoid measure-theoretic complications: Knowing the values of X conveys information about the values of F(X) but the latter can only be a subset of the information carried by the values of X. Similarly the information carried by the values of G(Y) can be thought of as a subset of the information carried by the values of Y. Thus if
 , then F(X) should not tell us anything about G(Y). If it did—if
, then F(X) should not tell us anything about G(Y). If it did—if  —this could only happen because values of X contain information about values of Y.
—this could only happen because values of X contain information about values of Y.Proof: Assume for purposes of contradiction that F, G are bijective and (i)
 but (ii)
but (ii)  . Then \(F^{-1}, G^{-1}\) are also functions, and hence from (ii) and (6.2),
. Then \(F^{-1}, G^{-1}\) are also functions, and hence from (ii) and (6.2),  , which contradicts (i).
, which contradicts (i).A further thought is that the more interesting practical question is which transformations take relationships of dependency into relationships of “almost” independence—i.e., relationships that are sufficiently close to independence as to be indistinguishable from it for various purposes.
A similar suggestion that independencies can be valuable is made in Danks (2014).
See Spirtes (2009) for a similar observation. I am much indebted to this extremely interesting paper.
Danks (personal communication) suggests that this notion of “independent manipulability” might be operationalized, in the case of structural equations and directed graph representations, in terms of the assumption of “independent noise distributions. ” That is, in cases in which each variable is influenced by an additive noise or error term, we might choose variables so that the distributions of the noise term are (approximately) independent of one another and perhaps also so that errors are independent of the other independent variables in the equations in which the errors occur. This corresponds to the idea that Nature can independently “manipulate” each variable. This idea is exploited in machine learning algorithms for causal inference.
Indeed, I make use of a version of it in Author, forthcoming.
Many philosophers, especially those with a metaphysical bent, may be inclined to resist the suggestion that considerations having to do with what we can actually manipulate should influence choice of variables for causal representation on the grounds that this makes variable choice excessively “pragmatic” or even “anthropocentric”. But (i) like it or not, “actually existing science” does exhibit this feature, and (ii) it is methodologically reasonable that it does—why not adopt variables which are such that you can learn about causal relationships by actually manipulating and measuring them and, other things being equal, avoid using variables for which this not true? Moreover, (iii) at least in many cases, there are “objective” considerations rooted in the physical nature of the systems under investigation that explain why some variables that can be used to describe those systems are manipulable and measurable by macroscopic agents like us and other are not. For example, any such manipulable/ measurable variable will presumably need to be temporally stable over macroscopic scales at which we operate. The physics of gases explains why, e.g., pressure has the feature and other variables we might attempt to define do not—again, see Callen (1985), who emphasizes the importance of considerations having to do with actual manipulability in characterizing fundamental thermodynamic variables. The contrast between “heat” and “work” represents another interesting illustration, since this is essentially the contrast between energy that can be manipulated by a macroscopic process and energy that is not so controllable. Presumably one does not want to conclude that this contrast is misguided.
Very roughly this is because in cases of this sort, all these accounts employ (for this case) some variant on the following test for whether X taking some value x is an actual cause of Y taking value y: draw a directed graph of the causal structure, and then examine each directed path from X to Y. If, for any such path, fixing variables along any other path from X to Y at their actual values, the value of Y depends on the value of X, then X is an actual cause of Y. If RH and LH are employed as variables, then fixing LH at its actual value \(({LH=0})\), the arrival (A) of the train depends on the value of RH. On the other hand, if a single variable S is employed, there is only a single path from S to A. In this case the value of A does not depend on the value of S since the train will arrive for either value of S.
Similar points hold for the representation of type-level causal relationships. Given a structure (i) in which distinct variables X and Y are represented as joint effects of a common cause C, we might instead (ii) collapse X and Y into a single variable Z represented as the single effect of C. (i) and (ii) involve different, non-equivalent assumptions about causal relationships. Criteria like those described above can be used to guide which choice is appropriate.
To use Spirtes’ example, the variables might be ordered as \(<\)A,B,C\(>\), where each temporally indexed A variable is directly caused only by other A variables (which are not later in the ordering \(<\)A,B,C\(>\)), each temporally indexed B variable is directly caused only by A variables (which are not later in the ordering \(<\)A,B,C\(>\)), and each temporally indexed C variable is directly caused only by B variables (which are not later in the ordering \(<\)A,B,C\(>\)). The time-index free graph thus allows one to collapse the temporal structure in the original graph consistently with the causal ordering.
Moreover, for any graph with a substantial number of variables, there will be a large equivalence class of such fully connected graphs that capture the (in)dependence relations. Absent some other source of information, one will not know which if any of these graphs is correct—a point to which I will return in Sect. 10.
Of course there are other constraints as well that might be combined with CMC—one of the best known and most powerful is faithfulness in the sense of Spirtes et al. (2000). Reasons of space prevent consideration of this constraint interacts with variable choice.
In addition when purported causal relationships are relatively unstable, holding only in a narrow range of circumstances, grounds for worry about “overfitting” become more pronounced.
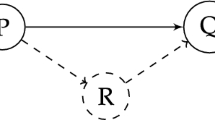
At the risk of belaboring the obvious, let me emphasize that this is not a matter of the \(G \rightarrow R\) relationship being more likely to be true; it is rather that this relationship provides information about something that we want to know about.
Note that this is a matter of the relation between, on the one hand TC and D, and on the other hand, LDC, HDC and D, thus again illustrating the theme that relations among variables matter for variable choice.
For evidence regarding lay subjects in support of this claim, see Lu et al. (2008). The authors model causal learning within a Bayesian framework which assumes subjects have generic priors that favor the learning of what the authors call “sparse and strong” causal relationships over alternatives. Strength in this context means that causes have high “causal power” in the sense of Cheng (1997)—“power” is a stability-related notion. Sparseness means, roughly, that relatively few causal relationships are postulated—this is obviously related to specificity. Lu et al. present evidence that, as a descriptive matter, subject’s learning conforms to what would be expected if they were guided by such priors and they also gesture at a normative rationale for their use—they facilitate learning and have an information-theoretic justification in the sense that strong and sparse causes are more informative about their effects.
References
Bass, R. (2014). Probability theory. http://homepages.uconn.edu/~rib02005/gradprob.pdf. Accessed 15 March 2015.
Callen, H. (1985). Thermodynamics and an introduction to thermostatics. New York: Wiley.
Cheng, P. (1997). From covariation to causation: A causal power theory. Psychological Review, 104, 367–405.
Danks, D. (2014). Goal-dependence in (scientific) ontology. Synthese. doi:10.1007/s11229-014-0649-1
Glymour, C. (2007). When is a brain like a planet? Philosophy of Science, 74, 330–347.
Glymour, C., & Glymour, M. (2014). Race and sex are causes. Epidemiology, 25(4), 488–490.
Halpern, J., & Hitchcock, C. (2010). Actual causation and the art of modeling. In R. Dechter, H. Geffner, & J. Halpern (Eds.), Heuristics, probability and causality: a tribute to judea pearl. London: College Publications.
Halpern, J., & Pearl, J. (2005). Causes and explanations: A structural-model approach. Part 1: Causes. British Journal for the Philosophy of Science, 56, 843–887.
Hernan, M., & Taubman, S. (2008). Does obesity shorten life? The importance of well-defined interventions to answer causal questions. International Journal of Obesity, 32, S8–14.
Hitchcock, C. (2001). The intransitivity of causation revealed in equations and graphs. Journal of Philosophy, 98, 273–299.
Hitchcock, C. (2012). Events and times: A case study in means-ends metaphysics. Philosophical Studies, 160, 79–96.
Kendler, K. (2005). A gene for\({\ldots }\): The nature of gene action in psychiatric disorders. American Journal of Psychiatry, 162, 1243–1252.
Lenartowicz, A., Kalar, D., Congdon, & Poldrack, R. (2010). Towards an ontology of cognitve control. Topics in Cognitive Science, 2, 678–692.
Lewis, D. (1973). Causation. The Journal of Philosophy, 70, 556–567.
Lewis, D. (1983). New work for a theory of universals. Australasian Journal of Philosophy, 61, 343–377.
Lu, H., Yuille, A., Liljeholm, M., Cheng, P., & Holyoak, K. (2008). Bayesian generic priors for causal learning. Psychological Review, 115, 955–984.
Paul, L., & Hall, N. (2013). Causation: A user’s guide. Oxford: Oxford University Press.
Salmon, W. (1984). Scientific explanation and the causal structure of the world. Princeton: Princeton University Press.
Sider, T. (2011). Writing the book of the world. Oxford: Oxford University Press.
Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, prediction, and search (2nd ed.). Cambridge: MIT Press.
Spirtes, P. (2009). Variable definition and causal inference. Proceedings of the 13th international congress of logic methodology and philosophy of science (pp. 514–553).
Spirtes, P., & Scheines, R. (2004). Causal inference of ambiguous manipulations. Philosophy of Science, 71, 833–845.
Strevens, M. (2007). Review of woodward, making things happen. Philosophy and Phenomenological Research, 74, 233–249.
Woodward, J. (2003). Making things happen: A theory of causal explanation. New York: Oxford University Press.
Woodward, J. (2006). Sensitive and insensitive causation. The Philosophical Review, 115, 1–50.
Woodward, J. (2010). Causation in biology: Stability, specificity, and the choice of levels of explanation. Biology and Philosophy, 25, 287–318.
Acknowledgments
It is a great pleasure to be able to contribute this essay to this special journal issue on the philosophy of Clark Glymour. There is no one in philosophy whose work I admire more. I have benefited from a number of conversations with Clark on the topic of this essay. I’ve also been greatly helped by discussions with David Danks, Frederick Eberhardt, Chris Hitchcock and Peter Spirtes, among others. A version of this paper was given at a workshop on Methodology and Ontology at Virginia Tech in May, 2013 and I am grateful to audience members for their comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Woodward, J. The problem of variable choice. Synthese 193, 1047–1072 (2016). https://doi.org/10.1007/s11229-015-0810-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0810-5




 , then F(X) should not tell us anything about G(Y). If it did—if
, then F(X) should not tell us anything about G(Y). If it did—if  —this could only happen because values of X contain information about values of Y.
—this could only happen because values of X contain information about values of Y. but (ii)
but (ii)  . Then
. Then  , which contradicts (i).
, which contradicts (i).