Abstract
This paper expounds that besides the well-known spatio-temporal problem there is a causal problem of entanglement: even when one neglects spatio-temporal constraints, the peculiar statistics of EPR/B experiment is inconsistent with usual principles of causal explanation as stated by the theory of causal Bayes nets. The conflict amounts to a dilemma that either there are uncaused correlations (violating the causal Markov condition) or there are caused independences (violating the causal faithfulness condition). I argue that the central ideas of causal explanations can be saved if one accepts the latter horn and explains the unfaithful independences by a stable fine-tuning of the causal parameters.










Similar content being viewed by others
Notes
The measurement settings have often been called ‘parameters’ in the discussion about Bell’s theorem. Since the latter term is rather unspecific and might lead to confusions with the parameters of causal models (see fn.15), I shall not use it for the measurement settings of EPR/B experiments.
We shall use the convention to denote variables in bold fonts, e.g. \(\varvec{\alpha }\), and corresponding values of variables in normal font, e.g. \(\alpha \); specific values of variables are indicated by an index, e.g. \(\alpha _+\).
Assuming e.g. the maximally entangled state \(\psi = (|+\rangle |+\rangle + |-\rangle |-\rangle ) / \sqrt{2} \), the correlations are given by
$$\begin{aligned} P(\alpha \beta | a b \psi )&= {\left\{ \begin{array}{ll} \frac{1}{2}\cos ^2 (a-b) &{} \text {if } \alpha = \beta \\ \frac{1}{2} \sin ^2 (a-b) &{} \text {if } \alpha \ne \beta . \end{array}\right. } \end{aligned}$$(1)I have not evaluated actual measurement data but have calculated these statistical facts from the theoretical probability distribution (1) of quantum mechanics, which is well-known to correctly describe the empirical findings.
Note that this is not the usual form of the Markov condition (which rather says that a variable in a causal graph is statistically independent of all its non-effects given its direct causes; Spirtes et al. 1993, sect. 3.4.1), but the formulations are equivalent and the present formulation (which is sometimes called‘d-separation criterion’, cf. Pearl 1988, sect. 3.3.1, and also Pearl 2000, pp. 16ff, as well as Spirtes et al. 1993, sect. 3.7.1) is the most general and the most appropriate one for elucidating the project of causal explanation.
As for the Markov condition this is not the usual form of the faithfulness condition, but the most general and most appropriate one. It has been suggested by Schurz and Gebharter (2015), and it has the advantage to provide a formulation of the faithfulness condition that is logically independent of the Markov condition.
A typical maximally entangled state such as \(\psi = (|+\rangle |+\rangle + |-\rangle |-\rangle ) / \sqrt{2}\) is a special case of a more general state \(\psi ^\prime = \sqrt{p} \; |+\rangle |+\rangle + \sqrt{1-p} \; |-\rangle |-\rangle \), viz. for \(p=1/2\). For \(p=1/2 \pm \epsilon \) with \(\epsilon >0\) small, the state is only partially entangled but close enough to maximal entanglement in order to still violate the Bell inequalities.
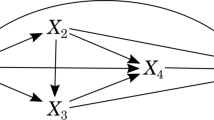
Given only the five observable variables of the setup, it is easy to show that the connections must be direct. Since due to the intervention assumption the settings and the quantum state are exogenous, the only way for \(\varvec{a} \rightarrow \ldots \rightarrow \varvec{\alpha }\) to be realised indirectly would be via the other outcome, i.e. \(\varvec{a} \rightarrow \varvec{\beta }\rightarrow \varvec{\alpha }\); but by the faithfulness condition this route would violate the empirical independence \(\text {I}(\varvec{\beta }, \varvec{a})\). (An analogous argument holds for the case that the connection \(\varvec{b} \rightarrow \ldots \rightarrow \varvec{\alpha }\) must be direct.) Similarly, a connection \(\varvec{\psi }\rightarrow \ldots \rightarrow \varvec{\alpha }\) can only be indirect via the other outcome, i.e. \(\varvec{\psi }\rightarrow \varvec{\beta }\rightarrow \varvec{\alpha }\); but if this is the only connection between \(\varvec{\psi }\) and \(\varvec{\alpha }\), i.e. if there is no direct connection between them, the Markov condition would imply \(\text {I}(\varvec{\alpha }, \varvec{\psi }| \varvec{\beta })\), which contradicts the empirical dependence \(\lnot \text {I}(\varvec{\alpha }, \varvec{\psi }| \varvec{\beta })\) (and analogously for the connection \(\varvec{\psi }\rightarrow \ldots \rightarrow \varvec{\beta }\)).
A variable \(\varvec{X}\) is a common cause of two other variables \(\varvec{Y}\) and \(\varvec{Z}\) iff (i) there is a directed causal path from \(\varvec{X}\) to \(\varvec{Y}\) and (ii) there is a directed causal path from \(\varvec{X}\) to \(\varvec{Z}\). A common cause \(\varvec{X}\) is a true common cause iff it further fulfils the condition that (iii) no other variable besides \(\varvec{X}\) is on both of these paths.
Specifically the independences needed for Bell’s theorem are local factorisation, \(P(\alpha \beta | a b \psi \lambda ) = P(\alpha | a \psi \lambda )\cdot P(\beta | b \psi \lambda )\), and autonomy, \(P(\lambda | a b \psi ) = P(\lambda | \psi )\).
It has been noticed that there might be ways for local structures to explain the EPR/B correlations (in accordance with all principles mentioned so far), if one assumes that the measured photon pairs are not a representative sample of the population of all values of \(\varvec{\lambda }\) (selection bias, ‘detection loophole’; Pearle 1970; Clauser and Horne 1974; Fine 1982; Maudlin 1994, ch. 6). This scenario rests on the fact that actual photon detectors are inefficient and do not measure all emitted pairs of photons. However, very precise measurements with entangled ions can detect every member of an ensemble of entangled objects (Rowe et al. 2001) and yield the same kind of strong correlations, confirming empirically that EPR/B correlations cannot be explained locally by selection bias (Grangier 2001).
More precisely, my argument shows that acyclicity, the causal Markov condition, the causal faithfulness condition, the intervention assumption, the causal sufficiency assumption (for the set of six variables assumed in Fig. 3) and the measurement statistics form an inconsistent set. The measurement statistics is an empirical fact, so it must be true. Furthermore, one can show mathematically that violating causal sufficiency by assuming further latent common causes does not suffice to explain the strong EPR/B correlations (Näger 2013a). Hence, one of the former four assumptions must give. Here I concentrate my discussion on the dilemma between giving up the Markov or the faithfulness condition. To be clear, there might also be solutions involving a failure of acyclicity or the intervention assumption. Concerning the latter there are models that are well-known to be able to explain the statistics of EPR/B experiments by assuming influences from the latent common cause \(\varvec{\lambda }\) to each setting (Suppes and Zanotti 1981). Since the settings are externally controlled such proposals require that \(\varvec{\lambda }\) influences whatever determines the setting, e.g. the experimenter or a random number generator etc. Such undifferentiated influences, which violate condition (ii) of the intervention assumption, have been criticised to introduce a ‘cosmic conspiracy’ in nature and to be completely ad hoc. For the other, there are also models asserting to explain the EPR/B correlations by a local causal structure and causal cycles between the emitting source and the absorbing detectors (Cramer 1986). However, the model is committed to a rather unusual causal story (the cyclical interactions from one space-time point to another and back are said to happen in “pseudotime”), and it has been objected that the resulting loops yield inconsistencies (Maudlin 1994, ch. 7).
Note that in our overview of prototypes we have drawn asymmetric structures which only involve unfaithful independences of group 1, but we could as well have depicted the corresponding mirror images which only involve unfaithful independences of group 2, e.g. involving \(\varvec{a} \rightarrow \varvec{\lambda }\) instead of \(\varvec{b} \rightarrow \varvec{\lambda }\) in Fig. 3d. It is clear that there are also symmetric structures which make the independences in both groups unfaithful (e.g. involving \(\varvec{a} \rightarrow \varvec{\lambda }\) additional to \(\varvec{b} \rightarrow \varvec{\lambda }\) in Fig. 3d); we have not depicted them because involving two groups of unfaithfulness would make the subsequent discussion of how to deal with the unfaithfulness unnecessarily complicated; but at the end of our investigation we will be able to easily generalise our results to symmetric structures.
Following Schurz and Gebharter (2015), I understand causal parameters (i.e. the parameters of a given causal model) as the conditional probabilities of each variable conditional on its direct causes, \(P(\varvec{x} | \text {DC}(\varvec{x}))\), which is the most general definition of such parameters, allowing also for purely indeterministic models. A definition restricted to deterministic models has been given by (Pearl 2000, p. 44): according to such models, the value of each variable is determined by a function \(\varvec{x} = f(\text {DC}(\varvec{x}))+ \varvec{u_x}\) and the parameters are those functions plus a probability distribution over the independent error variables \(\varvec{u_x}\).
Note, however, that in the modified theory causal discovery becomes much more complicated: while in the original theory a statistical independence implies a causal independence (by faithfulness), by constrained faithfulness it either requires a causal independence or a causal dependence with fine-tuning. For this reason, the causal discovery algorithms of the original theory, which essentially require the faithfulness condition, do not work any more, if one just assumes the weaker principle constrained faithfulness.
Whether there are also additional unconditional independences due to determinism is an open question, because SGS’s method to calculate the extra independences is not proven to yield a complete set of additional independences. Presently, there is, however, no hint that there are.
‘Threshold’ is my name. I prefer it over ‘non-transitivity’ because it will turn out that there is another kind of a non-transitive unfaithfulness (see unfaithfulness by internal cancelling paths below).
‘Masking’ is again my terminology. (Pearl 1988, p. 93) has introduced this kind of unfaithfulness with an example of a bell that rings, when the outcomes of tossing two independent fair coins agree, but he has not given it a name. Pearl’s example is very specific (highly symmetric) and here I present a more general (asymmetric) version.
For lack of space I cannot present the details of the quantum mechanical explanation here; they will be expounded elsewhere.
References
Aspect, A., Dalibard, J., & Roger, G. (1982). Experimental test of Bell’s inequalities using time-varying analyzers. Physical Review Letters, 49, 1804–1807.
Bell, J. S. (1964). On the Einstein-Podolsky-Rosen paradox. Physics, 1(3), 195–200.
Bell, J. S. (1975). The theory of local beables. TH-2053-CERN (Reprinted in Bell 1987).
Bell, J. S. (1987). Speakable and unspeakable in quantum mechanics: Collected papers on quantum mechanics. Cambridge: Cambridge University Press.
Bohm, D. (1951). Quantum theory. Englewood Cliffs, NJ: Prentice-Hall.
Butterfield, J. (1989). A space-time approach to the Bell inequality. In J. T. Cushing & E. McMullin (Eds.), Philosophical consequences of quantum theory: Reflections on Bell’s theorem (pp. 114–144). Notre Dame: University of Notre Dame Press.
Cartwright, N. (1988). How to tell a common cause. In J. H. Fetzer (Ed.), Probability and causality: Essays in honor of Wesley C. Salmon (pp. 181–188). Dordrecht: Reidel.
Cartwright, N. (2007). Hunting causes and using them: Approaches in philosophy and economics. Cambridge: Cambridge University Press.
Clauser, J. F., & Horne, M. A. (1974). Experimental consequences of objective local theories. Physical Review D, 10(2), 526–535.
Cramer, J. G. (1986). The transactional interpretation of quantum mechanics. Reviews of Modern Physics, 58, 647–687.
Einstein, A., Podolsky, B., & Rosen, N. (1935). Can quantum mechanical description of physical reality be considered complete? Physical Review, 47, 777–780.
Fine, A. (1982). Some local models for correlation experiments. Synthese, 50, 279–294.
Glymour, C. (2006). Markov properties and quantum experiments. In W. Demopoulos & I. Pitowsky (Eds.), Physical theory and its interpretation: Essays in honor of Jeffrey Bub (pp. 117–125). Dordrecht: Springer.
Grangier, P. (2001). Quantum physics: Count them all. Nature, 409, 774–775.
Jarrett, J. P. (1989). Bell’s theorem: A guide to the implications. In J. T. Cushing & E. McMullin (Eds.), Philosophical consequences of quantum theory: Reflections on Bell’s theorem (pp. 60–79). Notre Dame: University of Notre Dame Press.
Maudlin, T. (1994). Quantum non-locality and relativity: Metaphysical intimations of modern physics. Oxford: Blackwell. (3rd ed. Wiley-Blackwell 2011).
Näger, P. M. (2013a). Causal graphs for EPR experiments. Preprint. http://philsci-archive.pitt.edu/9915/.
Näger, P. M. (2013b). A stronger Bell argument for quantum non-locality. Preprint. http://philsci-archive.pitt.edu/9932/.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems: Networks of plausible inference. San Mateo: Morgan Kaufmann.
Pearl, J. (2000). Causality: Models, reasoning, and inference. Cambridge: Cambridge University Press.
Pearle, P. M. (1970). Hidden-variable example based upon data rejection. Physical Review D, 2(8), 1418–1425.
Rowe, M. A., Kielpinski, D., Meyer, V., Sackett, C. A., Itano, W. M., Monroe, C., et al. (2001). Experimental violation of a Bell’s inequality with efficient detection. Nature, 409, 791–794.
Schurz, G., & Gebharter, A. (2015). Causality as a theoretical concept: Explanatory warrant and empirical content of the theory of causal nets. Synthese. doi:10.1007/s11229-014-0630-z.
Shimony, A. (1984). Controllable and uncontrollable non-locality. In S. Kamefuchi (Ed.), Foundations of quantum mechanics in the light of new technology (pp. 225–230). Tokyo: The Physical Society of Japan.
Spirtes, P., Glymour, C., & Scheines, R. (1993). Causation, prediction, and search. New York: Springer. (2nd ed. MIT Press 2000).
Suppes, P., & Zanotti, M. (1981). When are probabilistic explanations possible? Synthese, 48, 191–199.
van Fraassen, B. C. (1982a). The charybdis of realism: Epistemological implications of Bell’s inequality. Synthese, 52, 25–38.
van Fraassen, B. C. (1982b). Rational belief and the common cause principle. In R. McLaughlin (Ed.), What? Where? When? Why? Essays on induction, space and time, explanation (pp. 193–209). Dordrecht: Reidel.
Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., & Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039–5043.
Wood, C. J. & R. W. Spekkens (2012). The lesson of causal discovery algorithms for quantum correlations: Causal explanations of Bell-inequality violations require fine-tuning. Preprint. http://arxiv.org/abs/1208.4119v1
Acknowledgments
I would like to thank Frederick Eberhardt, Alexander Gebharter, Clark Glymour, Kevin Kelly, Meinard Kuhlmann, Gerhard Schurz, Manfred Stöckler, Michael Zehetleitner and audiences at the Düsseldorf Center for Logic and Philosophy of Science, at the Munich Center for Mathematical Philosophy and at the Workshop ‘Physics and Causality’ (Deutsche Physikalische Gesellschaft, Munich, 2012) for helpful comments and discussion. Research for this paper was supported by the Deutsche Forschungsgemeinschaft (DFG).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Näger, P.M. The causal problem of entanglement. Synthese 193, 1127–1155 (2016). https://doi.org/10.1007/s11229-015-0668-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0668-6