Minimal Varieties of Involutive Residuated Lattices | Studia Logica Skip to main content
Springer Nature Link
Log in

Minimal Varieties of Involutive Residuated Lattices

  • Published:
Studia Logica Aims and scope Submit manuscript

Abstract

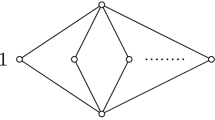
We establish the existence uncountably many atoms in the subvariety lattice of the variety of involutive residuated lattices. The proof utilizes a construction used in the proof of the corresponding result for residuated lattices and is based on the fact that every residuated lattice with greatest element can be associated in a canonical way with an involutive residuated lattice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. BARR, M., ‘^-Autonomous Categories’, Led. Notes in Math. 752, Springer, Berlin, 1979.

    Google Scholar 

  2. BLOK, W. J., and I. M. A. FERREIRIM, ‘On the structure of hoops’, Algebra Univer-salis 43 (2000), 233–257.

    Article  Google Scholar 

  3. BLOK, W. J., and J. G. RAFTERY, ‘Varieties of commutative residuated integral pomonoids and their residuation subreducts’, J. Algebra 190 (1997), 280–328.

    Article  Google Scholar 

  4. BLOUNT, K., and C. TSINAKIS, ‘The structure of residuated lattices’, Intemat. J. Algebra Comput. 13(4) (2003), 437–461.

    Article  Google Scholar 

  5. GALATOS, N., ‘Minimal varieties of residuated lattices’, Algebra Univers. 52(2) (2005), 215–239.

    Article  Google Scholar 

  6. GALATOS, N., and J. G. RAFTERY, ‘Adding involution to residuated structures’, Stu-dia Logica 77 (2004), 181–207.

    Article  Google Scholar 

  7. GALATOS, N., and C. TSINAKIS, ‘Generalized MV-algebras’, J. Algebra 283(1) (2005), 254–291.

    Article  Google Scholar 

  8. HART, J., L. RAFTER, and C. TSINAKIS, ‘The structure of commutative residuated lattices’, Internal. J. Algebra Comput. 12(4) (2002), 509–524.

    Article  Google Scholar 

  9. JlPSEN, P., and C. TSINAKIS, ‘A survey of residuated lattices’, Ordered Algebraic Structures (J. Martinez, ed.), Kluwer Academic Publishers, Dordrecht, 2002, 19–56.

    Google Scholar 

  10. JONSSON, B., ‘Algebras whose congruence lattices are distributive’, Math. Scand. 21 (1967), 110–121.

    Google Scholar 

  11. JONSSON, B., and C. TSINAKIS, ‘Products of classes of residuated structures’, Studio, Logica 77 (2004), 267–292.

    Article  Google Scholar 

  12. PAOLI, P., Substructural Logics: A Primer, Trends in Logic, Kluwer Academic Publishers, Dordrecht, 2002.

    Google Scholar 

  13. PAOLI, P., ‘^-autonomous lattices’, Studia Logica 79(2) (2005), 283–304.

    Article  Google Scholar 

  14. ROSENTHAL, K. I., Quantales and Their Applications, Pitman Research Notes in Mathematics Series, Longman, 1990.

  15. WlLLE, A. M., ‘A Gentzen system for involutive residuated lattices’, Algebra Univer-salis, to appear.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Vanderbilt University, 1326 Stevenson Center, Nashville, 37240, TN, U.S.A.

    Constantine Tsinakis

  2. Department of Mathematics, Technische Universität Darmstadt, Schlossgartenstrasse 7, Darmstadt, 64289, Germany

    Annika M. Wille

Authors
  1. Constantine Tsinakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Annika M. Wille
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Constantine Tsinakis.

Additional information

Dedicated to the memory of Willem Johannes Blok

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tsinakis, C., Wille, A.M. Minimal Varieties of Involutive Residuated Lattices. Stud Logica 83, 407–423 (2006). https://doi.org/10.1007/s11225-006-8311-7

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11225-006-8311-7

Keywords

Search

Navigation