Abstract
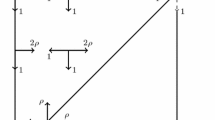
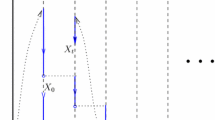
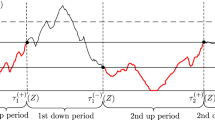
A variant of the standard symmetric system of two parallel queues under the join-the-shortest-queue policy is introduced. Here, the shortest queue has service rate \(\mu _1\), while the longest queue has rate \(\mu _2\), where \(\mu _1 + \mu _2 = 1\). In the case of equality, both queues are served at rate 1 / 2. Each queue has capacity K, which may be finite or infinite, and the global Poisson arrival rate is \(\rho \). Couplings show that, as \(\mu _2\) varies, the model is totally ordered, in terms of both total number N(t) of customers in the system and longest queue length. The two extreme cases \(\mu _2= 0\) and \(\mu _2= 1\) then provide simple stochastic bounds for N(t) for arbitrary \(\mu _2\). The ordering partially extends to the enlarged model in which, whenever the shortest queue is empty, the idle server at that queue helps—or on the contrary disturbs—the other server. The previous bounds remain valid. In the extended setup, different martingales are next built from the infinite capacity process. Those lead to simple explicit formulations of the means and Laplace transforms of the hitting time of saturation, for the process with finite K started from any initial state. Asymptotics are then derived, as K gets large. Using one particular mean time, the stationary blocking probability is explicitly obtained, extending the result by Dester et al. regarding the standard symmetric model. Finally, the joint distribution of the time and state of the system at the first queue-length equality is expressed as a function of the inverse of a simple explicit matrix.



Similar content being viewed by others
References
Adan, I., Wessels, J., Zijm, W.H.M.: Analysis of the symmetric shortest queue problem. Commun. Stat. Stoch. Models 6(4), 691–713 (1990)
Adan, I., Wessels, J., Zijm, W.H.M.: Analysis of the asymmetric shortest queue problem. Queueing Syst. 8(1), 1–58 (1991)
Adan, I., Wessels, J.: Analysis of the asymmetric shortest queue problem with threshold jockeying. Stoch. Models 7(4), 615–627 (1991)
Adan, I., Wessels, J., Zijm, W.H.M.: A compensation approach for two-dimensional Markov processes. Adv. Appl. Probab. 25(04), 783–817 (1993)
Adan, I., van Houtum, G.J., van der Wal, J.: Upper and lower bounds for the waiting time in the symmetric shortest queue system. Ann. Oper. Res. 48(2), 197–217 (1994)
Asmussen, S.: Applied Probability and Queues. Applications of Mathematics, Stochastic Modelling and Applied Probability, vol. 51. Springer, Berlin (2003)
Baccelli, F.: Exponential martingales and Wald’s formulas for two-queue networks. J. Appl. Probab. 23(3), 812–819 (1986)
Blanc, J.P.: The power-series algorithm applied to the shortest-queue model. Oper. Res. 40(1), 157–167 (1992)
Bramson, M.: Stability of join the shortest queue networks. Ann. Appl. Probab. 21(4), 1568–1625 (2011)
Braverman, A.: Steady-state analysis of the join the shortest queue model in the Halfin-Whitt regime. arXiv preprint arXiv:1801.05121 (2018)
Cohen, J.W.: A two-queue, one-server model with priority for the longer queue. Queueing Syst. 2, 261–283 (1987)
Cohen, J.W.: On entrance times of a homogeneous \(N\)-dimensional random walk: an identity. J. Appl. Probab. 25(1), 321–333 (1988)
Cohen, J.W.: Two-dimensional nearest-neighbour queueing models, a review and an example. In: Baccelli, F., Jean-Marie, A., Mitrani, I. (eds.) Quantitative Methods in Parallel Systems, pp. 141–152. Springer, Berlin (1995)
Cohen, J.W.: Analysis of the asymmetrical shortest two-server queueing model. Int. J. Stoch. Anal. 11(2), 115–162 (1998)
Conolly, B.W.: The autostrada queueing problem. J. Appl. Probab. 21(2), 394–403 (1984)
Dai, J.G., Hasenbein, J.J., Kim, B.: Stability of join-the-shortest-queue networks. Queueing Syst. 57, 129–145 (2007)
Dester, P.S., Fricker, C., Tibi, D.: Stationary analysis of the shortest queue problem. Queueing Syst. 87, 211–243 (2017)
Eschenfeldt, P., Gamarnik, D.: Join the shortest queue with many servers. The heavy traffic asymptotics. Math. Oper. Res. 43(3), 867–886 (2018)
Ethier, S.N., Kurtz, T.G.: Markov Processes: Characterization and Convergence. Wiley Series in Probability and Statistics. Wiley, London (1985)
Fayolle, G., Iasnogorodski, R.: Two coupled processors: the reduction to a Riemann–Hilbert problem. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 47(3), 325–351 (1979)
Fayolle, G., Iasnogorodski, R., Malyshev, V.: Random Walks in the Quarter Plane. Probability Theory and Stochastic Modelling, vol. 40. Springer, Berlin (2017)
Flatto, L.: The longer queue model. Probab. Eng. Inf. Sci. 3(04), 537–559 (1989)
Flatto, L., McKean, H.P.: Two queues in parallel. Commun. Pure Appl. Math. 30(2), 255–263 (1977)
Foley, R.D., McDonald, D.R.: Join the shortest queue: stability and exact asymptotics. Ann. Appl. Probab. 11(3), 569–607 (2001)
Foss, S., Chernova, N.: On the stability of a partially accessible multi-station queue with state-dependent routing. Queueing Syst. 29, 55–73 (1998)
Gertsbakh, I.: The shorter queue problem: a numerical study using the matrix-geometric solution. Eur. J. Oper. Res. 15, 374–381 (1984)
Guillemin, F., Simonian, A.: Stationary analysis of the shortest queue first service policy. Queueing Syst. 77(4), 393–426 (2014)
Haight, F.: Two queues in parallel. Biometrika 45(3–4), 401–410 (1958)
Halfin, S.: The shortest queue problem. J. Appl. Probab. 22(4), 865–878 (1985)
Kennedy, D.P.: Some martingales related to cumulative sum tests and single-server queues. Stoch. Process. Appl. 4, 261–269 (1976)
Kingman, J.: Two similar queues in parallel. Ann. Math. Stat. 32(4), 1314–1323 (1961)
Knessl, C., Yao, H.: On the finite capacity shortest queue problem. Prog. Appl. Math. 2(1), 01–34 (2011)
Knessl, C., Yao, H.: On the nonsymmetric longer queue model: Joint distribution, asymptotic properties, and heavy traffic limits. Adv. Oper. Res. (2013). https://doi.org/10.1155/2013/680539
Kurkova, I.A.: A load-balanced network with two servers. Queueing Syst. 37, 379–389 (2001)
Kurkova, I.A., Suhov, Y.M.: Malyshev’s theory and JS-queues. Asymptotics of stationary probabilities. Ann. Appl. Probab. 13(4), 1313–1354 (2003)
Li, H., Miyazawa, M., Zhao, Y.Q.: Geometric decay in a QBD process with countable background states with applications to a join-the-shortest-queue model. Stoch. Models 23(3), 413–438 (2007)
Mitzenmacher, M.: On the analysis of randomized load balancing schemes. In: Proceedings of the Ninth Annual ACM Symposium on Parallel Algorithms and Architectures, ACM, pp. 292–301 (1997)
Palmovski, Z., Rolski, T.: A technique for exponential change of measure for Markov processes. Bernoulli 8, 767–785 (2002)
Puhalskii, A.A., Vladimirov, A.A.: A large deviation principle for join the shortest queue. Math. Oper. Res. 32(3), 700–710 (2007)
Rao, B.M., Posner, M.J.M.: Algorithmic and approximation analyses of the shorter queue model. Naval Res. Logist. (NRL) 34(3), 381–398 (1987)
Ridder, A., Schwartz, A.: Large deviations without principle: join the shortest queue. Math. Methods Oper. Res. 62(3), 467–483 (2005)
Robert, P.: Stochastic Networks and Queues. Applications of Mathematics, Stochastic Modelling and Applied Probability, vol. 52. Springer, Berlin (2003)
Rogers, L.C.G., Williams, D.: Diffusions, Markov Processes and Martingales: Foundations, vol. 1. Wiley, Chichester (1994)
Tarabia, A.M.K.: Analysis of two queues in parallel with jockeying and restricted capacities. Appl. Math. Model. 32(5), 802–810 (2008)
Turner, S.R.E.: A join the shorter queue model in heavy traffic. J. Appl. Probab. 37(01), 212–223 (2000)
Turner, S.R.E.: Large deviations for join the shorter queue. Fields Inst. Commun. 28, 95–108 (2000)
Vvedenskaya, N., Dobrushin, R., Karpelevich, F.: Queueing system with selection of the shortest of two queues: an asymptotic approach. Problemy Peredachi Informatsii 32(1), 20–34 (1996)
Weber, R.R.: On the optimal assignment of customers to parallel servers. J. Appl. Probab. 15(02), 406–413 (1978)
Whitt, W.: Deciding which queue to join: some counterexamples. Oper. Res. 34(1), 55–62 (1986)
Winston, W.: Optimality of the shortest line discipline. J. Appl. Probab. 14(01), 181–189 (1977)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tibi, D. Martingales and buffer overflow for the symmetric shortest queue model. Queueing Syst 93, 153–190 (2019). https://doi.org/10.1007/s11134-019-09628-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-019-09628-9