Abstract
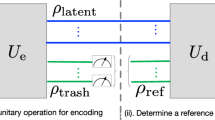
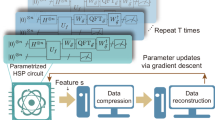
In recent experiments, the compression from qutrit to qubit is realized by the autoencoder. Inspired by the idea of dimensionality reduction, we apply the rotation transformation to compress the states. Starting from Lie algebra, we construct a 3*3 unitary matrix acting on 3*1 state and realize the rotation transformation of the states and then achieve compression of 3*1 state. Each rotation of a state is a compression, and each compression-only needs to adjust two parameters. According to the compression of 3*1 and 4*1 states by unitary matrices, we further discuss the compression law of N*1 states by unitary matrices. In the process of compression, we can adjust the form of the unitary matrix according to the system condition to change the compression position. In this paper, we focus on the compression law along the diagonal from top to bottom. We redesigned the autoencoder and added the waveplate combination to reduce the parameters without affecting the results and achieve the purpose of state compression.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Yamamura, M., Kuriyama, A., Kunihiro, T.: Schwinger-type boson realization for three sub-algebras of the su(4) algebra: the so(5), the so(4) and the su(2)\(\otimes \)su(2) algebra. Progress Theoret. Phys. 104, 385–400 (2000)
Podolsky, D., Altman, E., Rostunov, T., Demler, E.: SO(4) theory of antiferromagnetism and superconductivity in bechgaard salts. Phys. Rev. Lett. 93, 246406 (2004)
Martínez-Y-Romero, R.P., Núñez-Yépez, H.N., Salas-Brito, A.L.: Algebraic approach to radial ladder operators in the hydrogen atom. Int. J. Quantum Chem. 107, 1608–1613 (2007)
Talpaert, Y.: Mechanics in Differential Geometry. De Gruyter, Berlin, Boston (2006)
Roy, S.G., Sarkar, N.K., Bhattacharjee, R.: Determination of energy bands in solids using unitary representation of Su(1,1) lie algebra. Solid State Physics. 1447, 797–798 (2012)
Sattinger, D.H., Weaver, O.L.: Lie Group and Algebras with Applications to physics, Geometry, and Mechanics. Springer-Verlag, Berlin Heidelberg GmbH (1986)
Jen, H.H., Yip, S.-K.: Spin-incoherent luttinger liquid of one-dimensional SU(\(\kappa \)) fermions. Phys. Rev. A 98, 013623 (2018)
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Miller, G.L.: Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing, pp. 212–219. ACM, New York, USA (1996)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th, Anniversary Cambridge University Press, Cambridge, UK (2010)
Giovannetti, V., Lloyd, S., Maccone, L.: Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011)
Slussarenko, S., Weston, M.M., Chrzanowski, H.M., Shalm, L.K., Verma, V.B., Nam, S.W., Pryde, G.J.: Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 11, 700–703 (2017)
Lohani, S., Kirby, B.T., Brodsky, M., Danaci, O., Glasser, R.T.: Machine learning assisted quantum state estimation. Mach. Learn.: Sci. Technol. 1(3), 035007 (2020)
Bernien, H., Schwartz, S., Keesling, A., Levine, H., Omran, A., Pichler, H., Choi, S., Zibrov, A.S., Endres, M., Greiner, M., Vuletic, V., Lukin, M.D.: Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017)
Preskill, J.: Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018)
Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J.M., Gambetta, J.M.: Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017)
Zhang, J., Pagano, G., Hess, P.W., Kyprianidis, A., Becker, P., Kaplan, H., Gorshkov, A.V., Gong, Z.X., Monroe, C.: Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 551, 601–604 (2017)
Serre, J.P.: Lie Algebras and Lie Groups 1964 Lectures given at Harvard University. Springer-Verlag, Berlin Heidelberg (1992)
Carleo, G., Nomura, Y., Imada, M.: Constructing exact representations of quantum many-body systems with deep neural networks. Nat. Commun. 9, 1–11 (2018)
Hara, S., Ono, T., Okamoto, R., Washio, T., Takeuchi, S.: Anomaly detection in reconstructed quantum states using a machine-learning technique. Phys. Rev. A 89, 022104 (2014)
Carleo1, G., Troyer, M.: Solving the quantum many-body problem with artificial neural networks. Science. 335, 602–606 (2017)
Pepper, A., Tischler, N., Pryde, G.J.: Experimental realization of a quantum autoencoder: the compression of qutrits via machine learning. Phys. Rev. Lett. 122, 060501 (2019)
Englert, B.G., Kurtsiefer, C., Weinfurter, H.: Universal unitary gate for single-photon two-qubit states. Phys. Rev. A 63, 032303 (2001)
Acknowledgements
This work was supported in part by NSF of China (Grant Nos. 11647054 and 11505017).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Du, G., Zhou, C. & Kwek, LC. Compression and reduction of \(N*1\) states by unitary matrices. Quantum Inf Process 21, 80 (2022). https://doi.org/10.1007/s11128-022-03409-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-022-03409-9