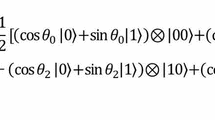Quantum image processing: the pros and cons of the techniques for the internal representation of the image. A reply to: A comment on “Quantum image processing?”

Abstract

This work demonstrates the practical infeasibility in the implementation of the techniques known as flexible representation of quantum images (and its variants) and novel enhanced quantum representation of digital images (and its variants). Besides, the implementation of the technique known as quantum Boolean image processing has proven to be extremely successful on: (a) the four main quantum simulators on the cloud, (b) two physical quantum computers, and (c) three optical tables where it also demonstrated: its resource economy and its great robustness (immunity to noise), among other advantages, in fact, without any exceptions.

Appendices

Appendix 1

Considering Eqs. (1, 2, and 4) of Sect. 3, if we call $\left| {f_{i} } \right\rangle$ to $\cos \theta_{i} \left| 0 \right\rangle + \sin \theta_{i} \left| 1 \right\rangle$, we will have,

$$ \left| {f_{i} } \right\rangle = \cos \theta_{i} \left| 0 \right\rangle + \sin \theta_{i} \left| 1 \right\rangle = \cos \theta_{i} \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right] + \sin \theta_{i} \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ {\sin \theta_{i} } \\ \end{array} } \right] , $$

(22)

where the respective density matrices for each CBS $\left| 0 \right\rangle$, and $\left| 1 \right\rangle$ will be,

$$ M_{\left| 0 \right\rangle } = \left| 0 \right\rangle \left\langle 0 \right| = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right] , {\text{ and}} $$

(23)

$$ M_{\left| 1 \right\rangle } = \left| 1 \right\rangle \left\langle 1 \right| = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right] . $$

(24)

Therefore, applying projective measurement on $\left| {f_{i} } \right\rangle$, the impact of quantum measurement [9] on FRQI is evidenced,

$$ \begin{aligned} \left| {f_{i,\left| 0 \right\rangle } } \right\rangle_{pm} & = \frac{{M_{\left| 0 \right\rangle } \left| {f_{i} } \right\rangle }}{{\sqrt {\left\langle {f_{i} } \right|M_{\left| 0 \right\rangle } M_{\left| 0 \right\rangle } \left| {f_{i} } \right\rangle } }} \\ & = \frac{{\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ {\sin \theta_{i} } \\ \end{array} } \right]}}{{\sqrt {\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } & {\sin \theta_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ {\sin \theta_{i} } \\ \end{array} } \right]} }} = \frac{{\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ 0 \\ \end{array} } \right]}}{{\sqrt {\cos^{2} \theta_{i} } }} = \frac{{\cos \theta_{i} }}{{\left| {\cos \theta_{i} } \right|}}\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right] = \left| 0 \right\rangle , \\ \end{aligned} $$

(25)

$$ \begin{aligned} \left| {f_{i,\left| 1 \right\rangle } } \right\rangle_{pm} & = \frac{{M_{\left| 1 \right\rangle } \left| {f_{i} } \right\rangle }}{{\sqrt {\left\langle {f_{i} } \right|M_{\left| 1 \right\rangle } M_{\left| 1 \right\rangle } \left| {f_{i} } \right\rangle } }} \\ & = \frac{{\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ {\sin \theta_{i} } \\ \end{array} } \right]}}{{\sqrt {\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } & {\sin \theta_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta_{i} } \\ {\sin \theta_{i} } \\ \end{array} } \right]} }} = \frac{{\left[ {\begin{array}{*{20}c} 0 \\ {\sin \theta_{i} } \\ \end{array} } \right]}}{{\sqrt {sin^{2} \theta_{i} } }} = \frac{{\sin \theta_{i} }}{{\left| {\sin \theta_{i} } \right|}}\left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] = \left| 1 \right\rangle . \\ \end{aligned} $$

(26)

That is to say, Eqs. (25) and (26) highlight the devastating effect of quantum measurement [9] on FRQI, which had already been set out in an earlier paper [4]. In this case, since FRQI encodes the colors by means of states such as those of Eq. (22), then Eqs. (25) and (26) show that the quantum measurement completely eliminates the color information of the image coded in $\left| {f_{i} } \right\rangle$, which it represents a factor of central importance into FRQI.

Appendix 2

We can use the first part of the superdense coding protocol [15] as Cl2Qu interface, Fig. 12, while as Qu2Cl interface its last part, that is, the quantum measurement along the z-axis of the Bloch’s sphere.

Fig. 12

Example of a possible pair of Cl2Qu and Qu2Cl interfaces for QuBoIP extracted from the superdense coding protocol, where $\left| {b_{1} } \right\rangle$ and $\left| {b_{2} } \right\rangle$ are the CBS version of the classic bits b₁ and b₂, respectively

Although Fig. 12 is not the most efficient option of Cl2Qu interface since one EPR pair must be prepared for each pair of bits to be transformed into their respective CBS, however, it is surely the most pedagogical, where: $\left| {\beta_{{b_{1} b_{2} }} } \right\rangle = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}\left( {\left| {b_{1} b_{2} } \right\rangle + \left( { - 1} \right)^{{b_{2} }} \left| {\overline{b}_{1} \overline{b}_{2} } \right\rangle } \right)$, while $\sigma_{x}$ and $\sigma_{z}$ are Pauli’s matrices.

The complete details of its operation can be obtained in data accessibility. The computational cost of QuBoIP is then that of the chosen Cl2Qu interface. The only case in which all bitplanes of the original image should be used is when we must invert the colors of such image. Below, we show just two of the countless examples of successful implementation of QuBoIP on a quantum platform with free access in the cloud. We chose Quirk [13] for being the most pedagogical, with an excellent drag-and-drop graphic interface. Similar implementations made on other platforms such as IBM Q [11], Rigetti [8], and Quantum Programming Studio [16] can be seen in data accessibility.