Deterministic joint remote state preparation of four-qubit cluster type with tripartite involvement | Quantum Information Processing Skip to main content

Advertisement

Springer Nature Link
Log in

Deterministic joint remote state preparation of four-qubit cluster type with tripartite involvement

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

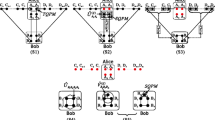
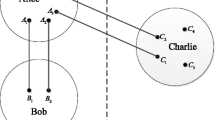
Cluster state is deemed to be a significant quantum resource, for it can encode much information; its remote preparation is significant to the quantum information processing. In the paper, a novel joint remote quantum state preparation protocol is proposed, in which three participants are included, and they are cooperatively involved for the protocol accomplishment within the configuration constructed by the four-qubit cluster type and EPR pairs. The cluster-type state is successful prepared via the appropriate unitary operations after the relevant participants perform the projection measurement. The presented protocol shows highly secure and could stand against the external eavesdropper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Hou, K.: Joint remote preparation of four-qubit cluster-type states with multiparty. Quantum Inf. Process. 12, 3821–3833 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  2. Chang, L., Zheng, S., Gu, L., Jin, L., Yang, Y.: Multiparty-controlled Joint remote preparation of an arbitrary four-qubit cluster-type state via two different entangled quantum channels. Int. J. Theor. Phys. 54, 2864–2880 (2015)

    Article  MathSciNet  Google Scholar 

  3. Wang, H., Zhou, X., An, X., Cui, M., Fu, D.: Deterministic joint remote preparation of a four-qubit cluster-type state via GHZ states. Int. J. Theor. Phys. 55(8), 3588–3596 (2016)

    Article  MathSciNet  Google Scholar 

  4. Li, W., Chen, H., Liu, Z.: Deterministic joint remote preparation of arbitrary four-qubit cluster-type state using EPR pairs. Int. J. Theor. Phys. 56(2), 351–361 (2017)

    Article  Google Scholar 

  5. Wang, D., Hoehn, R.D., Ye, L., Kais, S.: Efficient remote preparation of four-qubit cluster-type entangled states with multi-party over partially entangled channels. Int. J. Theor. Phys. 55, 3454–3466 (2016)

    Article  MathSciNet  Google Scholar 

  6. Wang, Z.: Highly efficient remote preparation of an arbitrary three-qubit state via a four-qubit cluster state and an EPR state. Quantum Inf. Process. 12, 1321–1334 (2013)

    Article  ADS  Google Scholar 

  7. Zhan, Y., Ma, P.: Deterministic joint remote preparation of arbitrary two- and three-qubit entangled states. Quantum Inf. Process. 12, 997–1009 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  8. Liu, W., Chen, Z., Liu, C., Zheng, Y.: Improved deterministic n-to-one joint remote preparation of an arbitrary qubit via EPR pairs. Int. J. Theor. Phys. 54(2), 472–483 (2015)

    Article  Google Scholar 

  9. Du, Z., Li, X.: A layered quantum communication path protocol cross multiple participants based on entanglement swapping. Quantum Inf. Process. 18(7), 226 (2019)

    Article  ADS  Google Scholar 

  10. Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67(6), 661 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  11. Hillery, M., Buzek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59(3), 1829–1834 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  12. Liu, Z.H., Chen, H.W., Liu, W.J.: Cryptanalysis of controlled quantum secure direct communication and authentication protocol based on five-particle cluster state and quantum one-time pad. Int. J. Theor. Phys. 55(10), 4564–4576 (2016)

    Article  Google Scholar 

  13. Du, Z., Li, X.: Robust high capability QKD-based database private query. Int. J. Theor. Phys. 58(2), 391–398 (2019)

    Article  Google Scholar 

  14. Xiao, H., Zhang, Z.: Subcarrier multiplexing multiple-input multiple-output quantum key distribution scheme with orthogonal quantum states. Quantum Inf. Process. 16(13), 1–18 (2017)

    ADS  MATH  Google Scholar 

  15. Cleve, R., Gottesman, D., Lo, H.K.: How to share a quantum secret. Phys. Rev. Lett. 83(3), 648 (1999)

    Article  ADS  Google Scholar 

  16. Choudhury, B.S., Samanta, S.: Perfect joint remote state preparation of arbitrary six-qubit cluster-type states. Quantum Inf. Process. 17, 175 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  17. Ma, P.-C., Chen, G.-B., Li, X.-W., Zhan, Y.-B.: Asymmetric bidirectional controlled remote preparation of an arbitrary four-qubit cluster-type state and a single-qubit state. Quantum Inf. Process. 16, 308 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  18. Shukla, C., Thapliyal, K., Pathak, A.: Hierarchical joint remote state preparation in noisy environment. Quantum Inf. Process. 16, 205 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  19. Zhang, Z.-H., Shu, L., Mo, Z.-W., Zheng, J., Ma, S.-Y., Luo, M.-X.: Joint remote state preparation between multi-sender and multi-receiver. Quantum Inf. Process. 16, 205 (2017)

    Article  ADS  Google Scholar 

  20. Hou, K., Liu, G.-H., Zhang, X.-Y., Sheng, S.-Q.: An efficient scheme for five-party quantum state sharing of an arbitrary m-qubit state using multiqubit cluster states. Quantum Inf. Process. 16, 205 (2017)

    Article  ADS  Google Scholar 

  21. Zhan, Y., Fu, H., Li, W., Ma, P.: Deterministic remote preparation of a four-qubit cluster-type entangled state. Int. J. Theor. Phys. 52, 2615–2622 (2013)

    Article  MathSciNet  Google Scholar 

  22. Devetak, I., Berger, T.: Low-entanglement remote state preparation. Phys. Rev. Lett. 87, 177901 (2001)

    Article  ADS  Google Scholar 

  23. Zeng, B., Zhang, P.: Remote-state preparation in higher dimension and the parallelizable manifold \(S^{n-1}\). Phys. Rev. A 65, 022316 (2002)

    Article  ADS  Google Scholar 

  24. Berry, D.W., Sanders, B.C.: Optimal remote state preparation. Phys. Rev. Lett. 90, 027901 (2003)

    Article  Google Scholar 

  25. Kurucz, Z., Adam, P., Janszky, J.: General criterion for oblivious remote state preparation. Phys. Rev. A 73, 062301 (2006)

    Article  ADS  Google Scholar 

  26. Buchbinder, S.D., Huang, C.L., Weinstein, Y.S.: Encoding an arbitrary state in a [7, 1, 3] quantum error correction code. Quantum Inf. Process. 12(2), 699–719 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  27. Wang, L., Zhao, S.M.: Round-robin differential-phase-shift quantum key distribution with heralded pair-coherent sources. Quantum Inf. Process. 16(4), 100 (2017)

    Article  ADS  Google Scholar 

  28. Wang, D., Ye, L.: Joint remote preparation of a class of four-qubit cluster-like states with tripartite entanglements and positive operator-valued measurements. Int. J. Theor. Phys. 52(9), 3075–3085 (2013)

    Article  MathSciNet  Google Scholar 

  29. Xiao, H., Zhang, Z.: New construction of quantum error-avoiding codes via group representation of quantum stabilizer codes. Eur. Phys. J. C 77(10), 667–680 (2017)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant No. 61672279.

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, Nanjing TECH University, Nanjing, 211800, China

    Zhenlong Du & Xiaoli Li

Authors
  1. Zhenlong Du
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaoli Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhenlong Du.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Du, Z., Li, X. Deterministic joint remote state preparation of four-qubit cluster type with tripartite involvement. Quantum Inf Process 19, 39 (2020). https://doi.org/10.1007/s11128-019-2535-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-019-2535-8

Keywords