Discrete-time quantum walk on the Cayley graph of the dihedral group

Abstract

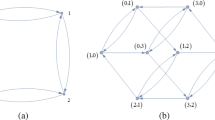
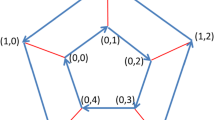
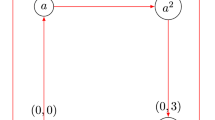
The finite dihedral group generated by one rotation and one flip is the simplest case of the non-Abelian group. Cayley graphs are diagrammatic counterparts of groups. In this paper, much attention is given to the Cayley graph of the dihedral group. Considering the characteristics of the elements in the dihedral group, we conduct the model of discrete-time quantum walk on the Cayley graph of the dihedral group by special coding mode. This construction makes Fourier transformation be used to carry out spectral analysis of the dihedral quantum walk, i.e. the non-Abelian case. Furthermore, the relation between quantum walk without memory on the Cayley graph of the dihedral group and quantum walk with memory on a cycle is discussed, so that we can explore the potential of quantum walks without and with memory. Here, the numerical simulation is carried out to verify the theoretical analysis results and other properties of the proposed model are further studied.

Appendix: probability distribution of quantum walk with memory on a cycle

Here, we make a simple description of probability distribution and the time-averaged value of the walk referred to Ref. [37].

In quantum walk with memory on a cycle, the initial state of the walk is $\left| {{\phi _0}} \right\rangle$ and the vector of amplitudes is $\varPhi \left( {n,0} \right)$. In the Fourier basis, the initial state is ${\tilde{\varPhi }} \left( {k,0} \right)$, for any $k = 0, \ldots ,d - 1$, where d is the number of vertices. And the form of the amplitudes after t steps can be calculated and the vector of the amplitudes is

$$\begin{aligned} {\tilde{\varPhi }} \left( {k,t} \right) = M_k^t{\tilde{\varPhi }} \left( {k,0} \right) , \end{aligned}$$

(32)

for any k. The initial state of the walk ${\tilde{\varPhi }} \left( {k,0} \right)$ can be written as ${\tilde{\varPhi }} \left( {k,0} \right) = \sum \limits _{i = 1}^4 {{\alpha _i}\left( k \right) {v_i}\left( k \right) }$ in the ${\left\{ {{v_i}} \right\} _{i = 1, \ldots ,4}}$ basis, where ${\alpha _i}\left( k \right) = \left( {{v_i}\left( k \right) ,{\tilde{\varPhi }} \left( {k,0} \right) } \right)$ are components of ${{\tilde{\varPhi }} \left( {k,0} \right) }$ in the ${\left\{ {{v_i}} \right\} _{i = 1, \ldots ,4}}$ basis. Thus, the evolution in the Fourier basis can be written as

$$\begin{aligned} {\tilde{\varPhi }} \left( {k,t} \right) = M_k^t\sum \limits _{i = 1}^4 {{\alpha _i}\left( k \right) {v_i}\left( k \right) } = \sum \limits _{i = 1}^4 {{\alpha _i}\left( k \right) \lambda _i^t\left( k \right) {v_i}\left( k \right) }, \end{aligned}$$

(33)

where ${\lambda _i}$ and ${v_i}$ are the eigenvalues and eigenvectors, respectively.

The original components can be expressed by the Fourier-transformed vectors as

$$\begin{aligned} \varPhi \left( {n,t} \right) = \frac{1}{d}\sum \limits _{k = 0}^{d - 1} {{e^{\frac{{2\pi ikn}}{d}}}{\tilde{\varPhi }} \left( {k,t} \right) } = \frac{1}{d}\sum \limits _{k = 0}^{d - 1} {\sum \limits _{j = 1}^4 {{e^{\frac{{2\pi ikn}}{d}}}{\alpha _j}\left( k \right) \lambda _j^t\left( k \right) {v_j}\left( k \right) } }. \end{aligned}$$

(34)

Therefore, the probability of finding the particle at the nth node after t steps is

$$\begin{aligned} p\left( {n,t} \right)= & {} {\left| {\varPhi \left( {n,t} \right) } \right| ^2}\nonumber \\= & {} \frac{1}{{{d^2}}}\sum \limits _{k,m = 0}^{d - 1} {\sum \limits _{j,l = 1}^4 {{e^{\frac{{2\pi i\left( {m - k} \right) n}}{d}}}\alpha _j^*\left( k \right) {\alpha _l}\left( m \right) v_j^\dag \left( k \right) {v_l}\left( m \right) {{\left[ {\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) } \right] }^t}} } . \nonumber \\ \end{aligned}$$

(35)

Time-averaged probability distribution is

$$\begin{aligned} {\bar{p}}\left( n \right)= & {} \mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{t}\sum \limits _{s = 0}^{t - 1} {p\left( {n,s} \right) } \nonumber \\= & {} \frac{1}{{{d^2}}}\sum \limits _{k,m = 0}^{d - 1} {\sum \limits _{j,l = 1}^4 {{e^{\frac{{2\pi i\left( {m - k} \right) n}}{d}}}\alpha _j^*\left( k \right) {\alpha _l}\left( m \right) v_j^\dag \left( k \right) {v_l}\left( m \right) \mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{t}\sum \limits _{s = 0}^{t - 1} {{{\left[ {\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) } \right] }^s}} } } . \nonumber \\ \end{aligned}$$

(36)

One can observe that the convergence of ${\bar{p}}\left( n \right)$ depends only on the behavior of the term

$$\begin{aligned} {\mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{t}\sum \limits _{s = 0}^{t - 1} {{{\left[ {\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) } \right] }^s}} }. \end{aligned}$$

(37)

If ${\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) = 1}$, $\mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{t}\sum \limits _{s = 0}^{t - 1} {{{\left[ {\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) } \right] }^s}} = 1$, otherwise 0. Unfortunately, any further simplifications of Eqs. (35) and (36) were not possible. However, definition of $\mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{t}\sum \limits _{s = 0}^{t - 1} {{{\left[ {\lambda _j^*\left( k \right) {\lambda _l}\left( m \right) } \right] }^s}}$ can be easily calculated using the standard computer algebra systems and thus allows for the evaluation of Eq. (36).