An Updatable Classifier Diversity Measure Based on the ER Rule | Neural Processing Letters Skip to main content
Springer Nature Link
Log in

An Updatable Classifier Diversity Measure Based on the ER Rule

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

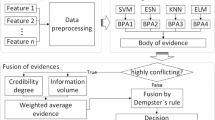
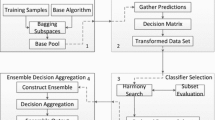
Abstract

In ensemble learning, accuracy and diversity among classifiers are the keys to good integration. However, most diversity measures only evaluate the diversity of classifiers from a single point of view and have a poor correlation with the generalization capability of the final model. As such, there is still a lack of an effective diversity measure to guide the integration of classifiers. In this paper, an updatable fusion measure is proposed to evaluate diversity in classifiers. It is based on the evidential reasoning rule by fusing various measures from multiple perspectives. Before the fusion, the correlation among various diversity measures is tested. Only those measures with weak correlation can be fused. In addition, whenever a new effective measure appears, it can be fused with the old fusion measure after the significance test. Through the experimental verification of multiple data sets, classifiers, and combination strategies, this measure can effectively reflect the diversity of classifier combinations and assist classifier integration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Dietterich TG (1997) Machine learning research: four current directions. AI Mag 18(4):97–136

    Google Scholar 

  2. Zhou ZH, Wu J, Tang W (2002) Ensembling neural networks: Many could be better than all. Artif Intell 137(1–2):239–263

    Article  MathSciNet  Google Scholar 

  3. Sun B, Wang JD, Chen HY (2014) Diversity measures in ensemble learning. Control Decision 29(03):385–395

    MATH  Google Scholar 

  4. Jiang ZS, Liu HZ, Fu B (2019) Decomposition theories of generalization error and AUC in ensemble learning with application in weight optimization. Chin J Comput 042(001):1–15

    Google Scholar 

  5. Yang C, Yin XC, Hao HW (2014) Classifier ensemble with diversity: effactiveness analysis and ensemble optimization. Acta Automatica Sinica 40(004):660–674

    MathSciNet  Google Scholar 

  6. Brown G, Wyatt J, Harris R (2005) Diversity creation methods: a survey and categorisation. Informat Fusion 6(1):5–20

    Article  Google Scholar 

  7. Guo D, Jin Y, Ding J (2018) Heterogeneous ensemble-based infill criterion for evolutionary multiobjective optimization of expensive problems. IEEE Trans Cybernet 99:1–14

    Google Scholar 

  8. Pividori M, Stegmayer G, Milone DH (2016) Diversity control for improving the analysis of consensus clustering. Inf Sci 361–362:120–134

    Article  Google Scholar 

  9. Jackowski K (2018) New diversity measure for data stream classification ensembles. Eng Appl Artif Intell 74:23–34

    Article  Google Scholar 

  10. Jurek A, Hong J, Chi Y (2017) A novel ensemble learning approach to unsupervised record linkage. Informat Syst 71

  11. Kuncheva LI, Whitaker CJ (2003) Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy. Mach Learn 51(2):181–207

    Article  Google Scholar 

  12. Liu H, Du Y, Wu Z (2019) AEM: attentional ensemble model for personalized classifier weight learning. Pattern Recogn 96:106976

    Article  Google Scholar 

  13. Zhou G, Guo LF (2019) Process diversity measurement of ensemble learning based on information entropy. Comp Eng Sci 41(9):8

    Google Scholar 

  14. Tang EK, Suganthan PN, Yao X (2006) An analysis of diversity measures. Mach Learn 65(1):247–271

    Article  Google Scholar 

  15. Li Y, Zhao M, Meng-Yao Xu (2019) A survey of research on multi-source information fusion technology. Intell Comput Appl. 9(5):4

    Google Scholar 

  16. Durrant-Whyte H, Henderson TC (2016) Multisensor data fusion[M]. Springer, Handbook of Robotics, pp 585–610

    Google Scholar 

  17. Zhu H, Basir O (2006) A novel fuzzy evidential reasoning paradigm for data fusion with applications in image processing[J]. Soft Comput 10(12):1169–1180

    Article  Google Scholar 

  18. Wang H, Chen Y (2006) Sensor Data fusion using rough set for mobile robots system. IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications. 1–5.

  19. Yang JB, Xu DL (2013) Evidential reasoning rule for evidence combination. Artif Intell 205(1):1–29

    Article  MathSciNet  Google Scholar 

  20. Tumer K, Ghosh J (1996) Analysis of decision boundaries in linearly combined neural classifiers. Pattern Recogn 29(2):341–348

    Article  Google Scholar 

  21. Zhou ZH (2012) Ensemble methods: foundations and algorithms[M]. Taylor & Francis, China

    Book  Google Scholar 

  22. Shipp CA, Kuncheva LI (2002) Relationships between combination methods and measures of diversity in combining classifiers. Informat Fusion 3(2):135–148

    Article  Google Scholar 

  23. Yule GU (1900) On the association of attributes in statistics. Philos Trans Royal Soci A 194:257–319

    MATH  Google Scholar 

  24. Giacinto G, Roli F (2000) Design of effective neural network ensembles for image classification processes. Image Vision Comput J 19:699–707

    Article  Google Scholar 

  25. Partridge D, Krzanowski WJ (1997) Software diversity: practical statistics for its measurement and exploitation. Inf Softw Technol 39(10):707–717

    Article  Google Scholar 

  26. Jousselme AL, Grenier D (2001) A new distance between two bodies of evidence. Informat Fusion 2(2):91–101

    Article  Google Scholar 

  27. Yang Y, Han DQ, Han CZ (2012) A difference measure of multi-classifier basedon evidence distance. J Aviat 33(006):1093–1099

    Google Scholar 

  28. Banfield RE, Hall LO, Bowyer KW (2003) A new ensemble diversity measure applied to thinning ensembles[C]. In: Proceedings of the 4th international workshop on multiple classifier systems. Berlin, Springer-Verlag, pp 306–316

    Chapter  Google Scholar 

  29. Melville P, Mooney R (2003) Constructing diverse classifier ensembles using artificial training examples. In: Proceedings of the eighteenth international joint conference on artificial intelligence. Mexico, pp 505–510

  30. Gao Q, Xu DL (2018) An empirical study on the application of the evidential reasoning rule to decision making in financial investment. Knowledge-Based Syst 164

  31. Zhou M, Liu XB, Chen YW (2018) Evidential reasoning rule for MADM with both weights and reliabilities in group decision making. Knowledge-Based Syst 2018(143):142–161

    Article  Google Scholar 

  32. Xu XB, Zheng J, Xu DL (2015) Information fusion fault diagnosis method based on evidential reasoning rule. Control Theor Appl 32(9):1170–1182

    Google Scholar 

  33. Tang SW, Zhou ZJ, Hu CH (2020) A new evidential reasoning rule-based safety assessment method with sensor reliability for complex systems. IEEE Trans Cybernet (99)

  34. Zhao FJ, Zhou ZJ, Hu CH, Chang LL, Zhou ZG, Li GL (2016) A new evidential reasoning-based method for online safety assessment of complex systems. IEEE Transact Syst Man Cybernet 99:1–13

    Google Scholar 

  35. Martinez-Munoz G, Hernandez-Lobato D, Suarez A (2009) An analysis of ensemble pruning techniques based on ordered aggregation. IEEE Trans Pattern Anal Mach Intell 31(2):245–259

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the Postdoctoral Science Foundation of China under Grant No. 2020M683736, in part by the Natural Science Foundation of Heilongjiang Province of China under Grant No. LH2021F038, in part by the innovation practice project of college students in Heilongjiang Province under Grant No. 202010231009, 202110231024, 202110231155, in part by the graduate quality training and improvement project of Harbin Normal University under Grant No. 1504120015, in part by the graduate academic innovation project of Harbin Normal University under Grant No. HSDSSCX2021-120, HSDSSCX2021-29

Author information

Authors and Affiliations

  1. Harbin Normal University, Harbin, 150025, China

    Cong Xu, Wei He & Hai-Long Zhu

  2. Rocket Force University of Engineering, Xi’an, 710025, China

    Shuai-Wen Tang & Wei He

Authors
  1. Cong Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuai-Wen Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hai-Long Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei He.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, C., Tang, SW., He, W. et al. An Updatable Classifier Diversity Measure Based on the ER Rule. Neural Process Lett 54, 4247–4263 (2022). https://doi.org/10.1007/s11063-022-10807-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-10807-8

Keywords

Search

Navigation