Stick-Breaking Dependent Beta Processes with Variational Inference

Abstract

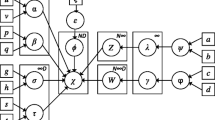
The beta processes (BP) is a powerful nonparametric tool in feature learning, which is often used as the prior of Bernoulli process for choosing features from a feature dictionary. However, it still shows a limitation in processing some real-world data, as the stood and BP is independent of data. In practice, the probabilities of selecting features in the latent space for different observed data are different, and they are usually dependent on some information from data, such as the location or time information. For example, data with closer distances usually have similar features. This kind of information (location or time) often called covariates, which are ignored in most BP-related literature. To account this problem, we propose a variational inference based dependent beta processes (VDBP), in which the dependent beta process is constructed using the stick-breaking representation and the dependency on the covariates is captured by a Gaussian process prior. An elegant representation of variational inference for with VDBP prior is obtained, which offers the efficient training method for the models using VDBP as priors. Through instantiating a Bayesian factor analysis model with VDBP, we verify the effectiveness of the proposed VDBP in image denoising and image inpainting tasks.