Robust Stability of Inertial BAM Neural Networks with Time Delays and Uncertainties via Impulsive Effect | Neural Processing Letters Skip to main content
Springer Nature Link
Log in

Robust Stability of Inertial BAM Neural Networks with Time Delays and Uncertainties via Impulsive Effect

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

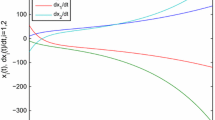
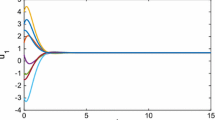
This paper investigates the robust stability of inertial bidirectional association memory (BAM) neural networks with time delays and uncertainties via impulsive control. Firstly, utilizing suitable variable substitution, the seconded-order inertial BAM neural networks can be transformed into first-order differential equations. Secondly, Under the framework of Lyapunov stability method, Halanay inequality and impulsive differential inequations, we develop some techniques of impulsive to achieve the robust stability of inertial BAM neural networks. These obtained criteria are capable of reducing computational burden in the theoretical part. Some effective sufficient conditions are established for the realization of stability of the underlying network. Finally, an illustrative example is given to verify the validity of the obtained results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wen S, Zeng Z, Huang T (2014) Observer-based synchronization of memristive systems with multiple networked input and output delays. Nonlinear Dyn 78(1):541–554

    Article  MathSciNet  MATH  Google Scholar 

  2. Li C, Yu X, Huang T et al (2016) A generalized Hopfield network for nonsmooth constrained convex optimization: Lie derivative approach. IEEE Trans Neural Netw Learn Syst 27(2):308–321

    Article  MathSciNet  Google Scholar 

  3. Wen S, Zeng Z, Huang T et al (2014) Exponential adaptive lag synchronization of memristive neural networks via fuzzy method and applications in pseudorandom number generators. IEEE Trans Fuzzy Syst 22(6):1704–1713

    Article  Google Scholar 

  4. Li C, Yu X, Liu ZW et al (2016) Asynchronous impulsive containment control in switched multi-agent systems. Inf Sci 370–371:667–679

    Article  Google Scholar 

  5. Li C, Yu X, Yu W et al (2016) Distributed event-triggered scheme for economic dispatch in smart grids. IEEE Trans Industr Inf. doi:10.1109/TII.2015.2479558

    Google Scholar 

  6. Zhang W, Tang Y, Miao Q et al (2013) Exponential synchronization of coupled switched neural networks with mode-dependent impulsive effects. IEEE Trans Neural Netw Learn Syst 24(8):1316–1326

    Article  Google Scholar 

  7. Cochocki A, Unbehauen R (1993) Neural networks for optimization and signal processing. Wiley, Hoboken

    Google Scholar 

  8. Nakaguchi T, Apos JIN, No K et al (2002) A novel architecture using hysteresis neural networks for solving combinatorial optimization problems. IEICE technical report. Neurocomputing 101:155–160

    Google Scholar 

  9. Kwok T, Smith KA (1999) A unified framework for chaotic neural-network approaches to combinatorial optimization. IEEE Trans Neural Networks 10(4):978–981

    Article  Google Scholar 

  10. Sobue S, Yamai K, Ito M et al(2014) Progress monitoring of construction projects using neural networks pattern recognition. Construction Research Congress 2009@sBuilding a Sustainable Future. ASCE, pp 1068–1078

  11. Carpenter GA (1989) Neural network models for pattern recognition and associative memory. Neural Netw 2(4):243–257

    Article  Google Scholar 

  12. Wen S, Huang T, Zeng Z et al (2015) Circuit design and exponential stabilization of memristive neural networks. Neural Netw 63(3):48–56

    Article  MATH  Google Scholar 

  13. Velmurugan G, Rakkiyappan R, Cao J (2016) Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw 73:36–46

    Article  MATH  Google Scholar 

  14. Li S, Cao J, He Y (2016) Pinning controllability scheme of directed complex delayed dynamical networks via periodically intermittent control. Discrete Dyn Nat Soc 2016:1–10

    MathSciNet  Google Scholar 

  15. Li X, Song S (2014) Research on synchronization of chaotic delayed neural networks with stochastic perturbation using impulsive control method. Commun Nonlinear Sci Numer Simul 19(10):3892–3900

    Article  MathSciNet  Google Scholar 

  16. He X, Li C, Huang T et al (2014) A recurrent neural network for solving bilevel linear programming problem. IEEE Trans Neural Netw Learn Syst 25(4):824–830

    Article  Google Scholar 

  17. Li H, Liao X, Lei X et al (2013) Second-order consensus seeking in multi-agent systems with nonlinear dynamics over random switching directed networks. IEEE Trans Circ Syst I Regul Pap 60(6):1595–1607

    Article  MathSciNet  Google Scholar 

  18. Rakkiyappan R, Dharani S, Zhu Q (2015) Synchronization of reaction-diffusion neural networks with time-varying delays via stochastic sampled-data controller. Nonlinear Dyn 79(1):485–500

    Article  MathSciNet  MATH  Google Scholar 

  19. Li H, Liao X, Huang T et al (2015) Event-triggering sampling based leader-following consensus in second-order multi-agent systems. IEEE Trans Autom Control 60(7):1998–2003

    Article  MathSciNet  MATH  Google Scholar 

  20. Li H, Liao X, Huang T et al (2015) Second-order global consensus in multiagent networks with random directional link failure. IEEE Trans Neural Netw Learn Syst 26(3):565–575

    Article  MathSciNet  Google Scholar 

  21. Li H, Chen G, Huang T et al (2016) Event-triggered distributed average consensus over directed digital networks with limited communication bandwidth. IEEE Trans Cybern. doi:10.1109/TCYB.2015.2496977

    Google Scholar 

  22. Jagger DJ, Ashmore JF (1999) The fast activating potassium current, I K, f, in guinea-pig inner hair cells is regulated by protein kinase A. Neurosci Lett 263(2):145–148

    Article  Google Scholar 

  23. Ospeck M, Eguíluz VM, Magnasco MO (2001) Evidence of a Hopf bifurcation in frog hair cells. Biophys J 80(6):2597–2607

    Article  Google Scholar 

  24. He X, Li C, Shu Y (2012) Bogdanov–Takens bifurcation in a single inertial neuron model with delay. Neurocomputing 89:193–201

    Article  Google Scholar 

  25. Tu Z, Cao J, Hayat T (2016) Matrix measure based dissipativity analysis for inertial delayed uncertain neural networks. Neural Netw 75:47–55

    Article  Google Scholar 

  26. Wei X (2013) Exponential stability of periodic solutions for inertial Cohen–Grossberg-type BAM neural networks with time delays. WSEAS Trans Math 12(2):159–169

    Google Scholar 

  27. Tani J (1996) Model-based learning for mobile robot navigation from the dynamical systems perspective. IEEE Trans Syst Man Cybern B 26(3):421–436

    Article  Google Scholar 

  28. Cao J, Wan Y (2014) Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Neural Netw 53:165–172

    Article  MATH  Google Scholar 

  29. Xu C, Zhang Q (2015) Existence and global exponential stability of anti-periodic solutions for BAM neural networks with inertial term and delay. Neurocomputing 153:108–116

    Article  Google Scholar 

  30. Hu J, Cao J, Alofi A et al (2015) Pinning synchronization of coupled inertial delayed neural networks. Cogn Neurodyn 9(3):341–350

    Article  Google Scholar 

  31. Tu Z, Cao J, Hayat T (2016) Global exponential stability in Lagrange sense for inertial neural networks with time-varying delays. Neurocomputing 171:524–531

    Article  Google Scholar 

  32. Liu X, Zhang K, Xie WC (2016) Pinning impulsive synchronization of reaction-siffusion neural networks with time-varying delays. IEEE Trans Neural Netw Learn Syst. doi:10.1109/TNNLS.2016.2518479

    Google Scholar 

  33. Zhu Q, Cao J (2010) Robust exponential stability of Markovian jump impulsive stochastic Cohen–Grossberg neural networks with mixed time delays. IEEE Trans Neural Netw 21(8):1314–1325

    Article  Google Scholar 

  34. Yang X, Cao J, Lu J (2012) Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control. IEEE Trans Circ Syst I Regul Pap 59(2):371–384

    Article  MathSciNet  Google Scholar 

  35. Yang X, Cao J, Yang Z (2013) Synchronization of coupled reaction-diffusion neural networks with time-varying delays via pinning-impulsive controller. SIAM J Control Optim 51(5):3486–3510

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhang H, Ma T, Huang GB et al (2010) Robust global exponential synchronization of uncertain chaotic delayed neural networks via dual-stage impulsive control. IEEE Trans Syst Man Cybern B Cybern 40(3):831–844

    Article  Google Scholar 

  37. Huang T, Li C et al (2012) Robust exponential stability of uncertain delayed neural networks with stochastic perturbation and impulse effects. IEEE Trans Neural Netw Learn Syst 23:866–875

    Article  Google Scholar 

  38. Guan ZH, Chen G (1999) On delayed impulsive Hopfield neural networks. Neural Netw 12(2):273–280

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by Fundamental Research Funds for the Central Universities (Grant Nos. XDJK2016BC137, SWU116004), Natural Science Foundation of China (Grant Nos. 61374078, 61403313, 61633011). This publication was made possible by NPRP Grant # NPRP 7-1482-1-278 from the Qatar National Research Fund (a member of Qatar Foundation).

Author information

Authors and Affiliations

  1. School of Electronics and Information Engineering, Southwest University, Chongqing, 400715, People’s Republic of China

    Wei Zhang & Chuandong Li

  2. Key Laboratory of Machine Perception and Children’s Intelligence Development, Chongqing University of Education, Chongqing, 400067, People’s Republic of China

    Wei Zhang

  3. Department of Mathematics, Texas A&M University at Qatar, P.O. Box 23874, Doha, Qatar

    Tingwen Huang

  4. College of Computer Science and Technology, Guizhou University, Guiyang, 550025, People’s Republic of China

    Jing Yang

Authors
  1. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tingwen Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chuandong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jing Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tingwen Huang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, W., Huang, T., Li, C. et al. Robust Stability of Inertial BAM Neural Networks with Time Delays and Uncertainties via Impulsive Effect. Neural Process Lett 48, 245–256 (2018). https://doi.org/10.1007/s11063-017-9713-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-017-9713-4

Keywords

Search

Navigation