Comment on “On Discriminative vs. Generative Classifiers: A Comparison of Logistic Regression and Naive Bayes”

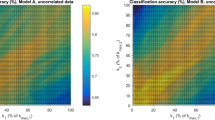
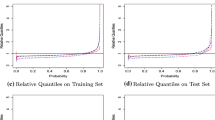
Abstract

Comparison of generative and discriminative classifiers is an ever-lasting topic. As an important contribution to this topic, based on their theoretical and empirical comparisons between the naïve Bayes classifier and linear logistic regression, Ng and Jordan (NIPS 841–848, 2001) claimed that there exist two distinct regimes of performance between the generative and discriminative classifiers with regard to the training-set size. In this paper, our empirical and simulation studies, as a complement of their work, however, suggest that the existence of the two distinct regimes may not be so reliable. In addition, for real world datasets, so far there is no theoretically correct, general criterion for choosing between the discriminative and the generative approaches to classification of an observation x into a class y; the choice depends on the relative confidence we have in the correctness of the specification of either p(y|x) or p(x, y) for the data. This can be to some extent a demonstration of why Efron (J Am Stat Assoc 70(352):892–898, 1975) and O’Neill (J Am Stat Assoc 75(369):154–160, 1980) prefer normal-based linear discriminant analysis (LDA) when no model mis-specification occurs but other empirical studies may prefer linear logistic regression instead. Furthermore, we suggest that pairing of either LDA assuming a common diagonal covariance matrix (LDA-Λ) or the naïve Bayes classifier and linear logistic regression may not be perfect, and hence it may not be reliable for any claim that was derived from the comparison between LDA-Λ or the naïve Bayes classifier and linear logistic regression to be generalised to all generative and discriminative classifiers.