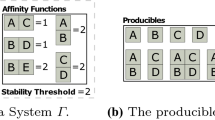
Abstract
The theme of this paper is computation in Winfree’s Abstract Tile Assembly Model (TAM). We first review a simple, well-known tile assembly system (the “wedge construction”) that is capable of universal computation. We then extend the wedge construction to prove the following result: if a set of natural numbers is decidable, then it and its complement’s canonical two-dimensional representation self-assemble. This leads to a novel characterization of decidable sets of natural numbers in terms of self-assembly. Finally, we show that our characterization is robust with respect to various (restrictive) geometrical constraints.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Adleman L, Cheng Q, Goel A, Huang M-D (2001) Running time and program size for self-assembled squares. In: STOC ’01: proceedings of the thirty-third annual ACM symposium on theory of computing. ACM, New York, pp 740–748
Adleman LM, Kari J, Kari L, Reishus D, Sosík P (2009) The undecidability of the infinite ribbon problem: implications for computing by self-assembly. SIAM J Comput 38(6):2356–2381
Barish RD, Schulman R, Rothemund PW, Winfree E (2009) An information-bearing seed for nucleating algorithmic self-assembly. Proc Natl Acad Sci USA 106(15):6054–6059
Becker F, Rapaport I, Rémila E (2006) Self-assembling classes of shapes with a minimum number of tiles, and in optimal time. In: Foundations of software technology and theoretical computer science (FSTTCS), pp 45–56
Cheng Q, Goel A, de Espanés PM (2004) Optimal self-assembly of counters at temperature two. In: Proceedings of the first conference on foundations of nanoscience: self-assembled architectures and devices
Cheng Q, Aggarwal G, Goldwasser MH, Kao M-Y, Schweller RT, de Espanés PM (2005) Complexities for generalized models of self-assembly. SIAM J Comput 34:1493–1515
Demaine ED, Demaine ML, Fekete SP, Ishaque M, Rafalin E, Schweller RT, Souvaine DL (2008) Staged self-assembly: nanomanufacture of arbitrary shapes with O(1) glues. Nat Comput 7(3):347–370
Doty D (2009) Randomized self-assembly for exact shapes. In: Proceedings of the fiftieth IEEE conference on foundations of computer science (FOCS)
Doty D, Patitz MJ (2009) A domain specific language for programming in the tile assembly model. In: Proceedings of the fifteenth international meeting on DNA computing and molecular programming, Fayetteville, Arkansas, USA, June 8–11, 2009, pp 25–34
Doty D, Patitz MJ, Summers SM Limitations of self-assembly at temperature 1. Theor Comput Sci (to appear)
Fu Y, Schweller R (2009) Temperature 1 self-assembly: deterministic assembly in 3D and probabilistic assembly in 2D. Technical report 0912.0027, Computing Research Repository
Kao M-Y, Schweller RT (2007) Reducing tile complexity for self-assembly through temperature programming. In: Proceedings of the 17th annual ACM-SIAM symposium on discrete algorithms (SODA 2006), Miami, FL, January 2006, pp 571–580
Kao M-Y, Schweller RT (2008) Randomized self-assembly for approximate shapes. In: International colloqium on automata, languages, and programming (ICALP). Lecture notes in computer science, vol 5125. Springer, pp 370–384
Lathrop JI, Lutz JH, Summers SM (2009) Strict self-assembly of discrete Sierpinski triangles. Theor Comput Sci 410:384–405
Lathrop JI, Lutz JH, Patitz MJ, Summers SM Computability and complexity in self-assembly. Theory Comput Syst (to appear)
Patitz MJ (2009) Simulation of self-assembly in the abstract tile assembly model with ISU TAS. In: 6th Annual conference on foundations of nanoscience: self-assembled architectures and devices, Snowbird, UT, USA, 20–24 April 2009
Reif JH (1999) Local parallel biomolecular computing. DNA based computers III, vol 48 of DIMACS. American Mathematical Society, pp 217–254
Rothemund PWK (2001) Theory and experiments in algorithmic self-assembly. Ph.D. thesis, University of Southern California
Rothemund PWK, Winfree E (2000) The program-size complexity of self-assembled squares (extended abstract). In: STOC ’00: Proceedings of the thirty-second annual ACM symposium on theory of computing, New York, NY, USA. ACM, pp 459–468
Rothemund PWK, Papadakis N, Winfree E (2004) Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol 2(12):2041–2053
Soloveichik D, Winfree E (2007) Complexity of self-assembled shapes. SIAM J Comput 36(6):1544–1569
Wang H (1961) Proving theorems by pattern recognition—II. Bell Syst Tech J XL(1):1–41
Wang H (1963) Dominoes and the AEA case of the decision problem. In: Proceedings of the symposium on mathematical theory of automata, New York, 1962. Polytechnic Press of Polytechnic Inst. of Brooklyn, Brooklyn, pp 23–55
Winfree E (1998) Algorithmic self-assembly of DNA. Ph.D. thesis, California Institute of Technology
Acknowledgments
Both authors wish to thank David Doty, Jack Lutz and Damien Woods for useful discussions. This research was supported in part by National Science Foundation Grants 0652569 and 0728806. A preliminary version of this research was presented at the Sixth International Conference on Unconventional Computation, August 25–28 2008, Vienna, Austria. Scott M. Summers’s research was supported in part by NSF-IGERT Training Project in Computational Molecular Biology Grant number DGE-0504304.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Patitz, M.J., Summers, S.M. Self-assembly of decidable sets. Nat Comput 10, 853–877 (2011). https://doi.org/10.1007/s11047-010-9218-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-010-9218-9