A Practical Method for Designing Linear Quadratic Regulator for Commensurate Fractional-Order Systems | Journal of Optimization Theory and Applications
Skip to main content
Springer Nature Link
Log in

A Practical Method for Designing Linear Quadratic Regulator for Commensurate Fractional-Order Systems

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

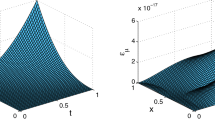
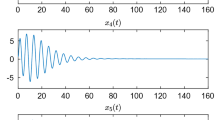
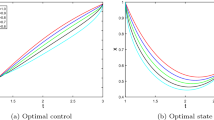
The methods currently available for designing a linear quadratic regulator for fractional-order systems are either based on sufficient-type conditions for the optimality of functionals or generate very complicated analytical solutions even for simple systems. It follows that the use of such methods is limited to very simple problems. The present paper proposes a practical method for designing a linear quadratic regulator (assuming linear state feedback), Kalman filter, and linear quadratic Gaussian regulator/controller for commensurate fractional-order systems (in Caputo sense). For this purpose, considering the fact that in dealing with fractional-order systems the cost function of linear quadratic regulator has only one extremum, the optimal state feedback gains of linear quadratic regulator and the gains of the Kalman filter are calculated using a gradient-based numerical optimization algorithm. Various fractional-order linear quadratic regulator and Kalman filter design problems are solved using the proposed approach. Specifically, a linear quadratic Gaussian controller capable of tracking step command is designed for a commensurate fractional-order system which is non-minimum phase and unstable and has seven (pseudo) states.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Caponetto, R., Dongola, G., Fortuna, L., Petras, I.: Fractional Order Systems: Modeling and Control Applications. World Scientific, London (2010)

    Book  Google Scholar 

  2. Aghababa, M.P.: Fractional modeling and control of a complex nonlinear energy supply-demand system. Complexity 20, 74–86 (2015)

    Article  MathSciNet  Google Scholar 

  3. Lewandowski, R., Chorazyczewski, B.: Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 88, 1–17 (2010)

    Article  Google Scholar 

  4. Bode, H.W.: Network Analysis and Feedback Amplifier Design. Van Nostrand, New York (1945)

    Google Scholar 

  5. Oustaloup, A., Mathieu, B., Lanusse, P.: The CRONE control of resonant plants: application to a flexible transmission. Eur. J. Control 1, 113–121 (1995)

    Article  Google Scholar 

  6. Podlubny, I.: Fractional-order systems and \(PI^\lambda D^\mu \)-controllers. IEEE Trans. Automat. Contr. 44, 208–214 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  7. Merrikh-Bayat, F.: General rules for optimal tuning the \(PI^\lambda D^\mu \) controllers with application to first-order plus time delay processes. Can. J. Chem. Eng. 90, 1400–1410 (2012)

    Article  Google Scholar 

  8. El-Khazali, R.: Fractional-order \(PI^\lambda D^\mu \) controller design. Comput. Math. Appl. 66, 639–646 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Vu, T.N.L., Lee, M.: Analytical design of fractional-order proportional-integral controllers for time-delay processes. ISA Trans. 52, 583–591 (2013)

    Article  Google Scholar 

  10. Luo, Y., Chen, Y.Q., Wang, C.Y., Pi, Y.G.: Tuning fractional order proportional integral controllers for fractional order systems. J. Process Control 20, 823–831 (2010)

    Article  Google Scholar 

  11. Merrikh-Bayat, F., Karimi-Ghartemani, M.: Method for designing \(PI^\lambda D^\mu \) stabilisers for minimum-phase fractional-order systems. IET Control Theory Appl. 4, 61–70 (2010)

    Article  MathSciNet  Google Scholar 

  12. Beschi, M., Padula, F., Visioli, A.: Fractional robust PID control of a solar furnace. Control Eng. Pract. 56, 190–199 (2016)

    Article  Google Scholar 

  13. Zhang, M., Lin, X., Yin, W.: An improved tuning method of fractional order proportional differentiation (FOPD) controller for the path tracking control of tractors. Biosyst. Eng. 116, 478–486 (2013)

    Article  Google Scholar 

  14. Chao, H., Luo, Y., Di, L., Chen, Y.Q.: Roll-channel fractional order controller design for a small fixed-wing unmanned aerial vehicle. Control Eng. Pract. 18, 761–772 (2010)

    Article  Google Scholar 

  15. Agrawal, O.P.: A formulation and numerical scheme for fractional optimal control problems. J. Vib. Control 14, 1291–1299 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Baleanu, D., Defterli, O., Agrawal, O.P.: A central difference numerical scheme for fractional optimal control problems. J. Vib. Control 15, 583–597 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Agrawal, O.P., Defterli, O., Baleanu, D.: Fractional optimal control problems with several state and control variables. J. Vib. Control 16, 1967–1976 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, Y., Chen, Y.Q.: Fractional order linear quadratic regulator. In: IEEE/ASME International Conference on Mechtronic and Embedded Systems and Applications, pp. 363–368. (2008). doi:10.1109/MESA.2008.4735696

  19. Sierociuk, D., Vinagre, B.M.: Infinite horizon state-feedback LQR controller for fractional systems. In: 49th IEEE Conference on Decision and Control (CDC), pp. 6674–6679. (2010). doi:10.1109/CDC.2010.5717252

  20. Skogestad, S., Postlethwaite, I.: Multivariable Feedback Control: Analysis and Design, 2nd edn. Wiley, Hoboken (2005)

    MATH  Google Scholar 

  21. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    MATH  Google Scholar 

  22. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1998)

    MATH  Google Scholar 

  23. Farges, C., Moze, M., Sabatier, J.: Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 46, 1730–1734 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Matignon, D.: Stability results on fractional differential equations with applications to control processing. In: Computational Engineering in Systems Applications. Vol. 2. Lille, pp. 963–968 (1996)

  25. Merrikh-Bayat, F.: General formula for stability testing of linear systems with fractional-delay characteristic equation. Cent. Eur. J. Phys. 11, 855–862 (2013)

    Google Scholar 

  26. Diethelm, K., Ford, N.J., Freed, A.D.: A predictor–corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Merrikh-Bayat, F.: Fractional-order unstable pole-zero cancellation in linear feedback systems. J. Process Control 23, 817–825 (2013)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Zanjan, Zanjan, Iran

    Sara Hatamzadeh Arabi & Farshad Merrikh-Bayat

Authors
  1. Sara Hatamzadeh Arabi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farshad Merrikh-Bayat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sara Hatamzadeh Arabi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Arabi, S.H., Merrikh-Bayat, F. A Practical Method for Designing Linear Quadratic Regulator for Commensurate Fractional-Order Systems. J Optim Theory Appl 174, 550–566 (2017). https://doi.org/10.1007/s10957-017-1125-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-017-1125-0

Keywords

Mathematics Subject Classification

Search

Navigation