Three-stage ordered flow shops with either synchronous flow, blocking or no-idle machines | Journal of Scheduling Skip to main content
Springer Nature Link
Log in

Three-stage ordered flow shops with either synchronous flow, blocking or no-idle machines

  • Published:
Journal of Scheduling Aims and scope Submit manuscript

Abstract

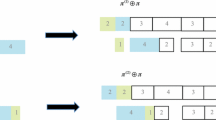
We show by induction that the shortest processing time sequence is optimal for a number of three-stage ordered flow shops with either synchronous flow, blocking or no-idle machines, effectively proving the optimality of an index priority rule when the adjacent job pairwise interchange argument does not hold. We also show that when the middle machine is maximal, the synchronous flow, blocking and no-wait problems are equivalent, because they can be effectively decomposed into two equivalent two-stage problems. A similar equivalence is shown for the classical flow shop and the flow shop with no-idle machines. These equivalences facilitate the solution of one problem by using the optimal algorithm for the equivalent problem. Finally, we observe that when the middle machine is minimal, the optimal sequence is not a pyramid sequence for the synchronous flow and blocking flow shops. On the other hand, we show that the optimal sequence for the flow shop with no-idle machines is a pyramid sequence obtainable by dynamic programming in pseudo-polynomial time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Adiri, I., & Pohoryles, D. (1982). Flow-shop/no-idle or no-wait scheduling to minimize the sum of completion times. Naval Research Logistics Quarterly,29, 495–504.

    Article  Google Scholar 

  • Allahverdi, A. (2016). A survey of scheduling problems with no-wait in process. European Journal of Operational Research,255, 665–686.

    Article  Google Scholar 

  • Arora, R. K., & Rana, S. R. (1980). Scheduling in a semi-ordered flow shop without intermediate queues. AIIE Trans,12, 263–272.

    Article  Google Scholar 

  • Axsater, S. (1982). On scheduling in a semi-ordered flow shop without intermediate queues. IIE Trans,14, 128–130.

    Article  Google Scholar 

  • Ding, J. Y., Song, S., Gupta, J. N., Wang, C., Zhang, R., & Wu, C. (2016). New block properties for flow shop scheduling with blocking and their application in an iterated greedy algorithm. International Journal of Production Research,54(16), 4759–4772.

    Article  Google Scholar 

  • Elmaghraby, S. E. (1968). The one machine sequencing problem with delay costs. Journal of Industrial Engineering,19, 105–108.

    Google Scholar 

  • Emmons, H., & Vairaktarakis, G. (2012). Flow shop scheduling: Theoretical results, algorithms, and application. Berlin: Springer.

    Google Scholar 

  • Goncharov, Y., & Sevastyanov, S. (2009). The flow shop problem with no-idle constraints: A review and approximation. European Journal of Operational Research,196, 450–456.

    Article  Google Scholar 

  • Hall, N. G., & Sriskandarajah, C. (1996). A survey of machine scheduling problems with blocking and no-wait in process. Operations Research,44, 510–525.

    Article  Google Scholar 

  • Hoo, S., & Hoogeveen, H. (2003). The three-machine proportionate flow shop problem with unequal machine speeds. Operations Research Letters,31, 225–231.

    Article  Google Scholar 

  • Johnson, S. M. (1954). Optimal two and three stage production schedules with setup times included. Naval Research Logistics Quarterly,1, 61–68.

    Article  Google Scholar 

  • Kalczynski, P. J., & Kamburowski, J. (2007). On no-wait and no-idle flow shops with makespan criterion. European Journal of Operational Research,178, 677–685.

    Article  Google Scholar 

  • Panwalkar, S. S., Smith, M. L., & Koulamas, C. (2013). Review of the ordered and proportionate flow shop scheduling research. Naval Research Logistics (NRL),60(1), 46–55.

    Article  Google Scholar 

  • Panwalkar, S. S., & Woollam, C. R. (1979). Flow shop scheduling problems with no in-process waiting: a special case. Journal of the Operational Research Society,30, 661–664.

    Article  Google Scholar 

  • Potts, C. N., & Strusevich, V. A. (2009). Fifty years of scheduling: A survey of milestones. Journal of the Operational Research Society,60, 541–568.

    Article  Google Scholar 

  • Smith, M. L., Panwalkar, S. S., & Dudek, R. A. (1975). Flow shop sequencing with ordered processing time matrices. Management Science,21, 544–549.

    Article  Google Scholar 

  • Smith, M. L., Panwalkar, S. S., & Dudek, R. A. (1976). Flow shop sequencing with ordered processing time matrices—A general case. Naval Research Logistics Quarterly,23, 481–486.

    Article  Google Scholar 

  • Soylu, B., Kica, O., & Azizoglu, M. (2007). Flow shop-sequencing problem with synchronous transfers and makespan minimization. International Journal of Production Research,45, 3311–3331.

    Article  Google Scholar 

  • Waldherr, S., & Knust, S. (2015). Complexity results for flow shop problems with synchronous movement. European Journal of Operational Research,242, 34–44.

    Article  Google Scholar 

Download references

Acknowledgements

We want to thank the reviewers, whose valuable critique helped us achieve greater clarity in the final version of the paper.

Author information

Authors and Affiliations

  1. Carey Business School, Johns Hopkins University, 100 International Drive, Baltimore, MD, 21202, USA

    S. S. Panwalkar

  2. Department of Information Systems and Business Analytics, Florida International University, Miami, FL, 33199, USA

    Christos Koulamas

Authors
  1. S. S. Panwalkar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Christos Koulamas
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Christos Koulamas.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Panwalkar, S.S., Koulamas, C. Three-stage ordered flow shops with either synchronous flow, blocking or no-idle machines. J Sched 23, 145–154 (2020). https://doi.org/10.1007/s10951-019-00618-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10951-019-00618-6

Keywords