Near-set Based Mucin Segmentation in Histopathology Images for Detecting Mucinous Carcinoma

Abstract

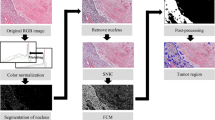
This paper introducesnear-set based segmentation method for extraction and quantification of mucin regions for detecting mucinouscarcinoma (MC which is a sub type of Invasive ductal carcinoma (IDC)). From histology point of view, the presence of mucin is one of the indicators for detection of this carcinoma. In order to detect MC, the proposed method majorly includes pre-processing by colour correction, colour transformation followed by near-set based segmentation and post-processing for delineating only mucin regions from the histological images at 40×. The segmentation step works in two phases such as Learn and Run.In pre-processing step, white balance method is used for colour correction of microscopic images (RGB format). These images are transformed into HSI (Hue, Saturation, and Intensity) colour space and H-plane is extracted in order to get better visual separation of the different histological regions (background, mucin and tissue regions). Thereafter, histogram in H-plane is optimally partitioned to find set representation for each of the regions. In Learn phase, features of typical mucin pixel and unlabeled pixels are learnt in terms of coverage of observed sets in the sample space surrounding the pixel under consideration. On the other hand, in Run phase the unlabeled pixels are clustered as mucin and non-mucin based on its indiscernibilty with ideal mucin, i.e. their feature values differ within a tolerance limit. This experiment is performed for grade-I and grade-II of MC and hence percentage of average segmentation accuracy is achieved within confidence interval of [97.36 97.70] for extracting mucin areas. In addition, computation of percentage of mucin present in a histological image is provided for understanding the alteration of such diagnostic indicator in MC detection.

APPENDIX

Start

for i=span_lower1 to span_upper1

t _i  = i

calculate ${\omega}_0=\sum \limits_{i=0}^{t_1-1}{p}_i$ and $-\sum \limits_{I=0}^{t_i-1}\frac{p_i}{\omega_0}\ \log\ \frac{p_i}{\omega_0}$

for j=span_lower2 to span_upper2

t ₂ = j

calculate ${\omega}_1=\sum \limits_{k={t}_1}^{t_2-1}{p}_k$ and $-\sum \limits_{k={t}_2}^{t_2-1}\frac{p_k}{\omega_1}\ \log\ \frac{p_k}{\omega_1}$

calculate ${\omega}_2=\sum \limits_{k={t}_2}^{t_{\mathrm{max}}}{p}_k$ and $-\sum \limits_{k={t}_2}^{t_{\mathrm{max}}}\frac{p_k}{\omega_2}\ \log\ \frac{p_k}{\omega_2}$

calculate entropy H(t) by Eq. 1.

Store H(t) and corresponding t ₁ and t ₂ value in a data structure.

end for

end for

Find index of max entropy and corresponding t ₁ and t ₂ at that index.

end