Entropy-TVD Scheme for the Shallow Water Equations in One Dimension | Journal of Scientific Computing
Skip to main content
Springer Nature Link
Log in

Entropy-TVD Scheme for the Shallow Water Equations in One Dimension

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

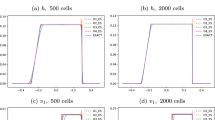
The Entropy-TVD scheme was developed for the non-linear scalar conservation laws in Chen and Mao (J Sci Comput 47:150–169, 2011). The scheme with step reconstruction simultaneously computes the two numerical entities, the numerical solution and the numerical entropy, and numerical examples show that the scheme provides a super-convergence rate. In this paper, we extend an Entropy-TVD scheme to the shallow water equations in one dimension. We prove that the scheme satisfies the entropy condition. Numerical tests show that the Entropy-TVD scheme has better resolution than the standard Godunov scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Chen, R., Mao, D.: Improved entropy-ultra-bee scheme for the Euler system of gas dynamics, J. Math. Comp. Accepted

  2. Chen, R., Mao, D.: Entropy-TVD scheme for nonlinear scalar conservation laws. J. Sci. Comput. 47, 150–169 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Chen, X., Nie, Y., Feng, J., Luo, X., Cai, L.: Self-adjusting entropy-stable scheme for compressible euler equations. Chin. Phys. B 24, 020202 (2015)

    Article  Google Scholar 

  4. Cui, Y., Mao, D.: Numerical method satisfying the first two conservation laws for the Korteweg-de Vries equation. J. Comput. Phys. 227, 376–399 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cui, Y., Mao, D.: Error self-canceling of a difference scheme maintaining two conservation laws for linear advection equation. Math. Comput. 81, 715–741 (2012)

    MathSciNet  MATH  Google Scholar 

  6. Fjordholm, U.S., Mishra, S., Tadmor, E.: Energy preserving and energy stable schemes for the shallow water equations equations. In: Cucker, F., Pinkus, A., Todd, M. (eds.) Foundations of Computational Mathematics, Proceedings of the FoCM Held in Hong Kong 2008, London Mathematical Society Lecture Notes Series, vol. 363, pp. 93–139 (2009)

  7. Fjordholm, U.S., Mishra, S., Tadmor, E.: Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 230, 5587–5609 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49, 357–393 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  9. Harten, A.: On the symmetric form of systems of conservation laws with entropy. J. Comput. Phys. 49, 151–164 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ismail, F., Roe, P.L.: Affordable, entropy-consistent Euler flux functions ii: entropy production at shocks. J. Comput. Phys. 228, 5410–5436 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. LeVeque, R.: Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge (2002)

    Book  MATH  Google Scholar 

  12. Li, H.: Entropy dissipating scheme for hyperbolic system of conservation laws in one space dimension. Doctoral Thesis, No. 11903-02820022

  13. Li, H., Wang, Z., Mao, D.: Numerically neither dissipative nor compressive scheme for linear advection equation and its application to the Euler system. J. Sci. Comput. 36, 285–331 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu, X., Osher, S.: Non-oscillatory high order accurate self similar maximum principle satisfying shock capturing schemes. SIAM J. Numer. Anal. 33, 760–779 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu, Y., Feng, J., Ren, J.: High resolution, entropy-consistent scheme using flux limiter for hyperbolic systems of conservation laws. J. Sci. Comput. 64, 914–937 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Roe, P.L.: Approximate riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43, 357–372 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  17. Tadmor, E.: Numerical viscosity of entropy stable schemes for systems of conservation laws. Math. Comput. 49, 91–103 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  18. Tadmor, E.: Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems. Acta Numer. 12, 451–512 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  19. Tadmor, E., Zhong, W.: Entropy stable approximations of navier-stokes equations with no artificial numerical viscosity. J. Hyperbolic Differ. Equ. 3, 529–559 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Toro, E.F.: Riemann problems and the waf method for solving the two-dimensional shallow water equations. Philos. Trans. Phys. Sci. Eng. 338, 43–68 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  21. Toro, E.F.: Shock-Capturing Methods for Free-Surface Shallow Flows. Wiley, Chichester (2001)

    MATH  Google Scholar 

  22. Wang, Z.: Finite difference schemes satisfying multiconservation laws for linear advection equations. Master’s Thesis, No. 11903-99118086

  23. Wang, Z.: Godunov type scheme satisfying two conservation laws. J. Fuyang Teach. Coll. (Nat. Sci.) 29, 22–26 (2012). (in Chinese)

    Google Scholar 

  24. Wang, Z., Mao, D.: Conservative difference scheme satisfying three conservation laws for linear advection equation. J. SHU 6, 588–598 (2006). (in Chinese)

    MATH  Google Scholar 

  25. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1999)

    Book  MATH  Google Scholar 

  26. Zhang, X., Shu, C.-W.: On maximum-principle-satisfying high order schemes for scalar conservation laws. J. Comput. Phys. 229, 3091–3120 (2010)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors wish to thank the referees for their valuable comments and suggestions, which really helped us in revising the paper. The research is supported by the National Natural Science Foundation of China Nos. 11201436, 11201435, and the Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan).

Author information

Authors and Affiliations

  1. School of Mathematics and Physics, China University of Geosciences, Wuhan, 430074, People’s Republic of China

    Rongsan Chen, Min Zou & Li Xiao

Authors
  1. Rongsan Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Min Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Rongsan Chen or Li Xiao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, R., Zou, M. & Xiao, L. Entropy-TVD Scheme for the Shallow Water Equations in One Dimension. J Sci Comput 71, 822–838 (2017). https://doi.org/10.1007/s10915-016-0322-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-016-0322-6

Keywords

Search

Navigation