Abstract
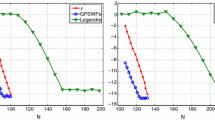
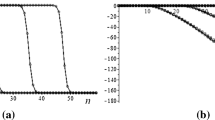
The prolate spheroidal wave equation (PSWE) is transformed, using suitable mappings, into three different canonical forms which resemble the Jacobi, Laguerre and the Hermite differential equations. The eigenpairs of the PSWE are approximated with the corresponding classical orthogonal polynomial as a basis set. It is observed that for any zonal wavenumber m the Jacobi type pseudospectral methods are well suited for small bandwidth parameters c whereas the Hermite and Laguerre pseudospectral methods are appropriate for very large c values. Moreover, Jacobi pseudospectral methods work well for any parameter values such that \(m\ge c\). Our numerical results confirm that for any values of m, the Jacobi \(\left[ (\alpha ,\beta )=(\pm 1/2,m)\right] \) and the Laguerre \(({\upgamma }=\pm 1/2)\) pseudospectral methods formulated in this article for the numerical solution of the PSWE with small and very large bandwidth parameters, respectively, are highly efficient both from the accuracy and fastness point of view.


Similar content being viewed by others
References
Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York (1970)
Alıcı, H., Taşeli, H.: Pseudospectral methods for an equation of hypergeometric type with a perturbation. J. Comput. Appl. Math. 234, 1140–1152 (2010)
Barakat, T., Abodayeh, K., Mukheimer, A.: The asymptotic iteration method for the angular spheroidal eigenvalues. J. Phys. A: Math. Gen. 38, 1299–1304 (2005)
Barrowes, B.E., O’Neill, K., Grzegorczyk, T.M., Kong, J.A.: On the asymptotic expansion of the spheroidal wave function and its eigenvalues for complex size parameter. Stud. Appl. Math. 113, 271–301 (2004)
Boyd, J.P.: Prolate spheroidal wave functions as an alternative to chebyshev and legendre polynomials for spectral element and pseudospectral algorithms. J. Comput. Phys. 199, 688–716 (2004)
Boyd, J.P.: Chebyshev and Fourier Spectral Methods, 2nd edn. Dover Publications Inc., Mineola (2001)
Boyd, J.P.: Prolate elements: prolate spheroidal wavefunctions as an alternative to Chebyshev and Legendre polynomials for spectral and pseudospectral algorithms. J. Comput. Phys. 199, 688–716 (2004)
Boyd, J.P.: Computation of grid points, quadrature weights and derivatives for spectral element methods using prolate spheroidal wave functions-prolate elements. ACM Trans. Math. Softw. 31, 149–165 (2005)
Chen, Q.Y., Gottlieb, D., Hesthaven, J.S.: Spectral methods based on prolate spheroidal wave functions for hyperbolic pdes. SIAM J. Numer. Anal. 43(5), 1912–1933 (2005)
Do-Nhat, T.: Asymptotic expansion of the Mathieu and prolate spheroidal eigenvalues for large parameter. Can. J. Phys. 77(8), 635–652 (1999)
Fang, Q., Nicholls, D.P., Shen, J.: A stable, high-order method for two-dimensional bounded-obstacle scattering. J. Comput. Phys. 224, 1145–1169 (2007)
Flammer, C.: Spheroidal Wave Functions. Stanford University Press, Stanford (1957)
Golub, G.H., Welsch, J.H.: Calculation of Gauss quadrature rules. Math. Comput. 23:221–230+s1–s10 (1969)
Hogan, J.A., Lakey, J.D.: Duration and Bandwidth Limiting: Prolate Functions. Sampling and Applications, Boston (2011)
Huang, Z., Xiao, J., Boyd, J.P.: Adaptive radial basis function and Hermite function pseudospectral methods for computing eigenvalues of the prolate spheroidal wave equation for very large bandwidth parameter. J. Comput. Phys. 281, 269–284 (2015)
Kong, W.Y., Rokhlin, V.: A new class of highly accurate differentiation schemes based on the prolate spheroidal wave functions. Appl. Comput. Harmon. Anal. 33(2), 226–260 (2012)
Nicholls, D.P., Reitich, F.: Analytic continuation of Dirichlet-Neumann operators. Numer. Math. 94(1), 107–146 (2003)
Ogburn, D.X., Waters, C.L., Sciffer, M.D., Hogan, J.A., Abbott, P.C.: A finite difference construction of the spheroidal wave functions. Comput. Phys. Commun. 185, 244–253 (2014)
Olver, F.W.J., Lozier, D.W., Boisvert, R.F. In: Clark, C.W. (ed.) NIST Handbook of Mathematical Functions. Press, Cambridge University (2010)
Osiov, A., Rokhlin, V., Xiao, H.: Prolate Spheroidal Wave Functions of Order Zero, vol. 187. Springer, New York (2013)
Schmutzhard, S., Hrycak, T., Feichtinger, H.G.: A numerical study of the Legendre-Galerkin method for the evaluation of the prolate spheroidal wave functions. Numer. Algorithms 68, 691–710 (2015)
Shen, J., Wang, L.L.: Fourierization of the Legendre-Galerkin method and a new space-time spectral method. Appl. Numer. Math. 57(5–7), 710–720 (2007)
Wang, L.L., Zhang, J., Zhang, Z.: On hp-convergence of prolate spheroidal wave functions and a new well-conditioned prolate-collocation scheme. J. Comput. Phys. 268, 377–398 (2014)
Weideman, J.A.C., Trefethen, L.N.: Eigenvalues of second-order spectral differentiation matrices. SIAM J. Numer. Anal. 25, 1279–1298 (1988)
Xiao, H., Rokhlin, V., Yarvin, N.: Prolate spheroidal wavefunctions, quadrature and interpolation. Inverse Probl. 17(4), 805–828 (2001)
Acknowledgements
The first author would like to dedicate this research to the memory of his father who suddenly passed away just two days later than the author’s arrival to USA. He feels a hearthfelt sadness for being thousands of miles away at the moment he passed away.The first author’s research was supported by a grant from TUBITAK, the Scientific and Technological Research Council of Turkey. The second author’s research was partially supported by NSF DMS-1419053 and AFOSR FA9550-16-1-0102.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alıcı, H., Shen, J. Highly Accurate Pseudospectral Approximations of the Prolate Spheroidal Wave Equation for Any Bandwidth Parameter and Zonal Wavenumber. J Sci Comput 71, 804–821 (2017). https://doi.org/10.1007/s10915-016-0321-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0321-7