A New Class of High-Order Energy Stable Flux Reconstruction Schemes for Triangular Elements | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

A New Class of High-Order Energy Stable Flux Reconstruction Schemes for Triangular Elements

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

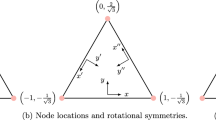
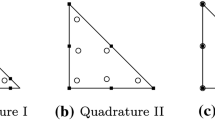
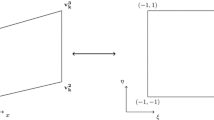
The flux reconstruction (FR) approach allows various well-known high-order schemes, such as collocation based nodal discontinuous Galerkin (DG) methods and spectral difference (SD) methods, to be cast within a single unifying framework. Recently, the authors identified a new class of FR schemes for 1D conservation laws, which are simple to implement, efficient and guaranteed to be linearly stable for all orders of accuracy. The new schemes can easily be extended to quadrilateral elements via the construction of tensor product bases. However, for triangular elements, such a construction is not possible. Since numerical simulations over complicated geometries often require the computational domain to be tessellated with simplex elements, the development of stable FR schemes on simplex elements is highly desirable. In this article, a new class of energy stable FR schemes for triangular elements is developed. The schemes are parameterized by a single scalar quantity, which can be adjusted to provide an infinite range of linearly stable high-order methods on triangular elements. Von Neumann stability analysis is conducted on the new class of schemes, which allows identification of schemes with increased explicit time-step limits compared to the collocation based nodal DG method. Numerical experiments are performed to confirm that the new schemes yield the optimal order of accuracy for linear advection on triangular grids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Carpenter, M.H., Kennedy, C.: Fourth-order 2n-storage Runge-Kutta schemes. Technical Report TM 109112, NASA, NASA Langley Research Center (1994)

  2. Castonguay, P., Liang, C., Jameson, A.: Simulation of transitional flow over airfoils using the spectral difference method. In: 40th AIAA Fluid Dynamics Conference, Chicago, IL, June 28–July 1 (2010). AIAA Paper, 2010-4626

    Google Scholar 

  3. Cockburn, B., Shu, C.W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comput. 52(186), 411–435 (1989)

    MathSciNet  MATH  Google Scholar 

  4. Cockburn, B., Shu, C.W.: The Runge-Kutta local projection P1-discontinuous Galerkin finite element method for scalar conservation laws. RAIRO Modél. Math. Anal. Numér. 25(3), 337–361 (1991)

    MathSciNet  MATH  Google Scholar 

  5. Cockburn, B., Shu, C.W.: Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. J. Sci. Comput. 16(3), 173–261 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cockburn, B., Lin, S.Y., Shu, C.W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84(1), 90–113 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cockburn, B., Hou, S., Shu, C.W.: The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV: The multidimensional case. Math. Comput. 54(190), 545–581 (1990)

    MathSciNet  MATH  Google Scholar 

  8. Dubiner, M.: Spectral methods on triangles and other domains. J. Sci. Comput. 6(4), 345–390 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hesthaven, J.S., Warburton, T.: Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer, Berlin (2007)

    Google Scholar 

  10. Huynh, H.T.: A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods. In: 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, Jun 25–28 (2007). AIAA Paper, 4079

    Google Scholar 

  11. Huynh, H.T.: A reconstruction approach to high-order schemes including discontinuous Galerkin for diffusion. In: 47th AIAA Aerospace Sciences Meeting, Orlando, FL, Jan 5–8 (2009). AIAA Paper, 403

    Google Scholar 

  12. Jameson, A.: A proof the stability of the spectral difference method for all orders of accuracy. J. Sci. Comput. 45(1–3), 348–358 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kannan, R., Wang, Z.J.: A study of viscous flux formulations for a p-multigrid spectral volume Navier Stokes solver. J. Sci. Comput. 41(2), 165–199 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kannan, R., Wang, Z.J.: LDG2: A variant of the LDG flux formulation for the spectral volume method. J. Sci. Comput. 46(2), 314–328 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kopriva, D.A., Kolias, J.H.: A conservative staggered-grid Chebyshev multidomain method for compressible flows. J. Comput. Phys. 125, 244–261 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  16. Liang, C., Kannan, R., Wang, Z.J.: A p-multigrid spectral difference method with explicit and implicit smoothers on unstructured triangular grids. Comput. Fluids 38, 254–265 (2009)

    Article  MathSciNet  Google Scholar 

  17. Liu, Y., Vinokur, M., Wang, Z.J.: Spectral difference method for unstructured grids i: Basic formulation. J. Comput. Phys. 216, 780–801 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Raviart, P.A., Thomas, J.M.: A mixed hybrid finite element method for the second order elliptic problems. In: Mathematical Aspects of the Finite Element Method. Lectures Notes in Mathematics. Springer, Berlin (1977)

    Google Scholar 

  19. Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Los Alamos Report LA-UR-73-479 (1973)

  20. Roe, P.L.: Approximate Riemann solvers, parameter vectors and difference schemes. J. Comput. Phys. 43, 357–372 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  21. Van den Abeele, K., Lacor, C., Wang, Z.J.: On the stability and accuracy of the spectral difference method. J. Sci. Comput. 37(2), 162–188 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Vincent, P.E., Castonguay, P., Jameson, A.: A new class of high-order energy stable flux reconstruction schemes. J. Sci. Comput. 47(1), 50–72 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  23. Wang, Z.J., Gao, H.: A unifying lifting collocation penalty formulation including the discontinuous Galerkin, spectral volume/difference methods for conservation laws on mixed grids. J. Comput. Phys. 228(21), 8161–8186 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wang, Z.J., Liu, Y., May, G., Jameson, A.: Spectral difference method for unstructured grids II: Extension to the Euler equations. J. Sci. Comput. 32, 45–71 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhang, M., Shu, C.W.: An analysis of three different formulations of the discontinuous Galerkin method for diffusion equations. Math. Models Methods Appl. Sci. 13(3), 395–414 (2003)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aeronautics and Astronautics, Stanford University, Stanford, CA, 94305, USA

    P. Castonguay, P. E. Vincent & A. Jameson

Authors
  1. P. Castonguay
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. E. Vincent
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Jameson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. Castonguay.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Castonguay, P., Vincent, P.E. & Jameson, A. A New Class of High-Order Energy Stable Flux Reconstruction Schemes for Triangular Elements. J Sci Comput 51, 224–256 (2012). https://doi.org/10.1007/s10915-011-9505-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-011-9505-3

Keywords

Search

Navigation