Nodal Superconvergence of SDFEM for Singularly Perturbed Problems | Journal of Scientific Computing Skip to main content
Springer Nature Link
Log in

Nodal Superconvergence of SDFEM for Singularly Perturbed Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

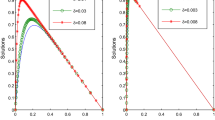
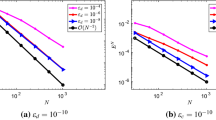
In this paper, we analyze the streamline diffusion finite element method for one dimensional singularly perturbed convection-diffusion-reaction problems. Local error estimates on a subdomain where the solution is smooth are established. We prove that for a special group of exact solutions, the nodal error converges at a superconvergence rate of order (ln ε −1/N)2k (or (ln N/N)2k) on a Shishkin mesh. Here ε is the singular perturbation parameter and 2N denotes the number of mesh elements. Numerical results illustrating the sharpness of our theoretical findings are displayed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Brenner, P., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15. Springer, Berlin (1994)

    MATH  Google Scholar 

  2. Celiker, F., Cockburn, B.: Element-by-element post-processing of discontinuous Galerkin methods for Timoshenko beams. J. Sci. Comput. 27(1–3), 177–187 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  3. Celiker, F., Cockburn, B.: Superconvergence of the numerical traces of discontinuous Galerkin and hybridized methods for convection-diffusion problems in one space dimension. Math. Comput. 76(257), 67–96 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  4. Chen, L., Xu, J.: An optimal streamline diffusion finite element method for a singularly perturbed problem. In: Recent Advances in Adaptive Computation. Contemp. Math., vol. 383, pp. 191–201. Am. Math. Soc., Providence (2005)

    Google Scholar 

  5. Chen, L., Xu, J.: Stability and accuracy of adapted finite element methods for singularly perturbed problems. Numer. Math. 109, 167–191 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  6. Ciarlet, P.: The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978)

    MATH  Google Scholar 

  7. Guzmán, J.: Local analysis of discontinuous Galerkin methods applied to singularly perturbed problems. J. Numer. Math. 14(1), 41–56 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  8. Hughes, T.J.R., Brooks, A.: A multidimensional upwind scheme with no crosswind diffusion. In: Finite element methods for convection dominated flows (Papers, Winter Ann. Meeting Amer. Soc. Mech. Engrs., New York, 1979). AMD, vol. 34, pp. 19–35. Am. Soc. Mech. Engrs. (ASME), New York (1979)

    Google Scholar 

  9. Johnson, C., Schatz, A.H., Wahlbin, L.B.: Crosswind smear and pointwise errors in streamline diffusion finite element methods. Math. Comput. 49(179), 25–38 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  10. Douglas, J. Jr., Dupont, T.: Galerkin approximations for the two point boundary problem using continuous, piecewise polynomial spaces. Numer. Math. 22, 99–109 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  11. Miller, J.H.H., O’Riordan, E., Shishkin, G.I.: Fitted Numerical Methods for Singular Perturbation Problems. World Scientific, Singapore (1996)

    MATH  Google Scholar 

  12. Roos, H.-G.: Layer-adapted grids for singular perturbation problems. ZAMM Z. Angew. Math. 78, 291–309 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  13. Roos, H.-G., Stynes, M., Tobiska, L.: Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion and Flow Problems. Springer, Berlin (1996)

    MATH  Google Scholar 

  14. Stynes, M.: Steady-State Convection-Diffusion Problems. Acta Numerica, vol. 14, pp. 445–508. Cambridge University Press, Cambridge (2005)

    Google Scholar 

  15. Stynes, M.: Convection-diffusion-reaction problems, SDFEM/SUPG and a priori meshes. Int. J. Comput. Sci. Math. 1(2–4), 412–431 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  16. Stynes, M., Tobiska, L.: Using rectangular Q p elements in the SDFEM for a convection-diffusion problem with a boundary layer. Appl. Numer. Math. 58(12), 1789–1802 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  17. Tobiska, L.: Analysis of a new stabilized higher order finite element method for advection-diffusion equations. Comput. Methods Appl. Mech. Eng. 196(1–3), 538–550 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  18. Xie, Z., Zhang, Z.: Superconvergence of DG method for one-dimensional singularly perturbed problems. J. Comput. Math. 25(2), 185–200 (2007)

    MATH  MathSciNet  Google Scholar 

  19. Xie, Z., Zhang, Z.: Uniform superconvergence analysis of the discontinuous Galerkin method for a singularly perturbed problem in 1-D. Math. Comput. 79(269), 35–45 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  20. Xie, Z., Zhang, Z., Zhang, Z.: A numerical study of uniform superconvergence of LDG method for solving singularly perturbed problems. J. Comput. Math. 27(2)

  21. Zhang, Z.: Finite element superconvergence approximation for one-dimensional singularly perturbed problems. Numer. Methods Partial Differ. Equ. 18(3), 374–395 (2002)

    Article  MATH  Google Scholar 

  22. Zhu, H.: Discontinuous Galerkin methods for singularly perturbed problems. Ph.D. thesis, Wayne State University, Detroit (2009)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Wayne State University, Detroit, MI, 48202, USA

    Fatih Celiker & Zhimin Zhang

  2. Department of Mathematics, The University of Southern Mississippi, Hattiesburg, MS, 39406, USA

    Huiqing Zhu

Authors
  1. Fatih Celiker
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhimin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huiqing Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huiqing Zhu.

Additional information

Part of this work was done when the first author was a long-term visitor at the Institute for Mathematics and its Applications (IMA), University of Minnesota, MN, during the Fall semester of 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Celiker, F., Zhang, Z. & Zhu, H. Nodal Superconvergence of SDFEM for Singularly Perturbed Problems. J Sci Comput 50, 405–433 (2012). https://doi.org/10.1007/s10915-011-9489-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-011-9489-z

Keywords

Search

Navigation