The effect of vertex and edge deletion on the edge metric dimension of graphs

Abstract

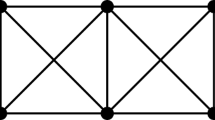
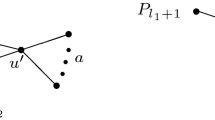
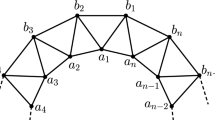
Let $G=(V(G),E(G))$ be a connected graph. A set of vertices $S\subseteq V(G)$ is an edge metric generator of G if any pair of edges in G can be distinguished by their distance to a vertex in S. The edge metric dimension edim(G) is the minimum cardinality of an edge metric generator of G. In this paper, we first give a sharp bound on $edim(G-e)-edim(G)$ for a connected graph G and any edge $e\in E(G)$. On the other hand, we show that the value of $edim(G)-edim(G-e)$ is unbounded for some graph G and some edge $e\in E(G)$. However, for a unicyclic graph H, we obtain that $edim(H)-edim(H-e)\le 1$, where e is an edge of the unique cycle in H. And this conclusion generalizes the result on the edge metric dimension of unicyclic graphs given by Knor et al. Finally, we construct graphs G and H such that both $edim(G)-edim(G-u)$ and $edim(H-v)-edim(H)$ can be arbitrarily large, where $u\in V(G)$ and $v\in V(H)$.