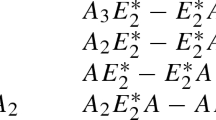Abstract
If s is an even power of a prime and t equals s or \(s\sqrt{s}\), we show the existence of pseudo-geometric strongly regular graphs having the same parameters of the point-graph of a GQ(s, t), that are not geometric.
Similar content being viewed by others
References
Barwick S.G., Ai Jackson W., Penttila T.: New families of strongly regular graphs. Preprint arXiv:1606.05380.
Coolsaet K., Degraer J., Spence E.: The strongly regular \((45,12,3,3)\) graphs. Electron. J. Comb. 13(1), R32 (2006).
Cossidente A., Pavese F.: On the geometry of unitary involutions. Finite Fields Appl. 36, 14–28 (2015).
Fon-Der-Flaass D.G.: New prolific constructions of strongly regular graphs. Adv. Geom. 2, 301–306 (2002).
Godsil C.D., McKay B.D.: Constructing cospectral graphs. Aequationes Math. 25, 257–268 (1982).
Haemers W.H., Spence E.: The pseudo-geometric graphs for generalized quadrangles of order \((3, t)\). Eur. J. Comb. 22(6), 839–845 (2001).
Hui A.M.W., Rodrigues B.: Switched graphs of some strongly regular graphs related to the symplectic graph. Preprint arXiv:1605.07400.
Ihringer F.: A switching for all strongly regular collinearity graphs from polar spaces. Preprint arXiv:1606.05898.
Kantor W.M.: Strongly regular graphs defined by spreads. Israel J. Math. 41, 298–312 (1982).
Lane-Harvard E.: New constructions of strongly regular graphs. Ph.D. Thesis, Colorado State University (2014).
Muzychuk M.: A generalization of Wallis–Fon-Der-Flaass construction of strongly regular graph. J. Algebr. Comb. 25, 169–187 (2007).
Payne S.E., Thas J.A.: Finite Generalized Quadrangles. Research Notes in Mathematics, vol. 110. Pitman, Boston (1984).
Segre B.: Forme e geometrie hermitiane con particolare riguardo al caso finito. Ann. Mat. Pura Appl. 70, 1–201 (1965).
Spence E.: The strongly regular \((40,12,2,4)\) graphs. Electron. J. Comb. 7, R22 (2000).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by D. Ghinelli.
Rights and permissions
About this article
Cite this article
Cossidente, A., Pavese, F. Strongly regular graphs from classical generalized quadrangles. Des. Codes Cryptogr. 85, 457–470 (2017). https://doi.org/10.1007/s10623-016-0318-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-016-0318-0