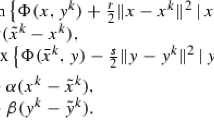An alternating extragradient method with non euclidean projections for saddle point problems | Computational Optimization and Applications Skip to main content
Springer Nature Link
Log in

An alternating extragradient method with non euclidean projections for saddle point problems

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

In this work we analyze a first order method especially tailored for smooth saddle point problems, based on an alternating extragradient scheme. The proposed method is based on three successive projection steps, which can be computed also with respect to non Euclidean metrics. The stepsize parameter can be adaptively computed, so that the method can be considered as a black-box algorithm for general smooth saddle point problems. We develop the global convergence analysis in the framework of non Euclidean proximal distance functions, under mild local Lipschitz conditions, proving also the \(\mathcal {O}(\frac{1}{k})\) rate of convergence on the primal–dual gap. Finally, we analyze the practical behavior of the method and its effectiveness on some applications arising from different fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Bonettini, S., Ruggiero, V.: An alternating extragradient method for total variation based image restoration from Poisson data. Inverse Probl. 27, 095001 (2011)

    Article  MathSciNet  Google Scholar 

  2. Korpelevich, G.: The extragradient method for finding saddle points and other problems. Ekonomika i Matematicheskie Metody 12, 747–756 (1976)

    MATH  MathSciNet  Google Scholar 

  3. Nemirovski, A.: Prox-method with rate of convergence \(\cal O\)(1/t) for variational inequalities with Lipschitz continuous monotone operators and smooth convex–concave saddle point problems. SIAM J. Optim. 15(1), 229–251 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  4. Auslender, A., Teboulle, M.: Interior projection-like methods for monotone variational inequalities. Math. Program. Ser. A 104, 39–68 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  5. Auslender, A., Teboulle, M.: Projected subgradient methods with non-euclidean distances for non-differentiable convex minimization and variational inequalities. Math. Program. Ser. B 120, 27–48 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  6. Juditsky, A., Nemirovski, A.: First Order Methods for Nonsmooth Convex Large-Scale Optimization, I: General Purpose Methods, pp. 1–28. The MIT Press, Cambridge (2011)

    Google Scholar 

  7. Juditsky, A., Nemirovski, A.: First Order Methods for Nonsmooth Convex Large-Scale Optimization, II: Utilizing Problem Structure, pp. 29–63. The MIT Press, Cambridge (2011)

    Google Scholar 

  8. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  9. Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Program. Ser. A 103, 127–152 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  10. Patriksson, M.: Nonlinear Programming and Variational Inequality Problems: a Unified Approach. Kluwer Academic Publisher, Dordrecht (1999)

    Book  MATH  Google Scholar 

  11. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)

    MATH  Google Scholar 

  12. Khobotov, E.N.: Modification of the extragradient method for solving variational inequalities and certain optimization problems. USSR Comput. Math. Phys. 27, 120–127 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  13. Marcotte, P.: Application of Khobotov’s algorithm to variational inequalities and network equilibrium problems. INFOR. 29, 258–270 (1991)

    MATH  Google Scholar 

  14. Antipin, A.S.: From optima to equilibria. In: Dynamics of non-homogeneous systems. Proceedings of ISA-RAS (2000).

  15. Antipin, A.S.: Feedback-controlled saddle gradient processes. Autom. Remote Control 55(3), 311–320 (2003)

    MathSciNet  Google Scholar 

  16. Censor, Y., Iusem, A.N., Zenios, S.A.: An interior point method with Bregman functions for the variational inequality problem with paramonotone operators. Math. Program. 81, 373–400 (1998)

    MATH  MathSciNet  Google Scholar 

  17. Arrow, K.J., Hurwicz, L., Uzawa, H.: Studies in Linear and Non-Linear Programming. Stanford University Press, Stanford (1958)

    MATH  Google Scholar 

  18. Bonettini, S., Ruggiero, V.: On the convergence of primal-dual hybrid gradient algorithms for total variation image restoration. J. Math. Imaging Vis. (2012). doi:10.1007/s10851-011-0324-9

  19. Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM J. Optim. 3, 538–543 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  20. Beck, A., Teboulle, M.: Mirror descent and nonlinear projected subgradient methods for convex optimization. Oper. Res. Lett. 31, 167–175 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  21. Zanella, R., Boccacci, P., Zanni, L., Bertero, M.: Efficient gradient projection methods for edge-preserving removal of Poisson noise. Inverse Probl. 25, 045010 (2009)

    Article  MathSciNet  Google Scholar 

  22. Dai, Y.H., Fletcher, R.: New algorithms for singly linearly constrained quadratic programs subject to lower and upper bounds. Math. Program. Ser. A 106, 403–421 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  23. Le, T., Chartrand, R., Asaki, T.J.: A variational approach to reconstructing images corrupted by Poisson noise. J. Math. Imaging Vis. 27, 257–263 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work has been supported by MIUR (Italian Ministry for University and Research), under the projects PRIN 2008, contract 2008T5KA4L and FIRB—Futuro in Ricerca 2012, contract RBFR12M3AC.

Author information

Authors and Affiliations

  1. Dipartimento di Matematica e Informatica, Università di Ferrara, Polo Scientifico Tecnologico, Blocco B, Via Saragat 1, 44122 , Ferrara, Italy

    Silvia Bonettini & Valeria Ruggiero

Authors
  1. Silvia Bonettini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Valeria Ruggiero
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Valeria Ruggiero.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bonettini, S., Ruggiero, V. An alternating extragradient method with non euclidean projections for saddle point problems. Comput Optim Appl 59, 511–540 (2014). https://doi.org/10.1007/s10589-014-9650-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-014-9650-3

Keywords

Search

Navigation